Технические науки/10.Горное дело

Профессор Адырбеков М.А., к.т.н. Каражанов А.А.

Таразский государственный университет имени М.Х.Дулати,

Республика Казахстан

СПОСОБ ПОЛУЧЕНИЯ КРИВЫХ 4-ГО ПОРЯДКА С ИСПОЛЬЗОВАНИЕМ ГЕОМЕТРИЧЕСКОГО ПРЕОБРАЗОВАНИЯ Д₂

Одним из основных направлений исследования начертательной геометрии является развитие теории геометрических преобразований с целью применения в решении научных и технических задач, связанных сложными геометрическими формами.

В шахтном строительстве часто применяется каналовые поверхности сводчатой формы. Сводчатая форма более благоприятна с точки зрения ее устойчивости, рационального использования крепи, ее несущей способности и перераспределения воспринимающих ею нагрузок. При проектировании горизонтальных выработок возникает вопрос геометрического конструирования поверхности сводов. На практике используются, в основном, составные своды из дуг кривых 2-го порядка или сплайны, что усложняют решения конструкторских и технологических задач.

Для формообразования криволинейных поверхностей подземных выработок можно использовать геометрические преобразования, в частности (2-2)-значные преобразования, что позволяет моделировать сложные поверхности по наперед заданным геометрическим параметрам и автоматизировать процесс их проектирования. Поэтому, разработка рациональных способов и алгоритмов геометрического моделирования сложных поверхностей подземных выработок является актуальной задачей.

В данной научной статье излагается формообразование кривых 4-го порядка с применением преобразования Д₂, когда прообразом представляет собой окружность, который на плоскости имеет различные расположения.

В общем случае каждая точка окружности m преобразуется в четыре точки плоскости. Множесто точек окружности m отображается в кривую 4-го порядка m^' с использованием преобразования Д₂. Уравнение кривой m^' определяется следующим образом:

· Уравнение прообраза m запишем в виде:

, (1)

где х, у – координаты точек прообраза;

с, d, r – постоянные коэффициенты.

· Уравнения (2-2)-значного преобразования Д₂ пишется в виде:

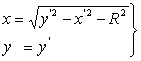, (2)

где ,- координаты точки-образа;

x, y – координаты точки-прообраза;

R – параметр преобразования.

· Значения х и у из системы уравнении 2 подставив в уравнение 1 , получим уравнение кривой m^' в виде:

, (3)

где х^' и у^' – координаты точек образа;

с, d, r – постоянные прообраза;

R – параметр преобразования Д₂.

Рассмотрим примеры отображения прообраза m в образ m^' с применением преобразования Д₂.

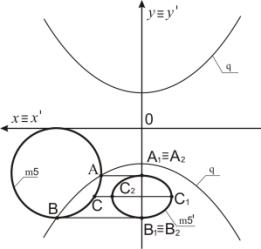
Пример 1. На рисунке 1 задан прообраз m5. Точка А преобразуется в точку А₁ ≡ А₂. Точка С отображается в две точки С₁ и С₂. Точка В проебразуется в точки В₁ и В₂. Окружность m5 преобразуется в кривую 2-го порядка m5^'.

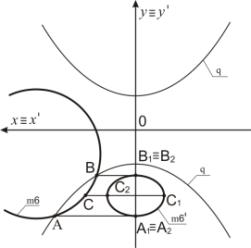
Пример 2. На рисунке 2 задана окружность m6. Точка В преобразуется в точку В₁ ≡ В₂. Точка С отображается в точку С₁ ≡ С₂. Точка А преобразуется в точку А₁ ≡ А₂. Окружность m6 преобразуется в кривую 2-го порядка m6^' (рисунок 2).

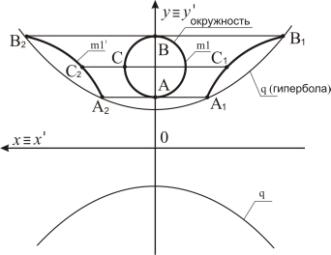
Пример 3. Точки прообраза m1 (рисунок 3) подвергаем преобразованию Д₂. Точка А преобразуется в точки А₁ и А₂. Точка В отображается в точки В₁ и В₂. Точка С преобразуется в точки С₁ и С₂. Прообраз m1 преобразуется в две кривые 2-го порядка m1^'.

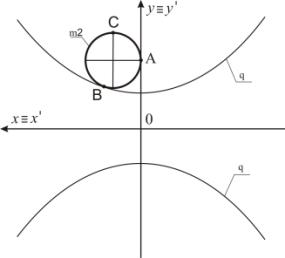
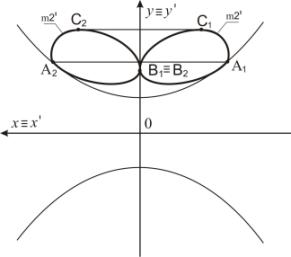
Пример4. На рисунке 4 задан прообраз m2. Точка А преобразуется в точки А₁ и А₂. Точка В отображается в точку В₁ = В₂. Точка С преобразуется в точки С₁ и С₂. Окружность m2 преобразуется в две кривые 2-го порядка m2^' (рисунок 5).

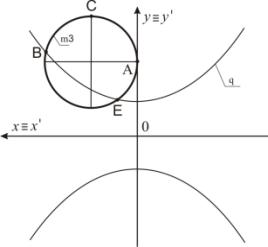
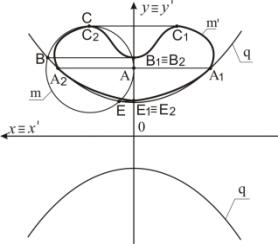
Пример 5. На рисунке 6 задана окружность m3. Точка А преобразуется в точки А₁ и А₂. Точка В отображается в точку В₁ ≡ В₂. Точка Е преобразуется в точку Е₁ ≡ Е₂. Точка С преобразуется в точки С₁ и С₂. Прообраз m3 преобразуется в кривую 4-го порядка m3^' (рисунок 7).

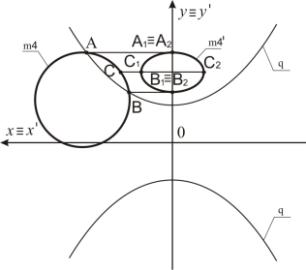
Пример 6. На рисунке 8 задана окружность m4. Точка А преобразуется в точку А₁ ≡ А₂ с использованием преобразования Д₂. Точка В отображается в точку В₁ ≡ В₂. Точка С преобразуется в точки С₁ и С₂. Прообраз m4 преобразуется в кривую 2-го порядка m4^' (рисунок 8).

Рассмотренные в статье множество примеров показывает характер изменения формы образа (кривой 4-го порядка), когда прообраз занимает различные положения на плоскости. Выявленные свойства геометрического преобразования Д₂ позволяют их использовать в решении прикладных задач начертательной геометрии.

Предложенный способ позволяет конструировать гладкую геометрическую форму переходных участков поверхностей подземных выработок, получить ее уравнение и профилировать полученную поверхность на персональном компьютере, что облегчает работу горного инженера.

Рисунок 1 – Преобразование прообраза m5	Рисунок 2 – Преобразование прообраза m6
Рисунок 3 – Преобразование прообраза m1
Рисунок 4 – Заданный прообраз m2	Рисунок 5 – Полученный образ m2^'
Рисунок 6 – Заданный прообраз m3	Рисунок 7 – Полученный образ m3^'
Рисунок 8 – Преобразование прообраза m4

Литература

1 . Михайленко В.Е., Кислокий А.А. и др. Геометрическое моделирование и машинная графика. – Киев.: Вища школа, 1991. - 373с.

2 . Нурмаханов Б.Н., Усупов М.М. Разработка способа задания (1-4)- значных преобразований и их применение в построении кривых. – Алматы: Поиск, 1997. - №1.

3 . Байдабеков А.К. Теория нелинейных преобразований и их применение в науке и технике: автореф. … докт. техн. наук:.05.01.01. – М., 2006. – 36с.

4 . Усупов М.М. Разработка и применение (1-4) – значных геометрических преобразований специального вида: автореф. … канд. техн. наук:.05.01.01. – Алматы: КазНТУ, 2004. – 16 с.