Технические науки/10.Горное
дело
Каражанов А.А.
Таразский
государственный университет имени М.Х.Дулати,
Республика
Казахстан
МЕТОД ФОРМООБРАЗОВАНИЯ КРИВЫХ 4-ГО ПОРЯДКА С ИСПОЛЬЗОВАНИЕМ (2-2)-ЗНАЧНОГО ПРЕОБРАЗОВАНИЯ Г2
Данная
статья посвящена получению новых кривых
4-го порядка с применением (2-2)-значного
геометрического
преобразования
Г2, когда прообразом является эллипс различного расположения на плоскости.
Преобразование эллипса
В
общем случае преобразование Г2 преобразует эллипс n
в кривую 4-го порядка n',
уравнение которой может быть определено в следующей последовательности:
1) уравнение
(2-2)-значного преобразования Г2 пишется в виде:
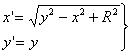 , (1)
, (1)
где x,y – координаты
точки-прообраза;
x',y' – координаты точки-образа;
R – постоянное число, R>0.
2) из системы уравнений (1)
можно определить уравнения обратного
(2-2)-значного преобразования Г'2 в виде:
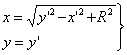 , (2)
, (2)
где x,y– координаты
точки-прообраза;
x',y' – координаты точки-образа;
R – постоянное число R>0.
3)
записывается уравнение эллипса n в
виде
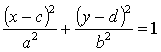 , (3)
, (3)
4)
из системы уравнений (2) значения x
и y подставив в уравнение (3), получим уравнение образа n' в виде
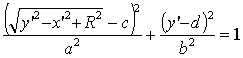 , (4)
, (4)
где x', y' – координаты точек кривой n';
c, d –
параметры прообраза n;
R – параметр преобразования Г2.
Рассмотрим
примеры преобразования эллипса n в
различные кривые образы.
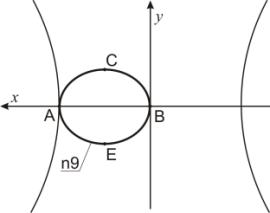
Пример 1. На рисунке 1 задан эллипс n9,
горизонтальная ось АВ которого инцидентна оси Ох. При этом точка А расположена на граничной кривой ℓ и точка В расположена в начале координат. Точка А отображается в точку А1≡А2 преобразованием Г2. Точка В преобразуется в две
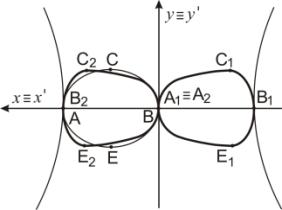
точки В1
и В2. Точка
Е преобразуется в точки Е1 и Е2.
Эллипс n9 преобразуется в две
кривые 2-го порядка n9'
(рисунок 2).
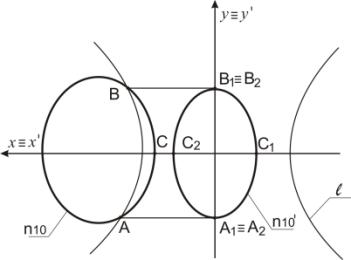
Пример 2. На рисунке 3 задан эллипс n10,
центр которого расположен на оси Ох.
Точка В отображается в точку В1≡В2 с использованием преобразования Г2.
Точка С преобразуется в точки С1 и С2.
Точка А отображается в точку А1≡А2.
Эллипс
n10 преобразуется в кривую
2-го порядка n10'
(рисунок 3).
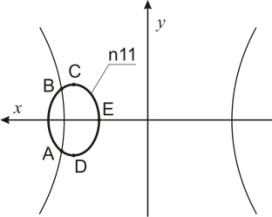
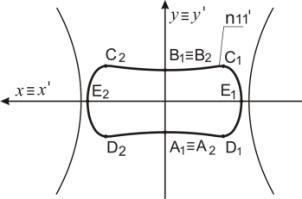
Пример 3. На рисунке 4 задан эллипс n11,
центр которого расположен в области определения преобразования Г2.
Точка В отображается в точку В1≡В2 преобразованием Г2. Точка А преобразуется в точку А1≡А2. Точка С отображается в две точки С1 и С2. Точка D
преобразуется в две точки D1 и D2. Точка
E отображается в точки Е1 и Е2. Эллипс n11 преобразуется в кривую 4-го порядка n11' (рисунок 5).
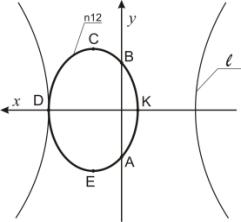
Пример 4. На рисунке 6 задан эллипс n12, который пересекает ось Оy в точках А и В. Точка В отображается в две
точки В1 и В2 преобразованием Г2. Точка D преобразуется в точку D1≡ D2. Точка
А
преобразуется в две точки А1 и А2. Точка
K отображается в точки K1 и K2. Эллипс
n12 преобразуется в две кривые n12' (рисунок 7).
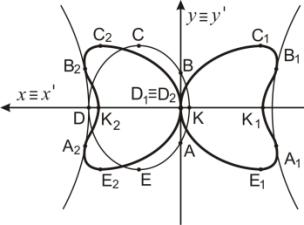
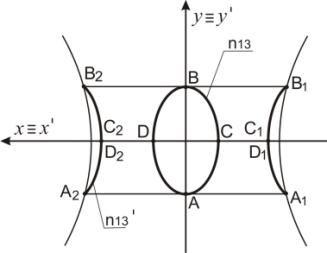
Пример 5. На рисунке 8
центр эллипса n13 расположен в начале
координат. Эллипс
n13 преобразуется в две
кривые n13' (рисунок 8). При этом точка B
отображается в точки В1 и В2, точка С – в
точки С1 и С2, точка D – в точки D1 и D2.
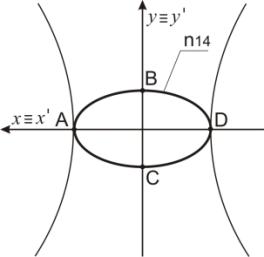
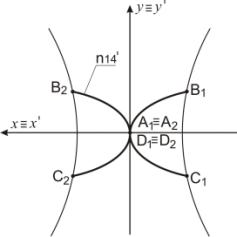
Пример 6. На рисунке 9 задан эллипс n14,
большая ось АD которого расположен на оси Оx. Точка В преобразуется в точки В1 и В2,
точка С – в точки С1 и С2, точка А - в точку А1≡А2,
точка D – в точку D1≡D2. Эллипс n14 преобразуется в две кривые n14' (рисунок 10).
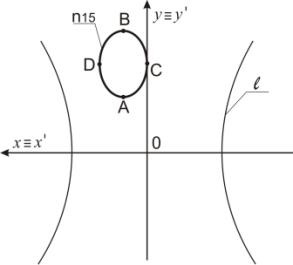
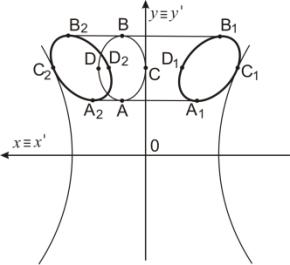
Пример 7. На рисунке 11 заданный эллипс n15
касается с осью Оy. Точка В преобразуется
в точки В1 и В2, точка С – в точки С1 и С2, точка А - в точки А1 и А2, точка D –
в точки D1 и D2. Эллипс
n15 преобразуется в две кривые n15' (рисунок 12).
Примеры, рассмотренные выше, показывают как
изменяется форма кривой-образа в зависимости от расположения эллипса на
плоскости и от его размеров. Преобразование кривых второго порядков с
использованием преобразования Г2 позволило получить новые кривые
4-го порядка, что расширяет существующие границы знаний о теории плоских
кривых.
|
Рисунок
1 - Задание
прообраза n9 |
Рисунок
2 - Полученный
образ n9’ |
|
Рисунок
3 - Преобразование прообраза n10 |
|
|
Рисунок 4 - Задание прообраза n11 |
Рисунок
5 - Полученный
образ n11’ |
|
Рисунок 6 - Задание прообраза n12 |
Рисунок
7 - Полученный
образ n12’ |
|
Рисунок
8 - Преобразование прообраза n13 |
|
|
Рисунок 9 - Задание прообраза n14 |
Рисунок
10 - Полученный
образ n14’ |
|
Рисунок 11 - Задание прообраза n15 |
Рисунок
12 - Полученный
образ n15’ |
Литература
1 Ермаков А.В. Кремоновы преобразования
пространства в конструиро-вании рациональных каркасных поверхностей: автореф.
...канд.техн.наук:. 05.01.01. – М.: МТИПП, 1977. – 17 с.
2 Завьялов Ю.С.,Леус В.А., Скороспелов В.А.
Сплайны в инженерной геометрии. - М.: Машиностроение, 1985. – 222 с.
3 Конакбаев К.К. Конструирование обводов
из дуг уникурсальных циркулярных кривых посредством кремоновых инволюций.
автореф. ...канд.техн.наук:.05.150. – М.: МТИПП, 1972. – 18 с.
4 Котов И.И. Алгоритмы конструирования
каркасных поверхностей. – М.: МАИ, 1975.
5 Манеевич В.А. К теории многозначных
точечных соответствий // Труды МИИТ: Вопросы дифференциальной, синтетической
прикладной геометрии. – М.: 1965, №190. – С.158-160.
6
Фролов С.А. Методы преобразования ортогональных проекций. – М.: Машиностроение,
1970. – 160 с.