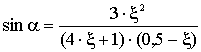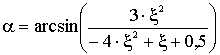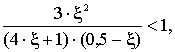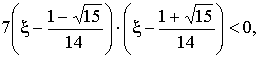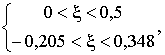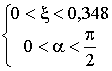К.т.н. Волков В.П.,
к.т.н. Земцова О.Г., Волкова О.В.
Пензенский
государственный университет архитектуры и строительства, Россия
Определение диапазон изменения
относительной длины свеса полки Z-образного профиля
Рассмотрим тонкостенный стержень с Z-образным
профилем (рис. 1), принимаем толщину 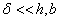 . Вычисление
основных геометрических характеристик поперечного сечения в практических
расчетах можно существенно упростить, если ввести безразмерный коэффициент
ξ, характеризующий отношение длины свеса полки к полной длине профиля:
. Вычисление
основных геометрических характеристик поперечного сечения в практических
расчетах можно существенно упростить, если ввести безразмерный коэффициент
ξ, характеризующий отношение длины свеса полки к полной длине профиля:
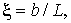
где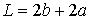 – полная длина Z-образного профиля
– полная длина Z-образного профиля
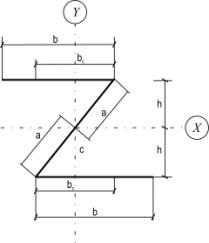
Рис. 1
Т.к.
данная форма сечения имеет центральную симметрию (т. С, рис.1), то центр тяжести сечения будет совпадать с центром
симметрии. Следовательно, все оси, проходящие через центр тяжести С являются центральными осями.
Определим диапазон изменения относительной длины свеса полки.
При 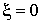 или b = 0 получаемый форму, изображенную
на рис.2, а при
или b = 0 получаемый форму, изображенную
на рис.2, а при 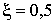 или
или 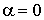 – на рис.3. Таким
образом, предварительно имеем диапазон
– на рис.3. Таким
образом, предварительно имеем диапазон
0< ξ< 0,5.
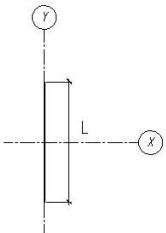
Рис.2
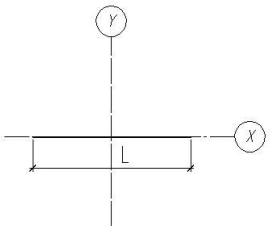
Рис.3
Учитывая
центральную симметрию сечения (т. С,
рис.1), центробежный момент инерции будем определять для верхней половины
сечения (рис.4)
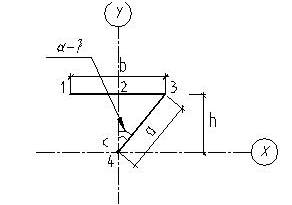
Рис.4
Предварительно
решим две задачи: найдем центробежный Jxy и осевой Jx моменты инерции полосы длиной l и толщиной δ = const,
0 ≤ s ≤
L (рис.5,6)
Задача №1 (рис.5):
Для элементарного участка ds:
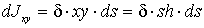 ,
, 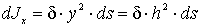 ;
;
Для всей полосы, длиной l:
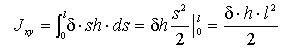 ,
, 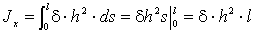 .
.
Задача №2 (рис.6):
Для элементарного участка ds:
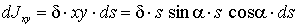 ,
, 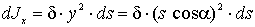 .
.
Для всей полосы, длиной l:
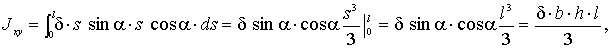
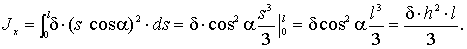
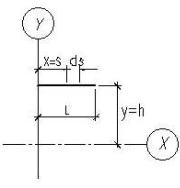
Рис.5
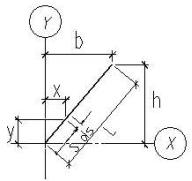
Рис.6
Тогда,
из рис.4, следует, что
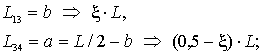
а так же
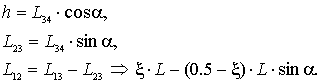
Из рис.4 следует, что центробежный момент инерции верхней
половины сечения равен нулю, если справедливо равенство
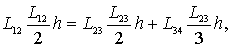
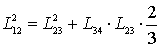 ,
,
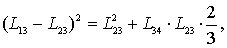
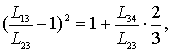
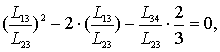
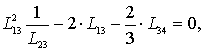
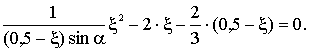
Или
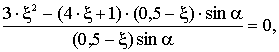 где
где 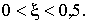
Тогда 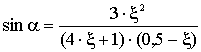 (1)
(1)
Следовательно, 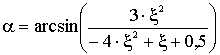 (2)
(2)
Установим
окончательные пределы изменения ξ:
т.к.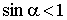 , то имеем неравенство
, то имеем неравенство 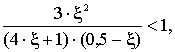
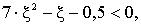
или 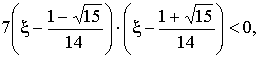
т.е. 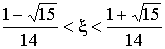 или
или 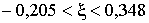 .
.
Из системы:
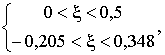
окончательно получаем диапазон
изменения относительной
длины свеса полки:
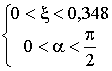 (3)
(3)
Литература:
1. Александров
А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. М:
Высш. шк., 1995. 560 с.
2. Власов
В.З. Избранные труды. В 3 т. / Т.2 Тонкостенные упругие стержни. Принципы
построения общей технической теории оболочек. М.: Изд-во АН СССР, 1963. 507с.
![]() . Вычисление
основных геометрических характеристик поперечного сечения в практических
расчетах можно существенно упростить, если ввести безразмерный коэффициент
ξ, характеризующий отношение длины свеса полки к полной длине профиля:
. Вычисление
основных геометрических характеристик поперечного сечения в практических
расчетах можно существенно упростить, если ввести безразмерный коэффициент
ξ, характеризующий отношение длины свеса полки к полной длине профиля:![]()
![]() – полная длина Z-образного профиля
– полная длина Z-образного профиля
![]() или b = 0 получаемый форму, изображенную
на рис.2, а при
или b = 0 получаемый форму, изображенную
на рис.2, а при ![]() или
или ![]() – на рис.3. Таким
образом, предварительно имеем диапазон
– на рис.3. Таким
образом, предварительно имеем диапазон




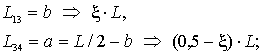
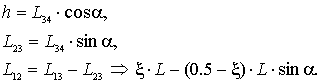
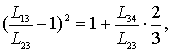
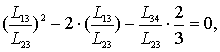
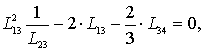
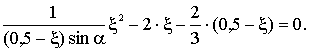
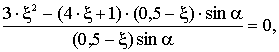 где
где