МОДЕЛЮВАННЯ ПРОЦЕСУ ЗАНУРЕННЯ ТІЛА В РОЗПЛАВ СТАЛІ

 ІЗ ЗАСТОСУВАННЯ ПРОГРАМНОГО КОМПЛЕКСУ FLOWVISION

В. А. Пасічник, І. С. Шумік

(Дніпропетровський національний університет ім. О. Гончара,

 e-mail: vmasterua@ua.fm)

 

Для виробництва легованої сталі і сплавів важливе значення має розроб­ка та удосконалення технологій введення розкислювачів у розплав сталі. На даний час найбільш поширеним є спосіб введення реагентів в розплав і перемішування розплаву металу, здійснюваний за допомогою примусового занурення завантаженого контейнера в розплав. При цьому для забезпечення однорідності розподілу реагентів в розплаві важливе значення має моделювання та розрахунок параметрів гідродина­мічних процесів занурення.

Метою даного дослідження є моделювання та аналіз параметрів гідродина­мічних процесів занурення тіл різної форми в розплав сталі. Покладаємо, що в циліндричну трубу заповнену розплавом сталі занурюється контейнер циліндричної форми різних розмірів. Розплав всередині циліндричної труби вважається нерухомим. Швидкість руху контейнера вважаємо достатньою для його занурення в розплав. При зануренні контей­нера в розплав необхідно визначити рух течії і вихорів які починають утворюватися. Таким чином, отримаємо наглядну картину вихрової течії для контейнера, що занурюється в циліндр. За наведеною моделлю проводимо розрахунки для циліндричного контейнера різних розмірів.

У даному випадку математична модель задачі описується рівняннями

 Навье-Стокса:

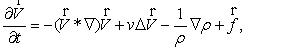                                       (1)

                                                                            (2)

де Ñ– оператор набла,  D – векторний оператор Лапласа, t – час, n – коефіцієнт кінематичної в’язкості, r – тиск, – векторне поле швидкостей,  – векторне поле масових сил. Невідомі r і  являються функціями часу t і координати  належать тривимірній області, в якій рухається рідина,

                                      (3)

Модель турбулентної нестисливої рідини базується на використані турбулентної в’язкості µt, визначення якої залежить від обраної моделі турбулентності. Для розрахунку будемо використовувати стандартну k-e модель, яка включає в себе наступні рівняння для k і e:

 

 

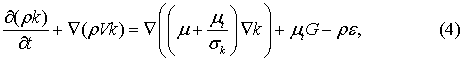
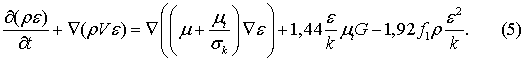
Крайова задача для рівнянь (1) – (5) визначається такими крайовими і початковими умовами.

На поверхні контейнера циліндричної форми задаємо такі умови.

1 – "вхід/вихід – нормальна швидкість":                      (6)

2 – "стінка": .                                                                         (7)

3 – "вільний вихід – нульовий тиск/вихід":

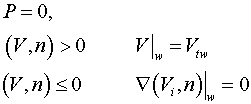                                                                   (8)

Для контейнера зануреного в рідину задаємо граничну умову "стінка". Схема розподілу граничних умов наведена на рис. 1.

Рисунок 1 – Схема розподілу крайових умов по поверхні контейнера

Для побудови розв’язку крайової задачі (1) – (8) застосовуємо програмний комплекс FlowVision, який дозволяє моделювати тривимірні течії рідини і газу для технічних і природних об’єктів, а також забезпечує візуалізацію цих течій методами комп’ютерної графіки.

Алгоритм побудови розв’язку:

1. Створюємо геометричну модель задачі: циліндрична труба не обмежена знизу (розміри: довжина – 4 м, діаметр – 1,38 м). Геометричні розміри тривимірної моделі тіла, яке занурюється в циліндр, визначаємо таким чином, щоб воно займало не більше 20 відсотків від діаметру труби, а маса була 25-30  кілограм.

2.  Експортуємо створену модель тривимірного тіла в  FlowVision.

3. Розрахункова модель задачі визначається рівняннями Навье-Стокса для течії нестисливої рідини.

4. Вводимо фізичні властивості розплаву сталі, яким заповнений циліндр:  щільність  - 7014 кг/м3 ;  молекулярна в’язкість -  0,0064 кг×м-1 ×с-1.

5. Вводимо крайові умови. Для циліндра ставимо для бокової поверхні крайову умову "стінка", на верхній поверхні - "вхід/вихід - нормальна швидкість " , на нижній поверхні - "вільний вихід - нульовий тиск/вихід ".

6. Створюємо розрахункову сітку. В даному випадку створюємо грубу сітку вздовж всього циліндра, і згущуємо (проводимо адаптацію розрахункової сітки за допомогою граничних умов) біля поверхні контейнера.

7. Проводимо розрахунок задачі, в процесі якого відслідковуємо за зміною картини течії. Розрахунок зупиняється, коли течію можна вважати усталеною.

Розрахункова сітка задається вздовж напрямку осей x, y, z, вказавши число розбиття. Таким чином ми задаємо сітку рівня 0, але в деяких випадках вона являється дуже грубою. Одним із способів підвищити точність, являється подрібнення сітки біля поверхні. Для цього в вікні властивостей граничних умов задається рівень адаптації. В такому випадку, всі комірки які знаходяться поблизу поверхні і містять цю граничну умову, будуть подрібнені до відповідного рівня.

FlowVision використовує прямокутну адаптивну локально подрібнену сітку (АЛПС) для розв’язання рівнянь математичної моделі. Можливість адаптації цієї сітки дозволяє враховувати достатньо малі особливості геометрії розрахункової області і високі градієнти величин, які розраховуються.

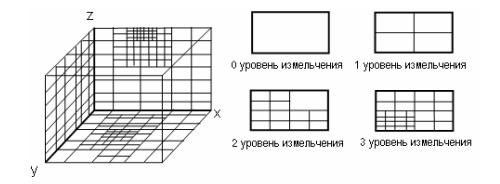
Рис. 2. Адаптивна сітка з локальним подрібненням

Результати  комп’ютерного моделювання показали, що від форми тіла та різної швидкості, з якою воно рухається, залежить динаміка руху розплаву сталі. Чим менша площа поперечного перерізу контейнера з розкислювачем і чим більша його швидкість, тим глибше воно зануриться в об’єм. Під час цього процесу найкраще можна оцінити гідродинамічні особливості взаємодії з розплавом. Найбільших значень швидкість руху рідини набуває навколо контейнера з розкислювачем, а ближче до стінок ковша швидкості починають зменшуватися. Поблизу поверхні контейнера утворюються вихори, напрями яких визначаються векторами швидкості його руху. Через певний час контейнер зупиняється та починає спливати, оскільки на нього діє не тільки сила тяжіння, а й за законом Архімеда виштовхувальна сила.

Результати проведеного дослідження дозволяють провести оптимізацію форми контейнера для введення реагентів в розплав сталі та забезпечення однорідності їх розподілу в металі при промисловому виробництві легованої сталі і високоякісних сплавів.