УДК 519.16, 621.39

К.т.н. Ткаченко В.Г.

Одесская национальная академия связи им. А.С. Попова, Украина

К.ф.н. Кокорев А.В.

Одесская национальная академия связи им. А.С. Попова, Украина

        

МЕТОД ПЕРЕБОРА ПРОСТЫХ ЦИКЛОВ И ОСТОВОВ ТЕЛЕКОММУНИКАЦИОННЫХ СЕТЕЙ

METHOD FOR TELECOMMUNICATION NETWORKS' SIMPLE

CYCLES AND SKELETONS ITERATION

 

В ряде случаев необходимо делать перебор остовов, базовых и простых циклов сети [1]. (Определения всех понятий из теории графов приведены в [1].) Прямой и обратный методы перебора остовов описаны в [2].

Однако эти методы не подходят для перебора базовых и простых циклов, хотя анализ простых циклов фрагментов сети важен для оптимизации сети.

Целью работы является разработка метода нахождения простых циклов и остовов телекоммуникационной сети за время сравнимое с нахождением исключительно остовов.

Монотонная булева функция (МБФ) – это булева функция, значение которой не уменьшается при увеличении любого из её аргументов. В [3] показано, что монотонные булевы функции можно представить в виде булевых выражений, где присутствуют только операции дизъюнкции и конъюнкции, но нет операции отрицания.

Двойственная МБФ – монотонная булева функция, в которой все операции конъюнкции заменены на операции дизъюнкции, а операции дизъюнкции, на операции конъюнкции.

Конъюнктивная нормальная форма (КНФ) — нормальная форма, в которой булева функция имеет вид конъюнкции дизъюнкций элементов.

Дизъюнктивная нормальная форма (ДНФ) — нормальная форма, в которой булева функция имеет вид дизъюнкции конъюнкций элементов.

Метод основан на получении простых циклов из базовых циклов. Затем  получается остовная МБФ как дизъюнктивное дополнение двойственной  МБФ простых циклов.

Перейдем к описанию предложенного метода. В качестве исходных данных используется представление сети в виде связанного графа, каждая из вершин которого имеет минимум два ребра.

Этапы алгоритма:

1.      Поиск произвольного остова сети.

2.      Поиск базовых циклов сети.

3.      Нахождение простых циклов сети.

4.      Нахождение коостовов сети путем раскрытия скобок в двойственной МБФ простых циклов.

5.      Нахождение остовов сети путем дизъюнктивного дополнения коостовной МБФ.

Рассмотрим этапы:

На первом этапе находим один, любой остов сети. Метод поиска остова не важен, так как не важны параметры ребер, но желательна максимальная разветвленность для простоты поиска простых циклов. К примеру, можно использовать алгоритм Дейкстры [1], считая вес каждого ребра за единицу. При этом желательно сохранить направление или путь прохождения для последующих этапов.

Для поиска базовых циклов достаточно по очереди перебирать ребра, не принадлежащие к остову, формируя базовые циклы. Найденные базовые циклы сохраняются для следующего этапа. Сохраненная информация маршрутов с предыдущего этапа сократит время определения маршрута цикла. К примеру, можно идти от вершин добавленного ребра к вершине отсчета алгоритма Дейкстры, вершина пересечения маршрутов от двух вершин нового ребра закрывает цикл.

Перебор всех комбинаций базовых циклов в виде МБФ сложением по модулю два позволяет получить все возможные простые циклы, но может сгенерировать несколько несвязных циклов представленных как один. Перебор осуществляется последовательным увеличением переменной-счетчика на 1, начиная с 1 до двоичного числа, состоящего из n единиц, где n – число ребер в сети. Возможно несколько методов фильтрации несвязанных циклов: по завершению формирования списка всех комбинаций проверить их на связность с использованием результатов работы алгоритма Дейкстры, проверить связность на основе метода представленного в статье [4], либо проверить на включения уже найденных циклов в текущий (минимизация). Представленные методы эффективны в разных условиях, их эффективность зависит от метода представления циклов и структуры сети.

Этап нахождения коостовов можно представить как преобразование КНФ в ДНФ. Однако вместо раскрытия скобок оптимальнее осуществить выборку всех подграфов с количеством ребер равным числу ребер, не вошедших в остов (числу ребер коостова), и затем проверку подграфов на принадлежность к ДНФ. При большом количестве элементов такой подход заменяет обычное раскрытие скобок и экономит ресурсы.

Полученные подграфы в составе ДНФ являются коостовами. Для получения МБФ остовов достаточно взять дизъюнктивное дополнение от ДНФ коостовов.

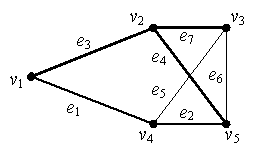
Разберем предложенный метод на примере сети  из 5 вершин и 7 ребер (рис. 1).

 

 

 

 

 

 


Рисунок 1 – Пример сети из 5 вершин и 7 ребер

 

В качестве произвольного остова выбираем подграф e1Úe3Úe4Úe7 (этот остов выделен на рис.1 жирной линией). Находим базовые циклы на его основе:

1) e1Úe2Úe3Úe4;

2) e1Úe3Úe5Úe7;

3) e4Úe6Úe7.

Простыми циклами являются все базовые, плюс комбинации полученные сложением по модулю два базовых циклов:

1) e1Úe2Úe3Úe4;

2) e1Úe3Úe5Úe7;

3) e4Úe6Úe7;

4) (e1Úe2Úe3Úe4) ⊕ (e1Úe3Úe5Úe7) = e2Úe4Úe5Úe7;

5) (e1Úe2Úe3Úe4) ⊕ (e4Úe6Úe7) = e1Úe2Úe3Úe6Úe7;

6) (e1Úe3Úe5Úe7) ⊕ (e4Úe6Úe7) = e1Úe3Úe4Úe5Úe6;

7) (e1Úe2Úe3Úe4) ⊕ (e1Úe3Úe5Úe7) ⊕ (e4Úe6Úe7) = e2Úe5Úe6.

Представляем все простые циклы в виде дизъюнкций, из входящих в эти циклы переменных. Обьединяя все эти дизъюнкции в КНФ, получаем двойственную МБФ простых циклов:

(e1Úe2Úe3Úe4)(e1Úe3Úe5Úe7)(e4Úe6Úe7)(e2Úe4Úe5Úe7)(e1Úe2Úe3Úe6Úe7)´

´ (e1Úe3Úe4Úe5Úe6)(e2Úe5Úe6).

МБФ простых циклов имеет следующий вид:

e1e2e3e4Úe1e3e5e7Úe4e6e7Úe2e4e5e7Úe1e2e3e6e7Úe1e3e4e5e6Úe2e5e6.

После преобразования КНФ в ДНФ раскрытием скобок в двойственной МБФ простых циклов и минимизации получаем коостовную МБФ из 24 коостовов:

e1e2e5Úe2e3e4Úe1e4e5Úe2e4e5Úe3e4e5Úe1e2e6Úe2e3e6Úe1e4e6Úe3e4e6Úe1e5e6Úe2e5e6Úe3e5e6Ú e4e5e6Úe1e2e7Úe2e3e7Úe2e4e7Úe1e5e7Úe2e5e7Úe3e5e7Úe4e5e7Úe1e6e7Úe2e6e7Úe3e6e7Úe4e6e7.

Получаем остовы взяв дизъюнктивное дополнение от МБФ коостовов:

e3e4e6e7Úe1e5e6e7Úe2e3e6e7Úe1e2e6e7Úe3e4e5e7Úe3e4e5e7Úe1e4e5e7Úe2e3e5e7Ú

e1e2e5e7Úe2e3e4e7Úe1e3e4e7Úe1e2e4e7Úe1e2e3e7Úe3e4e5e6Úe1e4e5e6Úe1e3e5e6Ú

e2e3e4e6Úe1e3e4e6Úe1e2e4e6Úe1e2e3e6Úe2e3e4e5Úe1e3e4e5Úe1e2e4e5Úe1e2e3e5.

В данном случае для перебора берутся сочетания по 3 из 7 – всего необходимо перебрать 35 значений. Всего в данном графе имеется 7 простых циклов. Из них один состоит из 3 ребер, 4 из 4 ребер и 2 из 5 ребер. При обычном раскрытии скобок  двойственной КНФ простых циклов получаем 34452 = 19200 конъюнкций без учета минимизации (при обычном раскрытии скобок количество получаемых элементов равно произведению количеств элементов в каждой из скобок). Преимущества предложенного метода перебора в сравнении с классическим раскрытием скобок в данном случае очевидно, и при росте количества ребер это преимущество быстро растет.

Литература

1.           Свами М. Графы, сети и алгоритмы / М. Свами, К. Тхуласираман. – М.: Мир, 1984. – 455 с.

2.           Ткаченко В.Г. Методы прямого и обратного перебора остовов графов телекоммуникационных сетей/ В.Г. Ткаченко, Д.Г. Ларин. //Труды одесского политехнического университета. – 2011. – № 2 (36) . – С. 210-216.

3.           Иваницкий А.М. Графы, матроиды, монотонные булевы функции и принцип взаимосоответсвия/ А.М. Иваницкий, В.Г. Ткаченко – Одесса, 2012. – 148 с.

4.           Ткаченко В.Г. Метод проверки связности и цикличности фрагмента сети на основе монотонных булевых функций/ В.Г. Ткаченко, А.О. Клещев //Наукові праці ОНАЗ ім. О.С. Попова. – 2011. – № 2. – С. 114-121. *