К.т.н. Евтушенко О.А.

Филиал «НИИ Аэронавигации» ФГУП ГосНИИ ГА, Москва, Россия,

Ермошенко Ю.М.

ООО «Аэроприбор», г. Москва, Россия

Модели динамики движения ВС и навигационных

измерений в аппаратуре потребителей СРНС

При анализе возможности повышения точности навигационных определений (НО) воздушных судов (ВС) с использованием спутниковой радионавигационной системы (СРНС) [1], необходимо задаться динамической моделью ВС. При этом, чтобы фильтрация навигационных параметров (нп), составляющих вектор состояния ВС

l = (х V_x y V_y z V_z Dt V_t)^T, включающий в себя координаты ВС х, y, z, составляющие его скорости V_x, V_y, V_z, сдвиг бортовой шкалы времени (БШВ) Dt и скорость его изменения V_t, обеспечивала наибольший выигрыш в точности, динамическая модель должна достаточно полно описывать движение объекта и быть удобной для реализации на ЭВМ [2] .

Этим условиям удовлетворяет марковская модель [3], в рамках которой динамика движения ВС в дискретном времени описывается разностным уравнением состояния

,

где F - диагональная блочная переходная матрица размером 4´4 с блоками вида

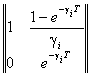, g_i = g_x, g_y, g_z ,

g_t - значения эффективной ширины спектра флуктуаций составляющих скорости ВС и скорости изменения сдвига БШВ,

T - шаг дискретизации,

n_i - описывающая динамические шумы последовательность гауссовых случайных векторов с диагональной блочной корреляционной матрицей Q размером 4´4 с блоками вида

,

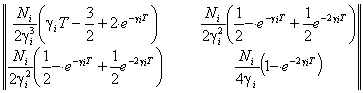где N_i - спектральные плотности флуктуаций составляющих скорости ВС и скорости изменения сдвига БШВ, связанные с соответствующими дисперсиями и значениями ширины спектра флуктуаций соотношением

N_i = 4 g_i.

При псевдодальномерном методе НО рабочее созвездие навигационных космических аппаратов (НКА) должно содержать не менее 4-х НКА. Вектор радионавигационных параметров (РНП) включает в себя псевдодальности r_i до НКА и псевдоскорости V_i ВС относительно них и записывается в виде:

r = (r₁ V₁ r₂ V₂ r₃ V₃ r₄ V₄)^Т.

При этом модель измерений имеет вид:

,

где H_i - значения матрицы направляющих косинусов в моменты измерений;

n_оi - описывающая шумы измерений последовательность гауссовых случайных векторов с диагональной ковариационной матрицей ошибок измерений РНП R размером 8´8, диагональные элементы которой - их дисперсии. При этом матрица направляющих косинусов имеет вид:

,

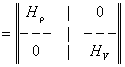где H_r и H_V - матрицы направляющих косинусов для r₁, r₂, r₃, r₄ и V₁, V₂, V₃, V₄, причем, H_V = H_r, а H_r - матрица размером 4 ´ 4, содержащая производные РНП r₁, r₂, r₃, r₄ по НП х, y, z, Dt.

Литература

1.Олянюк П.В. Спутниковые навигационные системы .АГА, СПб, 2008г, 98с

2. Строганова Е.П. Адекватность моделей и достоверность измерений РЭА // Т-Comm – Телекоммуникации и транспорт Спецвыпуск «Технологии информационного общества». Часть 3. Август. . 2009г с. 126 – 129.

3. Ярлыков М.С. Применение марковской теории нелинейной фильтрации в радиотехнике. - М.: Советское радио, 1980.