Математика/4.Прикладная математика

к.ф.-м.н. Джомартова Ш. А.

Казахский национальный университет имени аль-Фараби, Казахстан

Применение интервальной математики для оптимизации управления складским предприятием

В статье исследуется система управления запасами (многопродуктовая модель из n - продуктов), которая описывается линейными обыкновенными дифференциальными уравнениями

, (1)

где A(t) – nхn-матрица, элементы которой являются непрерывными функциями времени, B(t) – nхm-матрица, x(t) – n-мерный вектор состояния системы (количество товаров на складе), u(t) - m-мерный вектор управления (необходимое количество товаров).

Предполагается, что известен g(t) – n-мерный вектор - задающее воздействие (ожидаемый спрос на товары), которое удовлетворяет условию .

Исходя из практической постановки задачи на управления u(t) накладываются следующие ограничения

. (2)

Ограничение (2) имеет вполне естественный смысл: завозимый (приобретаемый на склад) товар не может иметь отрицательного значения и имеет реальное ограничение сверху (т.е. не может быть бесконечным).

На емкость склада накладываются условия (фазовые ограничения)

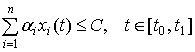. (3)

Любое складское помещение имеет естественное ограничение. В предлагаемой модели это ограничение характеризуется параметрами С и .

Кроме условия (3) на количество товара накладываются ограничения

. (4)

Считается известным состояние системы в начальный момент времени (начальное состояние - количество товара на складе в начальный момент времени)

. (5)

В соответствии с условиями (3) и (4) предполагается, что удовлетворяет условиям

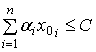и .

Желаемое состояние в конечный момент времени может быть описано как фиксированное

(6)

или подвижное (удовлетворяющее некоторым условиям – в случае, когда некоторые виды товаров являются взаимозаменяемыми и могут быть объединены в группы)

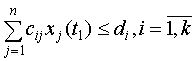. (7)

Для оценки качества работы системы (склада) может быть использован следующий критерии (функционал):

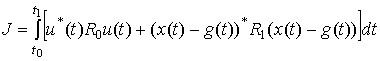, (8)

где - положительно-определенная mxm-матрица, - неотрицательно-определенная nxn-матрица.

Составим множество допустимых управлений

.

Это задача оптимального управления с ограничениями на управление (2), с фазовыми ограничениями (3)-(4), с закрепленными концами (5)-(6) или подвижными концами (5), (7). Момент времени считается заданным (фиксированным). На настоящее время решение подобных задач содержит ряд математических затруднений.

В последние годы получило развитие такое направление вычислительной математики как интервальная, оперирующая не с числами, а интервалами (которые позволяют учитывать погрешности задания исходных данных).

Далее применим интервальную математику для получения критерия удовлетворения спроса (за счет определения возможности приобретения товаров у поставщиков).

Пусть где - фундаментальная матрица решений системы однородных дифференциальных уравнений

.

Решение уравнения (1) можно представить в виде

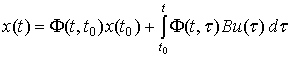. (9)

Введем обозначения

,

Тогда в случае ограничения (6) задача управляемости сводится к существованию решения системы интегральных уравнений

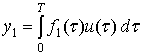, (10)

удовлетворяющего условию (2).

Заменяя управление интервалом и проводя интервальные вычисления по правилам, обозначим 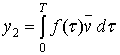, где - интервальный вектор.

Теорема. Для того чтобы система (1),(2),(6) была управляемой необходимо и достаточно, чтобы вектор принадлежал интервальному вектору .