К.э.н. Иванова И.А., Вачаева Л.П., Вачаева Т.П.

Мордовский государственный университет имени Н.П. Огарева, Россия

Анализ и прогнозирование ожидаемой продолжительности жизни как основного индикатора социального потенциала населения Республики Мордовия

Социальный потенциал представляет собой системную совокупность возможностей и мотиваций, способностей и качеств индивидов, социальных групп, общества, обеспечивающих их жизнедеятельность, социальную активность и его воспроизводство. В определённых условиях, при наличии необходимых ресурсов и потребностей его носителей социальный потенциал реализуется в труде. Ядром социального потенциала является человеческий потенциал, основными факторами развития которого являются: здоровье, образование, профессиональные знания, умения и навыки, благоприятные условия жизнедеятельности и труда. Поэтому не только в развивающейся, но и в кризисной экономике необходимым условием расширяющегося воспроизводства социального и человеческого потенциалов является сохранение благоприятных условий жизнедеятельности и труда, достойного труда, воспроизводства здоровья, возможностей переобучения и повышения профессиональной квалификации.

В целом социальный потенциал региона можно условно подразделить на два внутренних блока ресурсов: демографический потенциал и социальная инфраструктура региона.

Демографический потенциал характеризуется человеческими ресурсами и возможностью улучшения качества населения региона (определяется общей численностью населения, его половозрастным составом, динамикой роста (убыли) населения, миграционными процессами и т. п.), готовность к семейной жизни и воспитанию детей.

Демографический потенциал региона включают следующие составляющие:

1. Воспроизводство и физическое здоровье;

2. Интеллектуальные ресурсы (личности или совокупности лиц) ;

3. Культурно-нравственный потенциал ;

Второй блок в структуре социального потенциала региона включает социальную инфраструктуру, т. е. совокупность отраслей и видов деятельности, способствующих комплексному воспроизводству человека в процессе реализации его личных и общественных потребностей через предоставление различных услуг.

Социально-инфраструктурный потенциал характеризует резервы региона в сфере улучшения медицинского, бытового, культурного, транспортного и жилищно-коммунального обслуживания населения на основе расширения номенклатуры и повышения качества услуг, обеспечения их доступности для населения.

В качестве одного из основных индикаторов социального потенциала особое место занимает показатель ожидаемой продолжительности жизни при рождении. Это среднее количество лет, которое прожил бы новорожденный младенец при условии, что в каждом возрасте условия для сохранения его жизни оставались такими, какими они были для соответствующей возрастной группы в год его рождения.

Он отражает состояние окружающей среды в стране, здоровье ее населения, бытовые и прочие условия жизни, а также качество доступной медицинской помощи по состоянию на определенный год.

Как видно по данным ОПЖР за анализируемый период снизилась, и если в 1989 году она составляла 70,4 лет, то к 2009 году ОПЖР составила чуть больше 69 лет (рисунок 1).

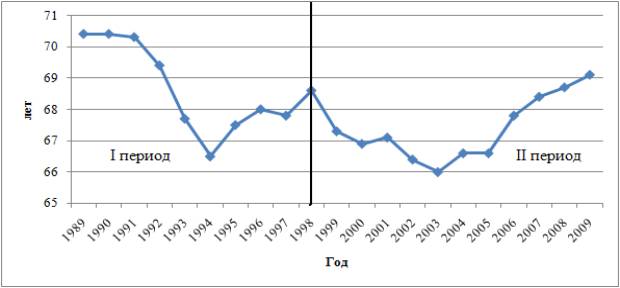
Рисунок 1 - Динамика ОПЖР населения Республики Мордовия

В динамике ОПЖР всего населения явно неоднородное изменение: за период 1990 – 1994 гг. снижение данного показателя составило 3,9 года; с 1994 по 1998 гг. происходило незначительное увеличение на 3,2 % (на 2,1 года); затем вплоть до 2003 года наблюдалось неуклонное снижение с 68,6 года до 66 лет. В настоящее время для данного показателя характерна тенденция к росту. Так в 2009 г. ОПЖР составила 69,1 лет, что на 4,7 % выше значения 2003 года.

Для показателя ОПЖР за 1989-2009 гг. характерны изменения, произошедшие под влиянием факторов, сложившихся в экономике России в эти годы. На графике видно, что исследуемый ряд предположительно можно разделить на 2 периода: 1989-1998 гг. и 1999-2009 гг., на каждом из которых явление развивается по параболической функции, т.е. в определенный момент времени t*=1998 г. происходит изменение характера динамики изучаемого показателя, и это непременно должно привести к изменению параметров уравнения тренда, которое может быть найдено с помощью аналитического выравнивания.

Для определения значимости влияния общих структурных изменений на характер тенденции используют тест Чоу, в котором проверяется гипотеза о структурной стабильности тенденции изучаемого временного ряда на основе сравнения расчетного и табличного значений F-критерия.

где – остаточная сумма квадратов по кусочной модели, которая определяется:

(3)

приращение остаточной суммы при переходе от единого уравнения тренда к кусочной модели:

(4)

С_ост - остаточная сумма квадратов уравнения тренда по всей совокупности, которая определяется как:

(2)

k₁ – число параметров в первом уравнении;

k₂ – число параметров во втором уравнении;

k₃ – число параметров в третьем уравнении;

n – число наблюдаемых единиц.

Табличное значение F-критерия определяется по таблице распределения Фишера для уровня значимости a и числа степеней свободы и

При сравнении возможны два варианта:

1) F_факт>F_табл. – гипотеза о структурной стабильности тенденции отклоняется, а влияние структурных изменений на динамику изучаемого показателя признают значимым. В этом случае моделирование тенденции временного ряда следует осуществлять с помощью кусочной модели;

2) F_факт<F_табл. – нет оснований отклонять гипотезу о структурной стабильности тенденции. Ее моделирование следует осуществлять с помощью единого для всей совокупности уравнения тренда.

Применим описанный метод к анализируемому ряду. Все расчеты производились в Excel и ППП «Statistica».

В результате получено, что с 95 % доверительной вероятностью гипотеза о структурной стабильности тенденции отклоняется, так как фактическое значение F-критерия больше табличного (F_факт = 4,118 >F_{табл. (0,05; 3; 15)} = 3,287). Влияние структурных изменений на динамику изучаемого показателя признают значимым, и для описания временного ряда необходимо использовать кусочную модель. В данном случае – полиномиальную модель 2-го порядка:

При использовании трендовых моделей в прогнозировании обычно предполагается, что основные факторы и тенденции прошлого периода сохраняются на период прогноза. Параметры моделей тренда, полученные методом наименьших квадратов, остаются неизменными в течение рассматриваемого периода, а как показывает практика – эти параметры меняются. Поэтому эффективными оказываются адаптивные методы, наиболее простым из многочисленного класса которых является метод экспоненциального сглаживания (метод Брауна). Его сущность заключается в том, что временной ряд сглаживается с помощью взвешенной скользящей средней. Причем при построении прогнозов с помощью данного метода одной из основных проблем является выбор оптимального параметра сглаживания a.

Результаты моделирования ОПЖР в РМ по методу Брауна представлены на рисунке 2, на основе которого был получен параметр сглаживания a=0,95.

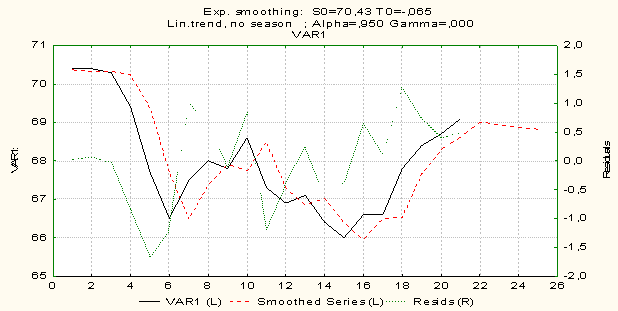
Рисунок 2 – Фактические данные, расчетные и прогнозные значения по модели Брауна для ОПЖР

Исследуемый временной ряд может быть также описан с помощью АРИСС-модели, которая относится к классу адаптивных моделей. Она объединяет модель авторегрессии и скользящего среднего. Такое объединение дает возможность более широкого применения и позволяет единым образом формировать прогноз на основе полученной модели.

Практическое использование АРИСС-моделей связывают с появлением методики их построения, разработанной Боксом и Дженкинсом. В этой методологии используется итеративный подход к определению допустимой модели среди общего класса АРИСС-моделей. Выбранная модель сопоставляется с исходными данными для проверки на сколько точно она описывает временной ряд данных. Модель считается приемлемой, если остатки в основном малы, случайно распределены и не содержат полезной информации.

С помощью ППП «Статистика» в результате перебора была подобрана модель порядка (0;2;2). В явном виде модель имеет вид:

Для того чтобы использовать полученные модели для прогноза дальнейшего развития исследуемого явления, была осуществлена проверка моделей на адекватность реальному процессу. В результате которой было получено, что все модели можно признать адекватными реальному процессу, так как случайная компонента E_t=– является а) случайной, б) независимой и в) нормально распределенной величиной. Следовательно, их можно использовать для построения прогноза.

Таким образом, для прогнозирования ожидаемой продолжительности жизни РМ были получены три модели: кусочно-полиномиальную модель 2-й степени, модель Брауна и АРИСС-модель. Выбор наилучшей модели осуществим на основе минимума средней ошибки аппроксимации (таблица 1):

Таблица 1 – Выбор модели для прогнозирования

Вид модели	Средняя ошибка аппроксимации, %
Кусочная модель	0,575
Модель Брауна	0,908
АРИСС-модель	0,861

Для прогнозирования была выбрана кусочно-полиномиальная модель 2-го порядка:

На основе данной модели был осуществлен точечный прогноз, а также построены верхняя и нижняя границы (таблица 2), найденные по следующей формуле:

Таблица 2 - Прогноз ОПЖР населения в РМ 2010-2012 гг., лет

Год	Прогнозные значения
	нижняя граница, 95%	точечный прогноз	верхняя граница, 95%
2010	69,773	70,439	71,106
2011	71,162	71,555	71,947
2012	72,557	72,808	73,060

Результаты построения прогноза на основе кусочно-полиномиальной модели представлены на рисунке 3:

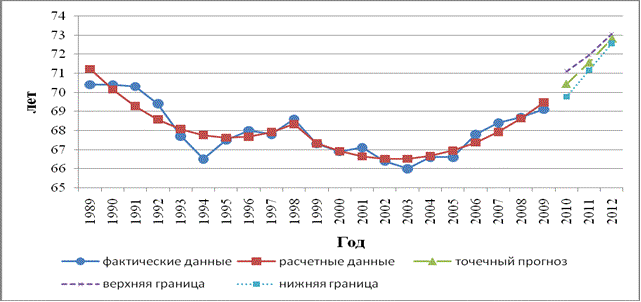
Рисунок 3 – Фактические и прогнозные значения ОПЖР в РМ, лет

На основе анализа графика можно сделать вывод, что в ближайшей перспективе в Республике Мордовия ожидается дальнейшая тенденция роста ожидаемой продолжительности жизни при рождении населения, значение которой в 2012 году будет варьироваться в пределах 72-73 лет.