К. ф.-м. н. Шумська А.А.

Національний технічний університет України

«Київський політехнічний інститут»

ПРИСКОРЕНЕ МОДЕЛЮВАННЯ НАДІЙНОСТІ ВІДНОВЛЮВАНОЇ СИСТЕМИ З ОБМЕЖЕНОЮ ВІДНОСНОЮ ПОХИБКОЮ ОЦІНКИ

Нестаціонарний коефіцієнт неготовності відновлюваної системи відноситься до найбільш важливих показників надійності. Вивчення реальних систем свідчить, що в багатьох випадках вони складаються з елементів істотно різної надійності. Це є суттєвою перешкодою ефективному використанню більшості існуючих методів. Саме на цьому випадку і сконцентрована увага у даній роботі. Метою дослідження є розробка методу прискореного моделювання, що є стійким відносно зміни надійності елементів.

Напрямок таких досліджень визначається ідеєю академіка НАН України І.М.Коваленка, що полягає у впорядкуванні траєкторій відмови системи за їх рангом (ранжування траєкторій) [1]. Це дозволяє подати нестаціонарний коефіцієнт неготовності у вигляді такого ряду, що кожний наступний його член має більш високий порядок малості порівняно з попереднім. Для обчислення членів ряду розроблено метод прискореного моделювання, що дає можливість отримувати оцінки з обмеженою відносною похибкою. Такий підхід разом з використанням методу розшарованої вибірки сприяв раціональній організації обчислювального експерименту. При цьому метод є дуже зручним для інженерної реалізації – при дослідженні конкретної системи досить провести лише розмітку елементів на більш і менш надійні. Оцінки лишаються незміщеними незалежно від зробленої розмітки. В той же час дисперсія оцінок істотно залежить від розмітки.

1. Принцип ранжування траєкторій

Розглянемо систему, що складається з елементів. Припустимо, що тривалості безвідмовної роботи елементів є незалежними випадковими величинами., які мають експоненціальний розподіл, – інтенсивності відмови елементів. Для відновлення елементів є ремонтних пристроїв. Якщо в момент відмови -го елемента є вільний ремонтний пристрій, то миттєво розпочинається відновлення цього елемента; час відновлення має функцію розподілу . Якщо ж всі ремонтні пристрої зайняті обслуговуванням, то елемент стає в чергу. Відновлення елементів проводиться в порядку виходу їх з ладу, тобто згідно з дисципліною обслуговування FCFS (First Come – First Served). Позначимо множину мінімальних перерізів відмов, де – кількість елементів у перерізі, а – номери цих елементів. Дана множина однозначно визначає всі стани несправності системи. В початковий момент усі елементи вважаються справними. Метою дослідження є розробка методу оцінки ймовірності несправності системи в фіксований момент часу .

При дослідженні реальних систем типовою є ситуація, коли елементи мають суттєво різну надійність, тобто інтенсивності мають різні порядки малості. На практиці досить легко провести порівняльний аналіз надійності елементів, поставивши у відповідність кожному з них деяке число , яке інтерпретується як порядок ненадійності -го елемента. Вважаємо, що приймають значення з множини натуральних чисел.

У подальшому важливу роль грає поняття траєкторії і, зокрема, траєкторії відмови. Траєкторією назвемо вектор номерів елементів, що відмовили в . При цьому цей вектор вважаємо впорядкованим, тобто (знак рівності з’являється з-за того, що один і той же елемент може відмовляти по декілька разів). Вектор не встановлює порядку, в якому відмовляють елементи; він лише вказує номери елементів, що відмовили в . Якщо в момент система виявиться несправною, то це буде траєкторія відмови. Рангом траєкторії назвемо . У випадку високонадійних елементів із зростанням рангу траєкторії ймовірність її виникнення зменшується. Позначимо множину траєкторій відмови з рангом . Тоді

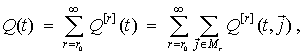(1)

де – мінімальний ранг, для якого множина є непустою, – ймовірність виникнення в траєкторії відмови , а – ймовірність несправності системи в момент завдяки траєкторіям рангу . Формула (1) лежить в основі запропонованого нижче методу обчислення ймовірності .

Навіть у випадку, коли для обчислення ймовірності існувала б явна аналітична формула, було б проблематично використати (1) для чисель-них розрахунків, оскільки множини містять величезну кількість траєкто-рій. Тому найбільш доцільним є використання методу Монте-Карло, зокрема прискореного моделювання. Але для цього спочатку треба розв’язати дві задачі. Першою з них є розробка алгоритму, що дозволив би перелічити всі траєкторії з множини , зокрема знайти їх кількість . Другою – розробка методу прискореного моделювання ймовірності для будь-якої фіксованої траєкторії .

2. Побудова множини траєкторій

Припустимо, що нам потрібно перелічити всі траєкторії з множини , поставивши у відповідність кожній траєкторії деяке натуральне число. Най-більш просто такий алгоритм формулюється за допомогою методу дерев.

Кожній вершині дерева поставимо у відповідність деяку траєкторію, причому ранг вершини – це ранг траєкторії. Вершину назвемо відміченою, якщо вона може породжувати інші вершини дерева. Таким чином, кожна вершина однозначно характеризується вектором , де – траєкторія, – її ранг, – індикатор того, що вершина є відміченою. Алгоритм побудови цього дерева формулюється таким чином.

1. Покладемо (лічильник кількості вершин рангу ). Кореню дерева відповідає вектор . Корінь може породити нових вершин , . Якщо , то , і ця вершина виключається із подальшого розгляду. Якщо , то і перевіряємо, чи є перерізом відмови системи. Якщо “ні”, то вершина виключається із подальшого розгляду. Якщо ж “так”, то траєкторія отримує номер і включається у множину . У випадку нова вершина може породжувати нові вершини дерева, тобто . Якщо розгорнуто всі вершини, то кореню дерева ставиться у відповідність вектор .

2. Розглянемо довільну відмічену вершину . Вона може породити нових вершин з . Якщо , то , і ця вершина виключається із подальшого розгляду. Якщо , то і перевіряємо, чи є перерізом відмови системи. Якщо “ні”, то вершина виключається із подальшого розгляду. Якщо ж “так”, то траєкторія отримує номер і включається у множину . У випадку нова вершина може породжувати нові вершини дерева, тобто . Після закінчення розгортання початкова вершина перестає бути відміченою, тобто їй ставиться у відповідність вектор . Алгоритм повторюється до тих пір, поки в дереві лишається хоча б одна відмічена вершина.

Очевидно, що даний алгоритм є скінченим, тобто він дозволяє за скінчену кількість кроків перелічити всі траєкторії множини .

3. Загальна схема методу обчислення ймовірності

Нехай – загальна кількість іспитів, яку ми плануємо використати для оцінки ймовірності , а – кількість іспитів для оцінки ймовірності , . Очевидно, що існує лише скінчена кількість додатних членів послідовності . Згідно з загальною схемою методу розшарованої вибірки оцінка для будується за формулою

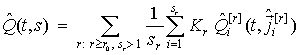, (2)

де – кількість траєкторій в множині , – траєкторія, що вибрана навмання (тобто рівноймовірно) з множини в -й реалізації, а – оцінка для , яка отримана в -й реалізації алгоритму при фіксованій траєкторії . Позначимо .

Загальна схема обчислення ймовірності методом розшарованої вибірки формулюється таким чином.

1. Для кожного за відносно невеликої кількості іспитів будуємо оцінку для . У випадку високонадійних елементів швидко прямує до нуля із зростанням . Тому, як правило, в сумі (2) треба враховувати лише декілька доданків з найменшими значеннями .

2. Кількість іспитів обчислюємо за формулою . Якщо , то покладемо . Якщо ж , то покладемо , де – ціла частина числа.

3. Результуючу оцінку будуємо за формулою (2), в якій оцінки знаходимо за допомогою окремого алгоритму.

4. Чисельний приклад

На чисельному прикладі дослідимо точність запропонованого методу. Для цього розглянемо систему, для якої ймовірність обчислюється за явною аналітичною формулою. Порівняємо оцінки , побудовані за допомогою запропонованого методу, з точними значеннями . Спочатку введемо позначення:

– кількість траєкторій відмови рангу ;

– оцінка для , що отримана методом розшарованої вибірки за формулою (2) із загальною кількістю іспитів ;

– вибіркова дисперсія, яка є сумою вибіркових дисперсій кожного з доданків формули (2);

– оцінка відносної похибки (вимірюється в процентах), що побудована за іспитами з достовірністю ;

– довірчий інтервал, побудований для за іспи-тами з достовірністю .

Постановка задачі. Нехай система складається з 9 елементів (). Інтенсивності відмови елементів задамо у вигляді . Припустимо, що час відновлення елементів також має експоненціальний розподіл, тобто . Існує достатня кількість ремонтних пристроїв, тобто відновлення починається одразу ж в момент відмови . Множина мінімальних перерізів відмови задається у вигляді (нагадаємо, що перша цифра в круглих дужках означає кількість елементів в перерізі). Таким чином, розглядається система, яка складається з трьох послідовно з’єднаних підсистем, що містять по 2, 3 та 4 паралельно з’єднаних елементів. Це той ідеальний випадок, коли поведінка системи може бути описана незалежними альтернуючими процесами відновлення, імовірнісні характеристики яких обчислюються за явними аналітичними формулами. Припустимо, що елементи в кожному перерізі мають ті ж самі характеристики надійності. Тоді

де

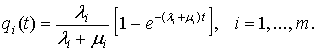
Задамо параметри, які визначають характеристики надійності елементів: (2, 2, 2, 2, 2, 1, 1, 1, 1), (0.5, 0.5, 0.4, 0.4, 0.4, 0.3, 0.3, 0.3, 0.3), (100, 100, 8, 8, 8, 15, 15, 15, 15). В цьому випадку мінімальним рангом буде . Обчислення показало, що кількість траєкторій відмови досить швидко зростає із збільшенням рангу: = 2, = 8, = 31, = 84, = 214, = 468, = 971, = 1848, = 3374, = 5824, = 9731, = 15628. Наведені дані свідчать, що коефіцієнт зростання () монотонно зменшується від 4 до 1.6.

В таблиці наведено результати моделювання, яке було проведено при фіксованому для різних значень . При кожному для отримання відповідних оцінок було зроблено по 100 000 іспитів.

Таблиця. Порівняння оцінок з точними значеннями

	0.001	0.01	0.1	1	10
	2.26	1.00	3.26	5.21	5.21
	2.25	0.99	3.30	5.16	5.33
	7.6	3.1	9.8	1.8	1.4
(%)	0.7	1.1	1.9	5.2	43.3
	2.23	0.99	3.24	4.89	3.02
	2.26	1.01	3.36	5.42	7.63

Коментуючи наведені в таблиці чисельні дані, перш за все зазначимо високу точність оцінок . Про це свідчить безпосереднє порівняння точних значень з оцінками , а також малі значення вибіркової дисперсії та відносної похибки . При всіх розглянутих значен-нях довірчий інтервал накриває точне значення . Спостерігається зростання відносної похибки із зростанням . Це пояснюється тим, що до моменту кожен з елементів може відмовити по декілька разів, і траєкторії мінімального рангу не мають істотного впливу на несправність системи в момент . Дисперсія оцінки, а як наслідок і відносна похибка, зростають за рахунок того, що потрібно враховувати траєкторії значно вищого рангу, кількість яких швидко зростає із збільшенням (див. наведені вище значення ). В той же час вже починаючи з , значення коефіцієнту неготовності мало чим відрізняються від його стаціонарного значення, тобто обчислення для можна не проводити.

Література:

1. Коваленко И.Н. Анализ редких событий при оценке эффективности и надежности систем. – М.: Сов. радио, 1980. – 209 с.

2. Kovalenko I.N., Kuznetsov N.Yu., Pegg Ph.A. Mathematical theory of reliability of time dependent systems with practical applications. – Chichester: Wiley, 1997. – 303 p.

3. Кузнецов Н.Ю., Шумская А.А. Моделирование монотонного отказа системы в случае различных порядков малости случайных величин, определяющих ее функционирование // Кибернетика и системный анализ. – 2005. – № 1. – С. 128-137.

4. Кузнецов Н.Ю. Условия ограниченности относительной погрешности при ускоренном моделировании надежности немарковских систем // Кибернетика и системный анализ. – 2006. – № 4. – С. 63-80.