Хандецький В.С., Мартинович Л.Я.

Дніпропетровський національний університет ім. О. Гончара

ДОСЛІДЖЕННЯ ВЗАЄМОДІЇ ПОЛЯ СТРУМОВОГО ВИТКА З ТОНКИМ СЛАБОПРОВІДНИМ КОМПОЗИТНИМ ШАРОМ

Багато задач прикладного характеру у різних галузях виробництва (машинобудування, приладобудування, виробництво напівпровідникових приладів, хімічних джерел струму, сонячних елементів тощо) пов’язано з вимірюванням електрофізичних параметрів тонких слабопровідних композитних шарів у вигляді плівок і різноманітних покрить безпосередньо в технологічному процесі, при переміщенні плівки ці стрічки з тонким слабо- провідним покриттям. В цих випадках принципово можуть застосовуватись лише безконтактні методи вимірювання.

Для визначення основних закономірностей взаємодії вісесиметричного електромагнітного поля витка, що живиться гармонійним струмом, з тонким слабопровідним шаром одержано наступний вираз (1), що визначає активний опір, внесений у виток вихоровими струмами, збудженими у шарі.

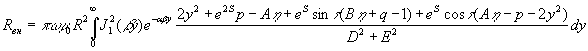, (1)

,

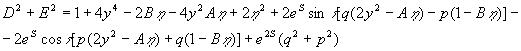де , , , , , ,

, , .

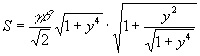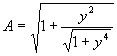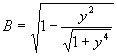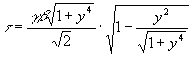Тут d- метрична товщина шару, ω- частота поля витка, σ – питома електрична провідність матеріалу шару, μ₀- магнітна постійна.

Представляє значний практичний інтерес залежність внесеного функціоналу F(ξ,β,α), який представляє інтеграл в (1) і визначає величину внесеного активного опору у токовий виток, від величини узагальненого зазору α=2h/R [1]. Вважаємо, що вісь витка є перпендикулярною до поверхні шару, при цьому h- величина метричного зазору між площиною витка з нехтувально малим перерізом і зовнішньою поверхнею шару, R – радіус витка. Дослідимо F(ξ,β,α) в діапазоні 0,001≤ ξ ≤ 0,1 , 0,01≤ β ≤ 0,1.

Значення F(α) при різних величинах ξ і β

Таблиця 1

α	F(α)
	ξ=0,001			ξ=0,01			ξ=0,1
	β=0,01	β=0,05	β=0,1	β=0,01	β=0,05	β=0,1	β=0,01	β=0,05	β=0,1
0,01	2,48	2,48	2,47	23,7	23,72	23,7	214	214	214
0,03	2,34	2,34	2,34	22,5	22,52	22,5	205	204,8	205
0,08	2,08	2,08	2,07	20,2	20,2	20,2	186	185,6	190
0,1	1,99	1,99	1,99	19,4	19,4	19,4	179	179,2	180
0,3	1,4	1,4	1,4	13,9	13,88	13,9	130	130	130
0,5	1,05	1,05	1,05	10,5	10,48	10,5	99	98,8	98,5
0,8	0,726	0,72	0,72	7,2	7,2	7,2	68	68,4	68
1	0,58	0,58	0,58	5,8	5,76	5,7	55	54,8	55

В стовпцях таблиці значення F(α) для β=0,01 помножені на 100, а для β=0,05 на 4. Як видно з даних таблиці, відповідні значення кожних трьох стовпців для кожного значення ξ практично повністю співпадають. Таким чином, вплив узагальненого параметра β в означених діапазонах β і ξ можна відобразити наступним чином:

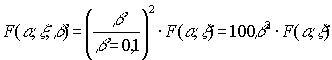. (2)

Розглянемо вплив узагальненої товщини шару ξ. Залежності F(α)

для β=0,1 і ξ=0,001, ξ=0,01 і ξ=0,1 показані на рис. 1.

Визначивши вплив на величину внесеного функціоналу F(ξ,β,α) узагальненого параметра β (2), тепер зафіксуємо його на максимальній межі діапазону β=0,1 і дослідимо залежності F від величини узагальненого зазору α для різних значень узагальненої товщини шару ξ.

Приймемо ξ=0,001. Для 0,01≤ α ≤ 1,0 одержимо:

100·F = 234,04·e^-1,4612α , R²=0,9898 . (8)

Для 0,01≤ α ≤ 0,8 - 100·F = 237,54·e^-1,5545α , R²=0,9902 . (9)

Для 0,01≤ α ≤ 0,5 - 100·F = 242,52·e^-1,7256α , R²=0,9923 . (10)

Для 0,01≤ α ≤ 0,3 - 100·F = 246,11·e^-1,9162α , R²=0,9924 . (11)

Для 0,01≤ α ≤ 0,1 - 100·F = 252,24·e^-2,413α , R²=0,9982 . (12)

α

F(α)

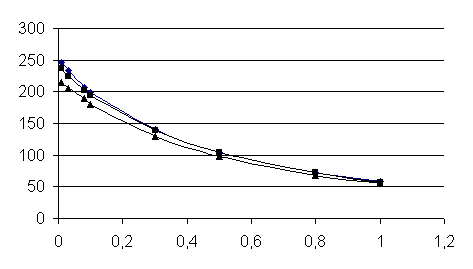
Рис. 1. Залежності F(α), що відображують вплив узагальненого зазору, для β=0,1 при ξ=0,001 (♦), ξ=0,01 (■), ξ=0,1 (▲). Значення F(α) для ξ=0,001 помножені на 100, а значення F(α) для ξ=0,01 помножені на 10.

Проаналізувавши залежності (8) – (12) можна побачити, що при звуженні діапазону α збільшується і абсолютна величина показника експоненти і коефіцієнт перед експонентою. Проте величина останнього змінюється дуже повільно. Позначивши цей коефіцієнт як С₀, одержимо, що його середнє значення дорівнює С_0,ср.=242,49, а максимальні відносні відхилення складають -3,4% і 4,0%. Позначимо абсолютну величину показника експоненти у виразах (8) – (12) буквою к , а верхню межу діапазону значень узагальненого зазору як α_u . Залежність величини к від α_u добре апроксимується як

к = 1,4756·α_u^-0,2152 , R²=0,9988 . (13)

Приймемо ξ=0,01. Середнє значення коефіцієнту С₀ дорівнює С_0,ср.=233,74, а максимальні відносні відхилення складають -2,8% і 3,3%. Залежність величини к від α_u має вигляд :

к = 1,4383·α_u^-0,1869 , R²=0,9987 . (14)

Приймемо ξ=0,1. Середнє значення коефіцієнту С₀ дорівнює С_0,ср.=213,6 , а максимальні відносні відхилення складають -2,3% і 1,8%. Залежність величини к від α_u має вигляд :

к = 1,4288·α_u^-0,1178 , R²=0,933 . (15)

Коефіцієнт вірогідності апроксимації R² [2] у цьому випадку менше, чим у попередніх для більш тонких шарів ξ=0,001 і ξ=0,01.

Звернемо увагу на величину коефіцієнта перед α_u у виразах (13), (14), (15). Позначимо його як d. Середнє значення d складає d_ср.=1,4476, а відносні відхилення дорівнюють 1,9% і -1,3%. Такими похибками у першому наближенні можна нехтувати, вважаючи d_ср= d в усьому діапазоні товщин шарів 0,001≤ ξ ≤ 0,1.

Визначимо вплив узагальненої товщини шару ξ на величину внесеного функціоналу F(ξ,β,α). На основі виразів (8)-(12) та рис.1 можна записати

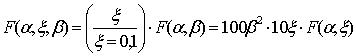. (16)

Розіб’ємо весь діапазон товщин 0,001≤ ξ ≤ 0,1 на три піддіапазони.

Для першого піддіапазону найбільш тонких шарів 0,001≤ ξ ≤ 0,01

F(α) = С₁exp(-dα·α_u^-λ1) , (17)

де С₁ =238,6 , λ₁=0,201 . Значення С₁ і λ₁ розраховані шляхом використання лінійної залежності між точками, що відповідають ξ=0,001 і ξ=0,01.

Для другого піддіапазону шарів середньої товщини 0,01< ξ ≤ 0,05 формула (17) не змінюється, проте коефіцієнти С₂ =230,35 , λ₂=0,1753 .

Для третього піддіапазону шарів найбільшої товщини 0,05< ξ ≤ 0,1 формула (31) також не змінюється, проте коефіцієнти С₃ =219,18 , λ₃=0,1369.

Величина α_u задає верхню межу для діапазону зазору між площиною витка зі струмом і поверхнею шару. Значення d для усіх трьох піддіапазонів приймається однаковим d =1,4476.

Узагальнюючи вирази (7), (30), (31) одержимо :

, (18)

де С_ξ і λ_ξ обираються відповідно до одного з трьох визначених вище піддіапазонів узагальненого зазору α.

Література

1. Соболев В.С., Шкарлет Ю.М. Накладные и экранные датчики.-Новосибирск : Наука, 1977.- 143 с.

2. Бабак В.П., Хандецький В.С., Шрюфер Е. Обробка сигналів.- Київ: Либідь, 1999.-495 с.