Мельник В.Н., Карачун В.В.

Национальный технический университет Украины «КПИ»

ВЛИЯНИЕ УГЛОВОГО ДВИЖЕНИЯ ИЗДЕЛИЯ НА ПОГРЕШНОСТЬ ИЗМЕРЕНИЙ

Нет сомнения, что наиболее типичным кинематическим возмущением здесь служит перемещение изделия в пространстве. Оставляя в стороне вопрос особенностей этого движения для аппаратов различного класса, остановимся на наиболее сложном из имеющихся – на угловом движении корпуса ракеты.

Свяжем с корпусом систему координат , причем ос направим вдоль ее продольной оси, а оси и расположим в плоскости шпангоута (рис. 1).

В качестве опорной системы координат выберем тройку осей, связанных с Землей: ось направим вертикально вниз, ось – расположим в горизонтальной плоскости, например, совместим с линией заданного курса, третью ось, ось , направим перпендикулярно первым двум.

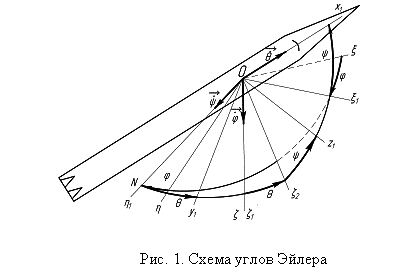
Пусть в момент старта ракета-носитель занимает произвольное положение. Проведем через ее центр масс плоскость, перпендикулярную продольной оси (плоскость шпангоута) до пересечения с горизонтальной плоскостью . По линии пересечения этих плоскостей, обозначим ее , направим ось и построим в горизонтальной плоскости ось , перпендикулярную .

В качестве углов Эйлера выберем угол поворота вокруг вертикали горизонтальной координатной плоскости до совпадения ее с осями . Этот угол назовем углом рыскания .

Угол поворота вокруг линии узлов координатной плоскости до

совмещения оси с продольной осью ракеты-носителя назовем углом тангажа и обозначим буквой . В этом случае ось займет положение в плоскости шпангоута.

Наконец, угол поворота плоскости вокруг продольной оси ракеты назовем углом крена и обозначим буквой .

Соответствующие принятой последовательности поворотов угловые скорости будут направлены по вертикали ,по линии узлов и вдоль оси РН (рис. 1).

В том случае, когда аппарат стартует с неподвижного основания, т.е. оси неподвижны, проекции угловой скорости на оси связанные с корпусом ракеты составляют:

(1)

Проекции угловой скорости на оси , связанные с поплавковым подвесом, имеют вид (рис. 2):

(2)

причем .

Если же старт осуществляется с орбитальной ступени, либо с площадки мобильного базирования, следует ее угловую скорость предварительно разложить по осям . В равной степени это относится к угловой скорости суточного вращения Земли.

В дальнейшем будем считать угол , а также производные по времени и малыми величинами. Угловую скорость представим в виде –

где – постоянная величина, измеряемая дифференцирующим гироскопом, например, при выполнении РН предусмотренного Полетным заданием маневрирования в вертикальной плоскости, т.е. по углу тангажа , а – малое возмущение этой угловой скорости. Такой режим имеет место, в частности, при движении аппарата по программной траектории в поисках цели.

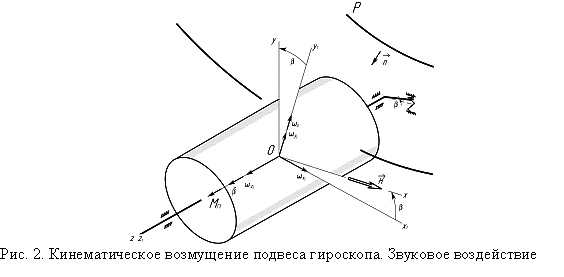
Из схемы, изображенной на рис. 2, следует, что составляющие и не оказывают влияния на погрешность измерений, т.к. совпадают с направлением вектора кинетического момента . В то же время, кинематические возмущения и приведут к появлению гироскопического момента (рис. 2):

(3)

Очевидно, что это погрешности измерений, обусловленные действием только одного внешнего фактора – углового движения корпуса ракеты.