Саржанов Т.С.
Казахский университет путей сообщения
МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ РАСЧЕТА УСТОЙЧИВОСТИ
БЕССТЫКОВОГО ПУТИ
Первые методы оценки
устойчивости пути с длинными рельсами появились еще в XIX веке. Они отражали лишь какой-то
определенный этап работы конструкции, который был исследован разработчиками
опытным путем. После появления бесстыкового пути со сварными стыками возникла
необходимость разработки теории его работы, которая бы реально отражала его
состояние в процессе эксплуатации.
Начало теоретических
исследований устойчивости бесстыкового пути относится к 1913 г. В последующие
годы были созданы разные варианты методов расчета величин продольных
критических сил в рельсах: энергетический, интегральных уравнений,
дифференциальных уравнений и др. Значительный вклад в решение этих вопросов
внесли российские ученые: В.Г. Альбрехт, М.С. Боченков,
Е.М. Бромберг, М.Ф. Вериго, Н.П. Виногоров, В.А.
Грищенко, Н.Б. Зверев, Э.П. Исаенко,
Н.И. Карпущенко, С.И. Клинов,
А.Я. Коган, А.А. Кривобородов, К.Н. Мищенко, С.И. Морозов, В.И. Новакович, С.П. Першин и другие, а так же зарубежные
ученые: О. Амман, М. Балух, К. Грюневальдт,
Д. Игнятич, Г. Майер, Нгуен
Ван Туен, И. Немешди-Немшек,
Э. Немежди и другие. В каждом из предложенных методов
сделаны, упрощающие расчетную схему допущения, приняты различные формы
деформаций рельсов в плане до выброса, имеются различия в исходных уравнениях
равновесия и в величинах задаваемых исходных данных.
Метод дифференциальных уравнений равновесия. Данный класс методов более точен, так
как уравнением упругой линии уже не задаются, а оно выводится в ходе решения и
полностью соответствует схеме нагружения [1,2].
Основное дифференциальное
уравнение изгиба имеет вид:
![]() (1)
(1)
Зная выражение для
изгибающего момента Мх
в любом сечении деформированного пути, получают дифференциальное уравнение в
развернутом виде. При этом по концам стержня приходится вводить опорные реакции
и опорные моменты.
Методом дифференциальных
уравнений пользовались многие ученые, как в России, так и за рубежом, начиная с
начала XX столетия.
Р. Леви составил систему
уравнений, симметричной половины волны, предполагая, что при волнообразном
искривлении реакция балласта в двух крайних четвертях волны уравновешиваются
реакциями двух средних четвертей.
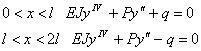 (2)
(2)
С.И. Морозов предложил
расчет устойчивости бесстыкового пути, использующий дифференциальное уравнение
изгиба балки:
![]() (3)
(3)
где q(y), m(y') - реактивная сила и момент; у, у0
- ординаты прогиба и начальных неровностей оси рельсошпальной решетки.
В. И. Новакович
предложил использовать элементы теории ползучести при расчетах бесстыкового
пути методом дифференциальных уравнений [3].
Д. Игнятич,
впервые ввел в дифференциальные уравнения устойчивости пути неравномерность
распределения сил сопротивления рельсошпальной решетки по длине пути, а так же
учел в расчетах начальные неровности пути и неравномерность нагрева плетей [4].
Наиболее полное решение
по определению устойчивости бесстыкового пути методом дифференциальных
уравнений дано в работах [1,2].
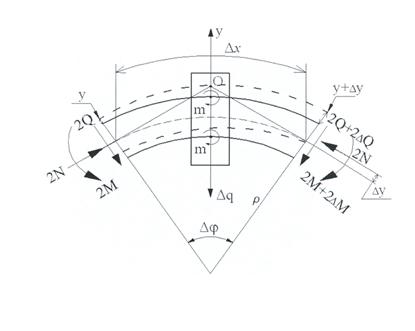
В основу положена
расчетная схема, изображенная на рис. 1.
Поставленная задача была
решена при следующих допущениях:
1) продольные силы в
обеих нитях одинаковы и постоянны N = const, величина продольной силы при этом равна
полусумме фактически действующих в обеих рельсовых нитях сил;
2) радиус кривизны обеих
нитей один и тот же ![]() , при этом кривизна
, при этом кривизна ![]() равна полусумме
кривизны наружной и внутренней нитей;
равна полусумме
кривизны наружной и внутренней нитей;
 3) при деформации пути шпалы
перемещаются параллельно сами себе.
3) при деформации пути шпалы
перемещаются параллельно сами себе.
Рисунок 1 - Расчетная
схема пути при использовании уравнения упругой оси
Как следует из второго
предположения, изгибающий момент и поперечная сила в обеих рельсовых нитях
одинакова.
Вырежем элемент пути![]() , размером, равным расстоянию между соседними шпалами и рассмотрим
его равновесие.
, размером, равным расстоянию между соседними шпалами и рассмотрим
его равновесие.
Составляя сумму моментов
относительно точки О, получим:
![]() (4)
(4)
где ![]() - приращение
изгибающего момента в рельсе на длине
- приращение
изгибающего момента в рельсе на длине ![]()
m - момент,
прикладываемый к рельсу со стороны скрепления
![]() - угол, стягивающий
дугу
- угол, стягивающий
дугу ![]()
![]() - приращение
поперечного перемещения рельса на дуге
- приращение
поперечного перемещения рельса на дуге ![]()
Деля равенство (5) на
величину 2![]() и учитывая соотношение:
и учитывая соотношение:
![]() (5)
(5)
получим равенство
![]() (6)
(6)
Учитывая приближенные
равенства отношений приращений, и отношений дифференциалов и вводя обозначение,
![]() (7)
(7)
которое выражает тот
факт, что момент m, приложенный от скрепления к рельсу,
зависит от угла скручивания рельса относительно шпалы, получим:
![]() (8)
(8)
Составим сумму проекций
сил на вертикальную ось:
![]() (9)
(9)
где ![]() - сила, передаваемая
на рельсы от шпалы
- сила, передаваемая
на рельсы от шпалы
![]() - приращение поперечной силы на дуге
- приращение поперечной силы на дуге ![]()
Деля равенство (9) на
величину 2![]() и учитывая соотношение:
и учитывая соотношение:
![]() (10)
(10)
получим
![]() (11)
(11)
Теперь, заменяя отношение
приращений отношением дифференциалов и вводя функцию:
![]() (12)
(12)
согласно которой сила,
приложенная к рельсу со стороны шпалы, зависит от перемещения, получим:
![]() (13)
(13)
Дифференцируя выражение (12)
и подставляя значение Q из формулы (11)
получим:
![]() (14)
(14)
Теперь воспользуемся
соотношением, определяющим момент в кривом стержне:
![]() (15)
(15)
Е
- модуль упругости рельсовой стали
![]() - момент инерции рельса относительно главной вертикальной оси
- момент инерции рельса относительно главной вертикальной оси
![]() - продольное перемещение сечения рельса
- продольное перемещение сечения рельса
Вторым членом в
соотношении (15) можно пренебречь в связи с его малостью. С учетом всего
вышесказанного получим следующее выражение:
![]() (16)
(16)
Кривизну рельса ![]() , представляем в виде суммы кривизны круговой кривой 1/R, (R-радиус круговой кривой) и кривизны
начальной неровности пути
, представляем в виде суммы кривизны круговой кривой 1/R, (R-радиус круговой кривой) и кривизны
начальной неровности пути ![]()
![]() (17)
(17)
После подстановки: ![]() получим основное
уравнение устойчивости бесстыкового пути:
получим основное
уравнение устойчивости бесстыкового пути:
![]() (18)
(18)
где R - радиус кривой
r, В, b- эмпирические коэффициенты к функциям сопротивлений
Это уравнение, без учета
начальных неровностей, решается следующей системой трансцендентных нелинейных
уравнений:
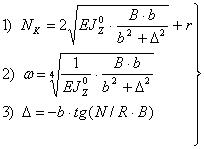 (19)
(19)
Данный метод позволяет
определить критическое состояние пути при заданных параметрах. Точность
решения при использовании этого метода зависит только от точности
аппроксимации коэффициентов к функциям различных сопротивлений.
В полном решении возможен
учет начальных напряженных и ненапряженных неровностей, неравномерности
распределения сопротивлений по длине пути (неравномерность затяжки клеммных
болтов и места с оголенными концами шпал), эксцентриситет приложения продольных
сил и.т.д.
Литература
1. Коган А. Я. Динамика
пути и его взаимодействие с подвижным составом. М.: Транспорт, 1997. - 326 с.
2. Коган А.Я., Грищенко
В.А. Нелинейная устойчивость бесстыкового пути в прямых участках при наихудшей
форме начальной ненапряженной неровности // Вестник ВНИИЖТ, 1992, №3. - С. 40-45.
3. Новакович
В.И. Бесстыковой железнодорожный путь с рельсовыми плетями
неограниченной длины. - Львов: Вища школа, 1984. -
98с.
4. Игнятич
Д.В. Определение критической силы, деформирующей бесстыковой
путь // Вестник ВНИЖТа, №8, 1965. - С. 7-11.