Ìàòåìàòèêà/4.Ïðèêëàäíàÿ ìàòåìàòèêà
ê.ô.-ì.í. Äæîìàðòîâà Ø. À.
Êàçàõñêèé íàöèîíàëüíûé óíèâåðñèòåò èìåíè
àëü-Ôàðàáè, Êàçàõñòàí
Interval
mathematics for practical calculations
In scientific researches, the engineering and mass
manufacture frequently should carry spend measurements of any sizes (length,
weight, force of a current etc.). At recurrence of measurements of the same
object which is carried out with the help of the same measuring device with
identical carefulness because of influence of the various factors, identical
data never turn out. The casual vibrations of separate parts of the device,
physiological changes of sense organs of the executor, various not taken into
account changes in environment (temperature, optical, electrical and magnetic
properties etc.) concern to number of such factors. Though the result of each
separate measurement at presence of casual dispersion cannot beforehand be
predicted, it corresponds «to a normal curve of distribution» (figure).
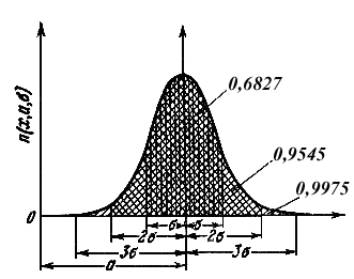
Figure Normal curve of distribution
From figure it is visible, that
basic weight of received results will be grouped about some central or average
meaning a, which the «true size» measurely of object answers unknown. The
deviations in this or that of the party will occur by that less often, than
more absolute size of such deviations, and are characterized by size ![]() - average quadratic deviation.
On a site from
- average quadratic deviation.
On a site from ![]() up to
up to ![]() There is on the average share
equal 0,6287 (of 68,27 %) of all weight of made repeated measurements. In
borders
There is on the average share
equal 0,6287 (of 68,27 %) of all weight of made repeated measurements. In
borders ![]() is placed on the average 0,9545
(95,45%) all measurements, and on a site
is placed on the average 0,9545
(95,45%) all measurements, and on a site ![]() - already 0,9973 (99,73%), so
for «three sigma» limits leaves only 0,0027 (0,27%) all number of measurements, i.e.
their insignificant share [1].
- already 0,9973 (99,73%), so
for «three sigma» limits leaves only 0,0027 (0,27%) all number of measurements, i.e.
their insignificant share [1].
«Classical» interval arithmetics assumes, that all
meanings of an interval are equiprobable [2,3]. Therefore all results received
with its help, cover every possible meanings and are «supersufficient».
In the given work new interval arithmetics which is
taking into account non-uniformity of distribution of meanings inside an
interval is offered.
Let's enter formal concept of an interval a in the
following kind:
![]() (1)
(1)
Where ![]() – middle of an
interval (or mathematical expectation),
– middle of an
interval (or mathematical expectation), ![]() – width of an
interval (or äèñïåðñèÿ). Let's
designate set of all such intervals as Iâåð(R).
– width of an
interval (or äèñïåðñèÿ). Let's
designate set of all such intervals as Iâåð(R).
Let a, b, c - intervals from Iâåð(R). Let's enter the
following interval arithmetic operations (in the assumption, that the intervals
are the independent normally distributed sizes):
1. Addition of two intervals a, bÎ Iâåð(R): a, bÎ Iâåð(R),
![]()
![]() (2)
(2)
2. Subtraction of two intervals a, bÎ Iâåð(R): ñ= a - b,
![]()
![]() (3)
(3)
3. Multiplication of two intervals a, bÎ Iâåð(R): ñ= a * b,
![]()
![]()
![]() (4)
(4)
4. Return interval àÎ Iâåð(R): ![]()
![]()
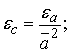 (5)
(5)
5. Division of two intervals a, bÎ Iâåð(R): ![]()
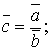
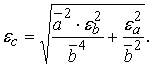 (6)
(6)
Let ![]() - independently distributed (independently
allocated) interval characterized by mathematical expectation (by middle of an
interval)
- independently distributed (independently
allocated) interval characterized by mathematical expectation (by middle of an
interval) ![]() and äèñïåðñèåé (in width of an interval)
and äèñïåðñèåé (in width of an interval) ![]() .
.
Function ![]() let is given interval meaning, which argument is in turn
interval. Meaning of this function will be an interval, which we shall
designate
let is given interval meaning, which argument is in turn
interval. Meaning of this function will be an interval, which we shall
designate ![]() , determined on the formula:
, determined on the formula:
![]() ,
, 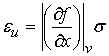 . (7)
. (7)
Let ![]() – independently
distributed intervals characterized by mathematical expectation (by middle of
an interval)
– independently
distributed intervals characterized by mathematical expectation (by middle of
an interval) ![]() and äèñïåðñèåé (in width of an interval)
and äèñïåðñèåé (in width of an interval) ![]() . Let's designate
. Let's designate ![]() .
.
Function ![]() let is given interval meaning, which arguments are in turn
intervals. Meaning of this function will be an interval, which we shall
designate
let is given interval meaning, which arguments are in turn
intervals. Meaning of this function will be an interval, which we shall
designate ![]() , determined on the formula:
, determined on the formula:
![]() ,
,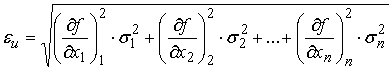 . (8)
. (8)
Let's compare entered interval arithmetics with «classical»
on examples.
1. Operation of addition (subtraction). Intervals ![]() and
and ![]() let are given.
let are given.
Then for new interval mathematics we shall receive the
following results:
![]() ,
,
![]() ,
,
Similarly for classical
interval mathematics:
![]() ,
,
![]() .
.
Thus, the centres of
both intervals coincide, however width of the entered interval (1.582) is less
than width of a «classical» interval (2.0).
2. Operation of multiplication. Intervals ![]() and
and ![]() let are given.
let are given.
Then for new interval
mathematics we shall receive the following results:
![]()
Similarly for classical
interval mathematics:
![]() ,
,
Thus, width of the
entered interval (1.803) is less than width of a «classical» interval (2.50)
and the centre of a «classical» interval is displaced on size 0.188.
3. Operation of
calculation of a return interval.
In «classical» calculation of a
return interval it is supposed, that ![]() . In the entered definition of a return interval it is supposed, that
. In the entered definition of a return interval it is supposed, that ![]() , if only
, if only ![]() .
.
Example. Intervals ![]() and
and ![]() let are given.
let are given.
Then for new interval
mathematics we shall receive the following results:
![]() ,
, ![]() .
.
Similarly for classical
interval mathematics:
![]() ,
, ![]() , does not exist.
, does not exist.
Thus, the centre of a «classical» interval ![]() is displaced on size 0.08.
is displaced on size 0.08.
4. Operation division of
two intervals.
For example, for intervals ![]() and
and  we shall receive
we shall receive
![]() ,
,  ,
, 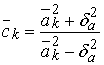 ,
, 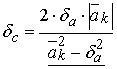 .
.
The centre of the entered interval is equal 1. The
centre of a «classical» interval is displaced rather 1, though contains 1.
At ![]() ànd
ànd ![]() we shall receive
we shall receive
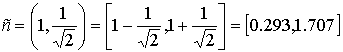 ,
, ![]() .
.
Thus, width of the entered interval is equal 1.414 and
less than width of a «classical» interval, which is equal 2.666. Besides the
centre of a «classical» interval is displaced from 1 on size 0.666.
Example. Intervals ![]() and
and ![]() let are given.
let are given.
Then for new interval
mathematics we shall receive the following results:
![]()
Similarly for classical
interval mathematics:
![]() .
.
Thus, width of the entered interval (0.113) is less
than width of a «classical» interval (0.162) and the centre of a «classical»
interval is displaced on size 0.030.
Example. Intervals ![]() and
and ![]() let are given.
let are given.
Then for new interval mathematics we
shall receive the following results: ![]() , is similar for classical interval mathematics:
, is similar for classical interval mathematics: ![]() , does not exist.
, does not exist.
5. Operation of
calculation of interval functions
Let ![]() – interval meaning function of interval
argument.
– interval meaning function of interval
argument.
Then for ![]() we shall
receive: for new interval mathematics
we shall
receive: for new interval mathematics
![]()
 (9)
(9)
For classical interval
mathematics
![]() where
where ![]() (10)
(10)
As it is visible from the above mentioned formulas for
differentially of functions of
calculation of meanings of function on new interval mathematics (9) more
structurally in view of ending
of carried out arithmetic operations. At the same time calculations under the
formulas (10) require the decision two optimization of tasks, for the decision
generally is necessary for each of which realization of iterative calculations.
Thus there are problems of convergence of iterative process and choice of an
index point.
References
1. Ñìèðíîâ Í.Â., Äóíèí-Áàðêîâñêèé
È.Â. Êóðñ òåîðèè âåðîÿòíîñòåé è ìàòåìàòè÷åñêîé ñòàòèñòèêè äëÿ òåõíè÷åñêèõ ïðèëîæåíèé.
– Ì.: Íàóêà, 1969.– 512 ñ.
2. Alefeld, G. and Herzberger, J.: Introduction
to Interval Computations, Academic Press, New York, 1983.
3.
Øîêèí
Þ.È. Èíòåðâàëüíûé àíàëèç. – Íîâîñèáèðñê: Íàóêà, 1986. – 224 ñ.