Горбатенко Я. В.

Навчально-науковий комплекс “Інститут прикладного системного аналізу” при НТУУ “КПІ”, Київ, Україна

Існування та єдиність слабких розв’язків півлінійних диференціальних рівнянь другого порядку в банаховому просторі

Нехай – банахів простір, – операторна косинус-функція із генератором . Оператор також є генератором синус-функції та аналітичної півгрупи . Нехай спочатку . Для покладемо

.

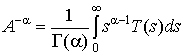Оператор обмежений в та має обернений. Покладемо . замкнений та щільно визначений [1].

Якщо , існує , для якого . Нехай , , ; для покладемо . Простір не залежить від вибору ; повний відносно норми та при різних відповідні норми еквівалентні [1].

Нехай також виконується наступне припущення: , а – сильно неперервна функція аргументу на . Це припущення виконується для будь-яких генераторів косинус-функцій в просторах [2].

Для функцій, що приймають значення в банаховому просторі , розглянемо наступне рівняння

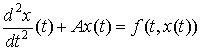, (1)

де функція відображає деяку відкриту множину в , , та поставимо для нього задачу Коші

(2)

Класичним розв’язком задачі (1)-(2) на називається функція , двічі неперервно диференційовна, для усіх , що задовольняє рівностям (1)-(2). Слабким розв’язком (mild solution) задачі (1)-(2) на називається неперервна функція , що задовольняє на рівняння

Класичний розв’язок задачі (1)-(2) є також слабким розв’язком, але не навпаки.

Теорема 1. Нехай задана відкрита множина та неперервна функція , що задовольняє умову Ліпшица: для будь-якої точки існує таке , що в деякому околі точки виконується нерівність

.

Тоді для кожної пари із та існує таке, що існує єдиний слабкий розв’язок задачі (1)-(2) на із , .

Теорема 2. Нехай неперервна функція в рівнянні (1) задовольняє глобальній умові Ліпшица: існує таке, що при та виконується нерівність

.

Тоді , існує єдиний слабкий розв’язок задачі (1)-(2) на із , .

Приклад. Розглянемо рівняння

.

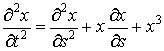В функціональній постановці йому відповідає рівняння

,

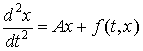де – функція зі значеннями в , , . Поставимо для нього задачу Коші:

.

Ця задача має єдиний локальний розв’язок.

Література:

1. D. Henry, Geometric Theory of Semilinear Parabolic Equations, Springer-Verlag, Berlin, Heidelberg, New York, 1981.

2. H. O. Fattorini, Second Order Linear Differential Equations in Banach Spaces, Elsevier Science Publishers B. V., Amsterdam, 1985.