М.П. Ленюк, Т.М. Олійник
МОДЕЛЮВАННЯ
ДИФУЗІЙНИХ ПРОЦЕСІВ МЕТОДОМ ГІБРИДНОГО ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА БЕССЕЛЯ –
ЛЕЖАНДРА – ФУР'Є НА ПОЛЯРНІЙ ОСІ З М’ЯКИМИ МЕЖАМИ СПРЯЖЕННЯ
Процеси
дифузії, які постійно відбуваються в навколишньому середовищі, привертають до
себе увагу вчених на протязі всієї історії людства. Найпростішою математичною
моделлю такого процесу є диференціальне рівняння дифузії (теплопровідності)
параболічного типу [1].
![]() (1)
(1)
з відповідними початковою умовою та крайовими
умовами.
Потреби
практики приводили до різноманітного узагальнення рівняння (1). Та в усіх
випадках дифузійні процеси вивчалися в припущенні, що межа середовища жорстка
по відношенню до відбиття хвиль. Різко змінюється картина дифузії, якщо межа
середовища є м’якою по відношенню до відбиття хвиль (в крайових операторах та
операторах спряження наявність похідної стосовно часової змінної).
Для
вивчення стану композитних матеріалів був поширеним в другій половині XX
століття метод кусково-сталих фізико-технічних характеристик [2]. Це приводило
до розв’язання диференціальних рівнянь із сингулярними коефіцієнтами типу
дельта-функції та похідних від неї. Та одержати аналітичне зображення точного
розв’язку задачі цим методом неможливо. Тому ми пропонуємо здійснювати
моделювання дифузійних процесів методом гібридних диференціальних операторів.
Побудуємо
обмежений в області ![]()
![]() розв’язок сепаратної системи
диференціальних рівнянь дифузії параболічного типу [1]
розв’язок сепаратної системи
диференціальних рівнянь дифузії параболічного типу [1]
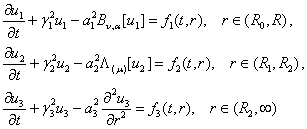 (2)
(2)
за початковими умовами
![]() (3)
(3)
та умовами спряження
![]() (4)
(4)
У
рівностях (2) беруть участь диференціальні оператори Бесселя ![]() [3], Лежандра
[3], Лежандра ![]()
![]() [4], та Фур’є
[4], та Фур’є ![]() [5],
[5], ![]()
![]() .
.
У
рівності (4) беруть участь узагальнені диференціальні оператори спряження
![]()
Будемо
припускати, що виконані умови на коефіцієнти:
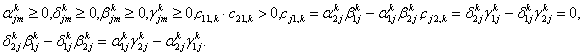
Припустимо,
що функції ![]() ,
, ![]() та
та ![]() є оригіналами за
Лапласом стосовно
є оригіналами за
Лапласом стосовно ![]() [6]. У зображенні за
Лапласом параболічній задачі (2) – (4) відповідає крайова задача: побудувати на
множині
[6]. У зображенні за
Лапласом параболічній задачі (2) – (4) відповідає крайова задача: побудувати на
множині ![]() обмежений розв’язок сепаратної
системи диференціальних рівнянь Бесселя, Лежандра та Фур’є для модифікованих
функцій
обмежений розв’язок сепаратної
системи диференціальних рівнянь Бесселя, Лежандра та Фур’є для модифікованих
функцій
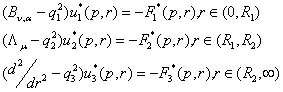 (5)
(5)
за умовами спряження
![]() (6)
(6)
У
рівностях (5), (6) прийняті позначення:
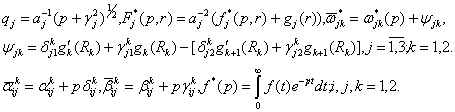
Фундаментальну
систему розв’язків для диференціального рівняння Бесселя ![]() утворюють функції
утворюють функції ![]() та
та ![]() [3]; фундаментальну систему розв’язків для диференціального
рівняння Лежандра
[3]; фундаментальну систему розв’язків для диференціального
рівняння Лежандра ![]() утворюють узагальнені приєднані
функції Лежандра
утворюють узагальнені приєднані
функції Лежандра ![]() та
та ![]() [4]; фундаментальну
систему розв’язків для диференціального рівняння Фур’є
[4]; фундаментальну
систему розв’язків для диференціального рівняння Фур’є ![]() утворюють функції
утворюють функції ![]() та
та ![]() [5].
[5].
Наявність фундаментальної системи розв’язків
дозволяє побудувати розв’язок крайової задачі (6), (7) методом функцій Коші
[5,7]:
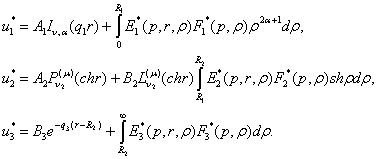 (7)
(7)
У рівностях (7) ![]() функції Коші [5,7]:
функції Коші [5,7]:
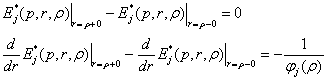 (8)
(8)
Тут ![]() .
.
Припустимо,
що функція Коші
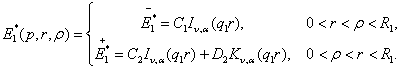
Властивості
(8) дають алгебраїчну систему:
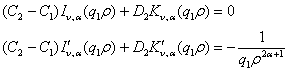
Звідси
отримуємо співвідношення:
![]() (9)
(9)
Доповнимо
рівності (9) алгебраїчним рівнянням:
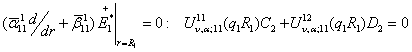 (10)
(10)
Із
алгебраїчної системи (9), (10) знаходимо, що
![]()
Цим
функція Коші ![]() визначена й внаслідок симетрії
відносно діагоналі
визначена й внаслідок симетрії
відносно діагоналі ![]() має структуру:
має структуру:
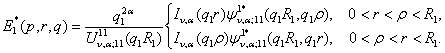 (11)
(11)
У
рівності (11) беруть участь функції:
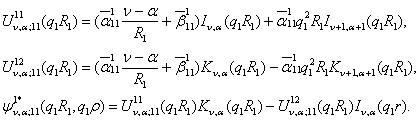
Припустимо,
що функція Коші
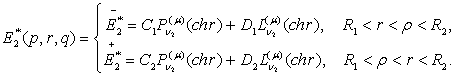
Властивості
(9) функції Коші дають алгебраїчну систему з двох рівнянь:
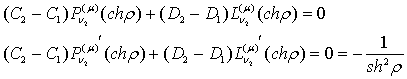
Звідси
отримаємо співвідношення:
![]() (12)
(12)
Доповнимо
рівності (12) алгебраїчними рівняннями:
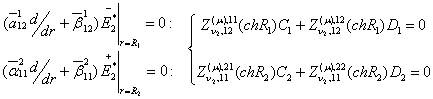 (13)
(13)
Із
алгебраїчної системи (12), (13) знаходимо, що
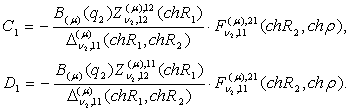 (14)
(14)
Цим
функція Коші ![]() визначена й внаслідок симетрії відносно
діагоналі
визначена й внаслідок симетрії відносно
діагоналі ![]() має структуру:
має структуру:
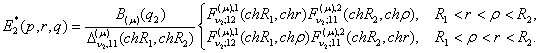 (15)
(15)
У
рівностях (13)-(15) беруть участь функції:
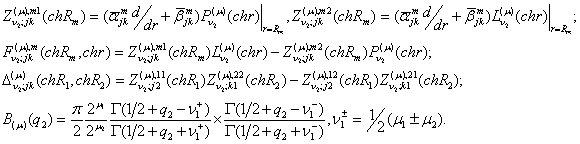
Припустимо,
що функція Коші
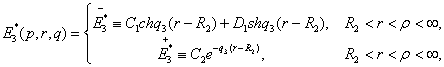
Властивості
(9) функції Коші дають алгебраїчну систему
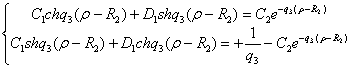
Звідси
маємо співвідношення:
![]() (16)
(16)
Доповнимо
рівності (16) алгебраїчним рівнянням:
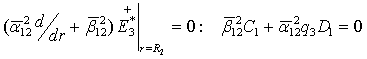 (17)
(17)
Із
алгебраїчної системи (16), (17) знаходимо, що
![]()
Цим
функція Коші ![]() визначена й внаслідок симетрії
відносно діагоналі
визначена й внаслідок симетрії
відносно діагоналі ![]() має структуру:
має структуру:
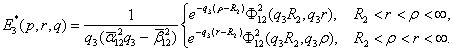 (18)
(18)
Повернемось
до формул (7). Умови спряження (6) для визначення невідомих ![]() дають алгебраїчну
систему з чотирьох рівнянь:
дають алгебраїчну
систему з чотирьох рівнянь:
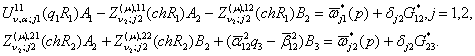 (19)
(19)
У системі (19) беруть участь функції

та символ Кронекера ![]() .
.
Введемо
до розгляду функції:
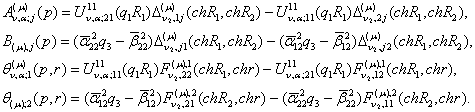
Припустимо,
що виконана умова однозначної розв’язаності даної параболічної задачі: для ![]() із
із ![]() , де
, де ![]() абсциса збіжності
інтеграла Лапласа, та
абсциса збіжності
інтеграла Лапласа, та ![]() визначник
алгебраїчної системи (19)
визначник
алгебраїчної системи (19)
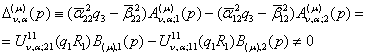 (20)
(20)
Визначимо
головні розв’язки крайової задачі (5), (6):
1)
породжені неоднорідністю умов спряження функції Гріна
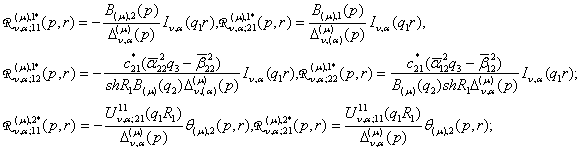
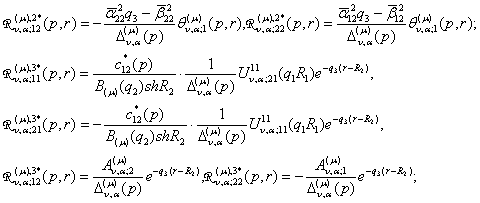 (21)
(21)
2)
породжені неоднорідністю системи (6) функції впливу
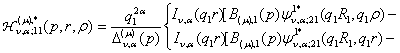
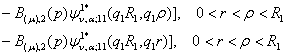
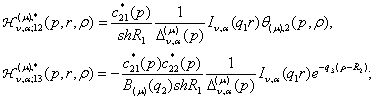
![]() (22)
(22)
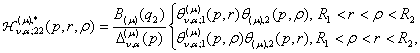
![]()

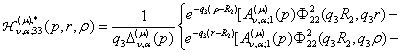
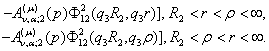
У результаті однозначної розв’язності алгебраїчної системи
(20) та підстановки отриманих значень ![]() у рівності (8) маємо
єдиний розв’язок крайової задачі (6), (7):
у рівності (8) маємо
єдиний розв’язок крайової задачі (6), (7):
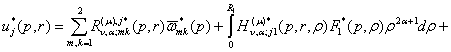
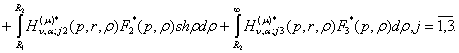 (23)
(23)
Повертаючись
в (23) до оригіналу, одержуємо єдиний розв’язок параболічної задачі (2) – (4):
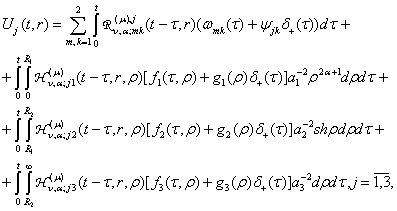 (24)
(24)
![]() дельта-функція, зосереджена в точці
дельта-функція, зосереджена в точці
![]() [7].
[7].
У
рівностях (24) за означенням [6]
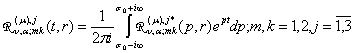 (25)
(25)
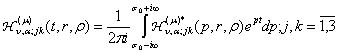 (26)
(26)
Особливими точками функцій Гріна ![]() та функцій впливу
та функцій впливу ![]() є точки галуження
є точки галуження ![]() та
та ![]() . Оскільки
. Оскільки ![]() , то всі особливі точки знаходяться на лівій дійсній піввісі
комплексної
, то всі особливі точки знаходяться на лівій дійсній піввісі
комплексної ![]() площини (
площини (![]() ). У такому випадку можна «сісти на уявну вісь» й отримати
для головних розв’язків даної параболічної задачі розрахункові формули:
). У такому випадку можна «сісти на уявну вісь» й отримати
для головних розв’язків даної параболічної задачі розрахункові формули:
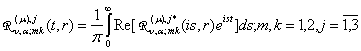 (27)
(27)
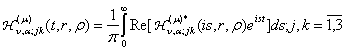 (28)
(28)
У рівностях (27), (28) ![]() означає дійсну
частину виразу
означає дійсну
частину виразу ![]() .
.
Зауваження 1. Можна вважати, що ![]() . В протилежному випадку переходимо до нових початкових умов
. В протилежному випадку переходимо до нових початкових умов
![]()
й знаходимо числа ![]() та
та ![]() із алгебраїчної
системи
із алгебраїчної
системи
![]() (29)
(29)
Тут ![]() .
.
Зауваження 2. Вибором параметрів, які беруть участь у
формулюванні даної задачі дифузії, можна виділити із загальних структур
безпосередньо будь-який частковий (практично важливий) випадок (в рамках даної
моделі).
Зауваження 3. При ![]() одержуємо випадок,
коли межі спряження є жорсткими по відношенню до відбиття хвиль.
одержуємо випадок,
коли межі спряження є жорсткими по відношенню до відбиття хвиль.
Література:
1.
Тихонов А.Н., Самарский
А.А. Уравнения математической физики. – М.: Наука, 1972. – 735с.
2.
Коляно Ю.М. Методы
теплопроводности и термоупругости неоднородного тела. – К.: Наук. думка, 1992.
– 280с.
3.
Ленюк М.П. Исследование
основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев,
1983. – 62с. – (Препринт / АНУССР. Ин-т Математики; 83-3).
4.
Конет І.М., Ленюк М.П. Інтегральні
перетворення типу Мелера – Фока. – Чернівці: Прут, 2002. – 248с.
5.
Степанов В.В. Курс
дифференциальных уравнений. – М.: Физматгиз, 1959. – 468с.
6.
Лаврентьев М.А., Шабат
Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1987. – 688с.
7.
Шилов Г.Е.
Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328с.