Экономические науки/8.Математические методы в экономике.

Шульгина-Таращук А. С.

Карагандинский Государственный Университет имени Е. А. Букетова,

Республика Казахстан

Простейшая модель и формулы Уилсона

Рассмотрим простейшую модель, предполагающую отсутствие неопределенностей, которая лежит в основе других, существенно более сложных и развитых моделей управления запасами [1].

Продукция поступает на склад, хранится там и уходит со склада в соответствии со спросом. В простейшей модели все полностью прогнозируемо, интенсивность спроса известна и постоянна. Обозначим ее через , то есть в единицу времени со склада перемещается единиц продукции.

На складе запас пополняется периодически и одинаковыми поставками (партиями). Пусть Т – период времени между поставками (длина цикла), Q – размер партии.

Дефицит в простейшей модели – явление недопустимое. Слишком ранний приход поставки, когда запас еще имеется, не выгоден, поскольку необходимо хранить лишний запас (и, следовательно, раньше времени оплачивать поставку).

Так как неопределенность отсутствует, то все можно спрогнозировать и рассчитать. Очередная партия должна приходить в тот момент, когда запас на складе опускается в точности до 0. В момент поставки размер запаса поднимается вверх на величину поставки Q, а затем расходуется с постоянной интенсивностью .

Размер партии и длина цикла связаны соотношением:

Q=Т.

Пополнять запас можно большими партиями через длинные промежутки времени, а можно – малыми партиями, через короткие промежутки. Задача состоит в том, чтобы определить оптимальный размер партии и оптимальную длину цикла.

Рассмотрим средние затраты в единицу времени. Так как ситуация повторяется циклически, то оптимизационные расчеты достаточно провести для одного цикла. На промежутке времени Т постоянная составляющая затрат равна х (одна поставка), переменная составляющая затрат равна 0,5QТу (площадь треугольника, умноженная на коэффициент у). Общие затраты на промежутке Т равны сумме этих двух составляющих, а средние затраты L в единицу времени определяются формулой:

Полученное выражение содержит сумму двух слагаемых. Первое слагаемое определяется постоянной составляющей затрат и представляет собой обратно пропорциональную зависимость от Т. Второе слагаемое определяется переменной составляющей затрат и представляет собой прямо пропорциональную зависимость от Т.

При коротких циклах Т (частые поставки небольшими партиями) затраты будут значительными за счет первого слагаемого. При длинных циклах Т (редкие поставки крупными партиями) – за счет второго. Сумма этих слагаемых достигает минимума при некоторой промежуточной длине цикла .

Чтобы рассчитать оптимальный цикл , достаточно продифференцировать полученное выражение для затрат L и приравнять производную нулю. Получим:

Откуда

Так как значение Т со знаком «-» не имеет смысла, то в качестве оптимальной длины цикла получаем единственную величину:

Для оптимального размера партии получаем:

Оптимальный размер партии в этих условиях называется также экономичным объемом заказа EOQ (economic order quantity).

Для получения минимальных средних затрат в единицу времени следует подставить в указанную выше формулу для L. В результате получим:

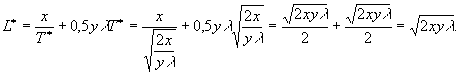
Отметим, что два слагаемых, соответствующих постоянной и переменной составляющей затрат, оказались равны друг другу (это хорошо видно на предпоследнем шаге преобразований). Таким образом, минимум затрат соответствует балансу постоянной и переменной составляющей. Точка минимума общих затрат лежит прямо над точкой пересечения линий постоянных и переменных затрат [2]. Полученные формулы для называются формулами Уилсона.

Пример. Предположим, что магазин продает в среднем 100 коробок конфет в день, затраты на доставку партии конфет в магазин составляют 200 тенге, затраты на хранение конфет оцениваются в 10 тенге за коробку в день. Требуется рассчитать оптимальный размер поставки.

Согласно формулам Уилсона оптимальный размер партии будет равен:

(коробки).

Литература:

1. Чернов В.П., Эйсснер Ю.Н., Чернов А.В. Моделирование управленческих решений. СПб., 2006. – 253с.

2. А.И. Карасев, Н.Ш. Кремер, Т.И. Савельева. Математические методы и модели в планировании. Москва, 1987. – 263с.