Дифференциальные и интегральные уравнения.

к.ф.-м.н. М. С. Алборова

Московский государственный университет технологий и управления. Россия

Теорема вложения для анизотропных пространств Соболева.

In this article are studied the remark on the imbedding theorem of Sobolev spaces.

В данной работе получены некоторые функционально-геометрические условия наложенные на область обеспечивающие теоремы вложения для анизотропных функциональных пространств.

Пусть R-евклидово пространство точек x = (x,….,x), = (l , …..,l) - мультииндекс , l > 0.

Рассмотрим однопараметрическую группу преобразований R

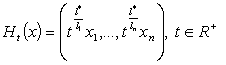
где и гладкую H - однородную метрику, определяемую вектором , r : \{0} R, r(H(x)) = tr(x), x R, непрерывную на R.

Шаром с центром в точке радиуса называется множество

B(x) = {y R : r(x, y) < }.

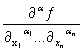Пусть R - открытое подмножество, p 1. Будем говорить, что функция ƒ L(), принадлежит классу если функция имеет обобщенные производные Dƒ L(), = 1. Здесь Dƒ= , и = . Для таких функций определим полунорму:

Пространством назовем замыкание в норме

множества - бесконечно дифференцируемых функций с носителями в

Пусть e- замкнутое множество. Емкостью множества e назовем величину

,

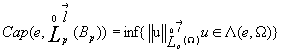где в окрестности e }

Пусть e- компактное подмножество шара B.Будем говорить ,что e - -несущественное подмножество B, если

, , или ,,

где - достаточно малая константа зависящая только от ,.

Совокупность всех-несущественных подмножеств шара Bобозначим через .

Введем пространство

Пусть -пополнение пространства по норме ,

где p>1, - открытое подмножество R и - мера в .

Основными результатами данной работы являются следующие результаты.

Лемма. Для любой функции верно неравенство ,

где - мера в , инфинум берется по всем компактным множествам , таким, что ( - произвольная постоянная).

Пусть - произвольное открытое множество в R и - мера в . Через обозначим множество всех шаров , пересечения которых с - несущественны.

Введем число

.

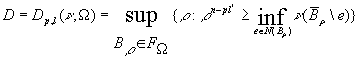Очевидно D неубывающая функция.

Теорема. Пусть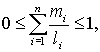

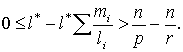
Тогда:

1) Неравенство

(1)

верно для всех в том, и только в том случае, если существуют такие положительные постоянные и k, что для всех шаров из и всех компактов E из

.

2) для наименьшей константы в неравенстве (1) справедливы оценки

.

Литература.

1.Мазья В.Г. Пространства С.Л. Соболева. Изд.Ленингр. ун.,1985,416

2.Бесов О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы вложения,М.,1975.

3.Алборова М.С. ,Водопьянов С.К. Устранимые особенности для решения квазилинейных –квазиэллиптических уравнений. Сиб.Мат.журнал, 1992, т34, №4, с.3-14.