Математика/5. Математическое моделирование

Д.т.н. Карпов В.В., к.ф.м.н. Рябикова Т.В.

Санкт-Петербургский государственный архитектурно-строительный университет

Моделирование оболочек вращения в единой системе координат

Различные виды оболочек (цилиндрические, конические, сферические, торообразные) задаются в разных системах координат, но координатные линии проходят по линиям главных кривизн оболочки [1-4].

Различие оболочек проявляются, в основном, в геометрических соотношениях, которые в срединной поверхности оболочки (в координатной поверхности для ребристых оболочек) имеют вид (для оболочек вращения и это учтено)

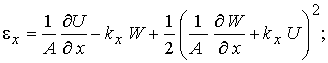
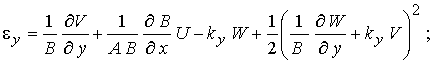(1)

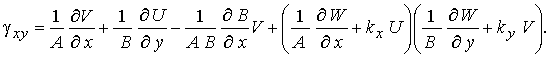
Функции изменения кривизн и кручения при учете поперечных сдвигов (модель Тимошенко-Рейснера) имеют вид

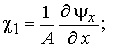
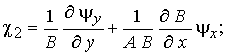(2)

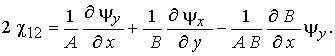
В выражениях (1), (2) координаты могут быть как линейные, так и угловые, а параметры Ляме для различных оболочек разные, но, .

Так, для пологих оболочек прямоугольного плана - линейные координаты, , , 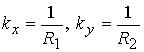причем - константы.

Для цилиндрических и конических оболочек координата – линейная, а – угловая. Для цилиндрических оболочек , , ( – радиус цилиндрической поверхности, является константой). Для конических оболочек , (- угол конусности), ,.

Для сферических и тороидальных оболочек координаты – угловые. Для сферических оболочек ( – радиус сферической поверхности, является константой). Для торобразных оболочек при отступе сектора вращения от оси вращения на и смещении вращающегося сектора от оси вращения на угол , , , , ( 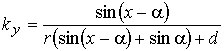– радиус вращающегося сектора, является константой).

Введем безразмерные параметры:

, , , , , , ,

, , , , , .

Деформации в безразмерных параметрах принимают вид

,

,

,

,

,

,

,

.

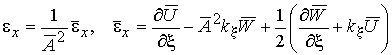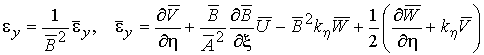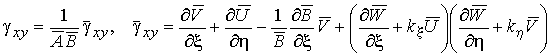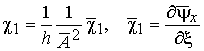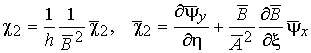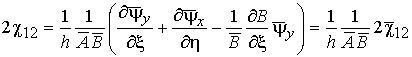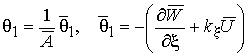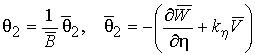Функционал полной энергии деформации оболочки принимает вид

,

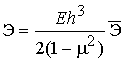где

.

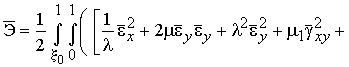
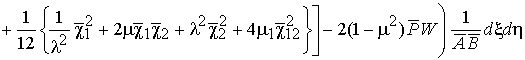Даже при переходе к безразмерным параметрам в выражении каждый член умножается на обратную величину произведения параметров Ляме, что делает это выражение громоздким.

Перейдем к линейным координатам, совпадающим с линиями главных кривизн, как это сделано для пологих оболочек прямоугольного плана (оболочек переноса), тогда функционал полной энергии деформации оболочек вращения упроститься.

Для перехода к общей системе координат сделаем замену переменных Теперь координаты – линейные координаты, проходящие по линиям главных кривизн оболочки.

Если координаты имели постоянные пределы изменения , , то теперь координата имеет постоянные пределы изменения, а координата имеет верхний предел изменения, зависящий от .

Таким образом, так как , , обратные соотношения имеют вид , .

В соотношениях (1), (2), где , , , , , перейдем к новым координатам , имея в виду, что, например, .

Тогда

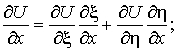
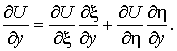
Так как , , ,, 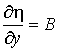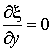то

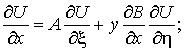
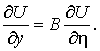(3)

Таким образом, имеем следующие формулы для перехода к новым координатам

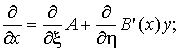
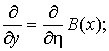
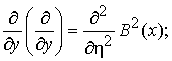
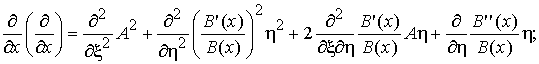
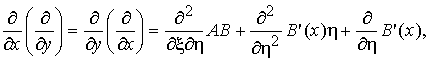
где .

Для модели Тимошенко-Рейснера в функционале полной энергии деформации встречаются только первые производные искомых функций, а для модели Кирхгофа-Лява – и вторые производные. Так как формулы перехода к новым координатам для вторых производных громоздкие, то использовать модель Кирхгофа-Лява не целесообразно.

Учитывая (3) геометрические соотношения (1) принимают вид

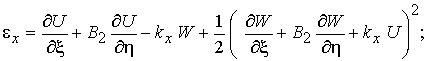
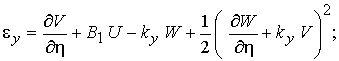(4)

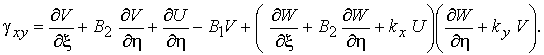
Функции изменения кривизн и кручений (2) примут вид

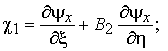
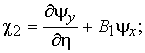
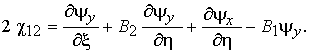(5)

В соотношениях (4), (5) , .

В таблице для различных видов оболочек представлены значения, входящих в соотношения (4), (5) параметров в новых координатах (так как , то в таблице этот параметр не представлен).

После перехода к новым координатам в функционале полной энергии деформации, учитывая, что Якобиан перехода будет равен, получим

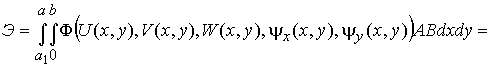
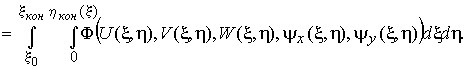(6)

В таблице .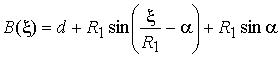

Таким образом, при переходе к единой системе координат для оболочек вращения изменяются только геометрические соотношения, в которых будут присутствовать два коэффициента и , разных для различных видов оболочек. Сами геометрические соотношения упрощаются. Так же существенно упрощается функционал полной энергии деформации.

В MATLAB7 была составлена программа для расчета оболочек вращения в единой системе координат для геометрически линейной задачи (в выражениях деформаций (1) пренебрегали квадратичными членами). В качестве примера рассматривалась панель сферической оболочки, радиуса , ограниченная углами и (рис. 1).

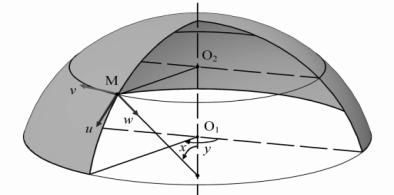
Рис. 1. Общий вид сферической оболочки

В новой системе координат для панели сферической оболочки , , , , , 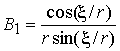при этом прямоугольная область интегрирования перешла в криволинейную трапецию .

Для нахождения функций перемещений и поворотов, обеспечивающих минимум функционалу полной энергии деформации (6), применяем процедуру метода Ритца, согласно которой приближенное решение поставленной задачи будем искать в виде

, ,

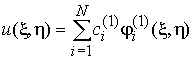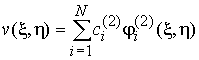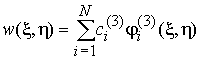, (7)

, .

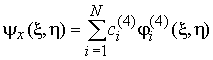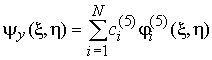Здесь – известные базисные функции переменных и , удовлетворяющие заданным краевым условиям на границе области ; – неизвестные числовые параметры, определяемые из условия минимума функционала (6).

В качестве базисных функций, удовлетворяющих условиям жесткой заделки на краях оболочки, использовались многочлены:

, .

На рисунках 2 и 3 приведены графики функции прогибов и интенсивности напряжений в единой системе координат для сферической оболочки с исходными данными: , , , , , , , при нагрузке . В разложении (7) по методу Ритца .

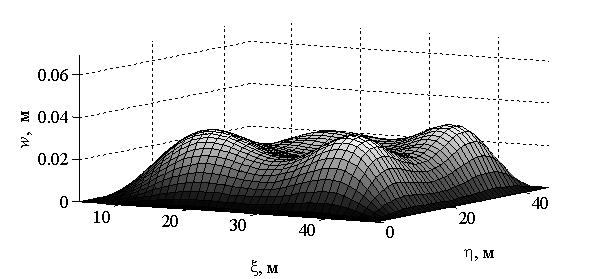
Рис. 2. Распределение прогибов оболочки в единой системе координат ,

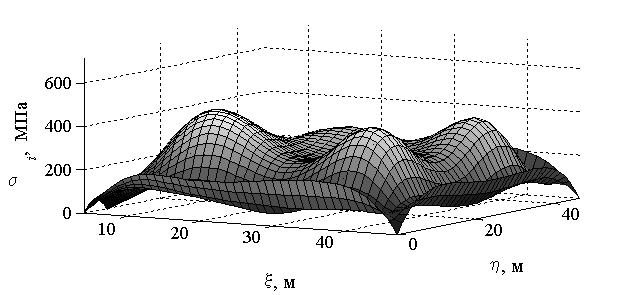
Рис. 3. Распределение интенсивности напряжений оболочки

в единой системе координат ,

Максимальные значения функции прогиба и интенсивности напряжений соответственно равны и . Для сравнения был проведен расчет данной оболочки в сферической системе координат и . На рисунках 4 и 5 представлены функции и , при этом максимальные значения прогиба и интенсивности напряжений оказались равными: и .

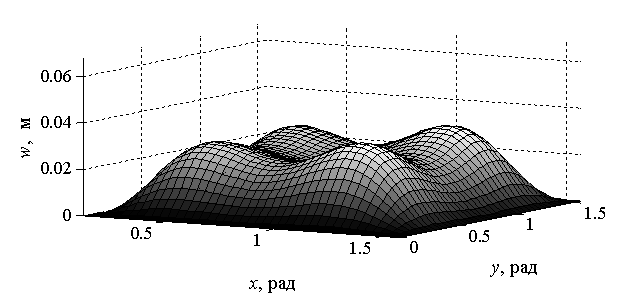
Рис. 4. Распределение прогибов оболочки в сферической системе координат ,

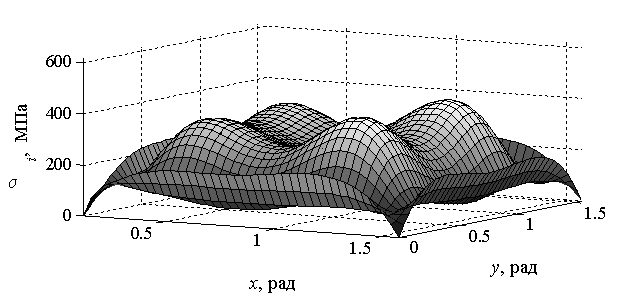
Рис. 5. Распределение интенсивности напряжений оболочки

в сферической системе координат ,

Таким образом, процесс программирования задачи в единой системе координат существенно упрощается, причем для различных видов оболочек будут отличаться только коэффициенты , . Результаты расчета напряженно-деформированного состояния оболочек, полученные в единой системе, практически совпали с результатами, полученными в исходной системе координат

Литература:

1. Векуа И.Н. Некоторые общие методы построения теории оболочек. – М.: Наука. 1982. – 286 с.

2. Гольденвейзер А.Л. Теория упругих тонких оболочек. – М.: Гостехиздат, 1953.

3. Лурье А.И. Общая теория упругих тонких оболочек // ПММ. Т.4, 1940. Вып.2.

4. Новожилов В.В. Теория тонких оболочек. – Л.: Судпромиздат, 1962. – 431 с.