Несуществование дополнительных аналитических первых интегралов возмущённой задачи Баррара.

Севрюков П. Ф.                                                                    г. Ставрополь

 

Рассмотрим движение спутника, принимаемого за материальную точку, в поле тяготения осесимметричной планеты. Если ось аппликат направить вдоль ось динамической симметрии планеты, а начало координат поместить в произвольной точке этой оси, то гравитационный потенциал в стандартных обозначениях будет иметь вид

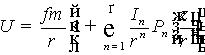,                                           (1)

где f – гравитационная постоянная, т – масса планеты, r – модуль радиус-вектора, In – постоянный параметр, Рn – полином Лежандра n – го порядка.

Гравитационное поле планеты будем аппроксимировать полем тяготения Баррара [1, 2]. При этом начало координат поместим в шаровую точку инерции планеты, тогда I1=с. Это значение составляет аппликату центра масс планеты, I2=0, а потенциал Баррара запишется следующим образом:

,                                         (2)

где sinφ=. Оставшиеся члены гравитационного потенциала составят пертурбационную функцию

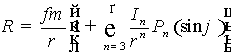,                                               (3)

U=W+R.                                                   (4)

Уравнение движения невозмущённой задачи Баррара интегрируется в замкнутом виде в квадратурах. Канонические переменные «действие-угол» введены в работе [2] и выражены через эллиптические квадратуры. Дифференциальные уравнения возмущённой задачи Баррара принимают наиболее простую форму, если ввести канонические переменные L, G, H, l, g, h, подобные элементам Делоне кеплеровского движения и обращаются в соответствующие элементы при с=0 [3]. Уравнения возмущённого движения в канонических оскулирующих переменных L, G, H, l, g, h будут иметь вид

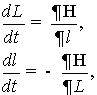
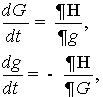
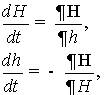                                  (5)

причём

.                                             (6)

Ясно, что в формуле (6)  - невозмущённый гамильтониан задачи Баррара, R – пертурбационная функция(3), которая с учётом соотношений

sinφ=sini∙cosθ,                                           (7)

r=p                                           (8)

может быть представлена в форме

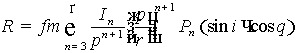.                        (9)

В приведённых формулах р=а(1-е2), θ=v+ω; а- большая полуось, е – эксцентриситет, i – наклон орбиты, v – истинная аномалия, ω – аргумент перицентра.

Введём функции наклона и эксцентриситета для задачи Баррара [4]:

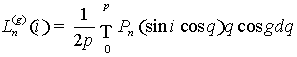,                        (10)

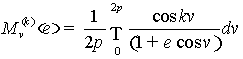,                                   (11)

тогда пертурбационная функция запишется в виде

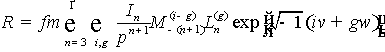.                         (12)

Функции эксцентриситета связаны с коэффициентами Ганзена с нулевым верхним индексом соотношением

.                                                 (13)

Функции наклона выразятся через присоединённые функции Лежандра:

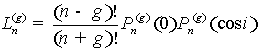.                                (14)

Выбрав в качестве малого параметра величину μ=c10-6, где r0 – средний радиус планеты, представим пертурбационную функцию рядом

.                                                     (15)

Используя формулы связи, указанные в работе [3], выразим элементы орбиты а, е, i через переменные действия L, G, H. Для угловых переменных с точностью до ε2 v=l, ω=g. Здесь . Таким образом, каждая функция  может быть выражена через переменные L, G, H, l, g и является периодической по угловым переменным l и g с периодом 2π:

.                            (16)

В соответствии с [3] невозмущённый гамильтониан задачи имеет вид

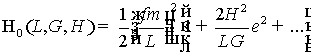.                     (17)

Нетрудно заметить, что угловая переменная h является циклической, поэтому уравнения Гамильтона (5) допускают первый интеграл

=L=const,                                                     (18)

что даёт возможность понизить порядок первоначальной системы уравнений и получить приведённую систему

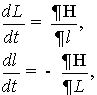
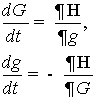                                              (19)

с гамильтонианом

.                             (20)

В «Новых методах небесной механики» А. Пуанкаре [5] доказана теорема, которая в нашем случае может быть сформулирована следующим образом:

Пусть движение спутника описывается приведённой системой (19), причём гамильтониан имеет вид (20). Тогда, если

- функция  не зависит от угловых переменных l и g,

- гессиан функции  по переменным L и G не равен тождественно нулю,

- функции  являются периодическими функциями от l и g с периодом 2π,

то приведённая система уравнений не допускает никаких других независимых аналитических первых интегралов, кроме интеграла энергии =const при достаточной малости параметра μ.

Нетрудно проверить, что все условия сформулированной теоремы выполняются. Доказательство основывается на том факте, что если бы в задаче существовал однозначный интеграл, то в разложении пертурбационной функции в кратный ряд Фурье по угловым переменным все коэффициенты должны были бы обращаться в нуль. Изучение разложения R показывает, что всё это не так. Следовательно, мы должны сделать вывод о том, что приведённая система уравнений (19) не может иметь никаких аналитических однозначных интегралов, не являющихся следствием интеграла энергии и циклического интеграла (18).

Библиографический список.

1.          Barrar R.B. Some remarks on the motion of a satellite of an oblate planet.// Astron. Journ. 1961. V. 66, №1.

2.          Дёмин В.Г. Движение искусственного спутника в нецентральном поле тяготения./ М.: Наука, 1968. стр. 122-130.

3.          Искакова А.М. Переменные «действие-угол» в задаче Баррара.// Аналитическая механика тел переменной массы. Алма-Ата, 1982. стр. 30-36.

4.          Севрюков П.Ф. О дополнительных аналитических первых интегралах возмущённой задачи Баррара.// Проблемы механики управляемого движения. Нелинейные динамические системы: Межвуз. сб. научн. трудов/ Пермь: – Перм. ун-т, 1989. стр. 142-145.

5.          Пуанкаре А. Новые методы небесной механики// Пуанкаре А. Избранные труды/ М.: Наука, 1971. т. 1, стр. 8-326.