Технические науки / металлургия
Косенко В.М.,
Глущевський В.В., Іванов В.І., Мосейко Ю.В.
Запорізька державна
інженерна академія
Про оптимізацію складу доДАВАНЬ флюсІВ дО ШИХТИ вторинної
свинцевої плавки
Одним з найважливіших аспектів вдосконалення металургійного виробництва є
його оптимізація, яка дозволяє забезпечити підвищення ступеня витягання цінних
металів за рахунок зміни речового складу сировини і добавок флюсів.
Технологія пірометалургійного виробництва важких кольорових
металів характеризується високим виходом шлаків відносно виплавленого металу. І
хоча вміст важких кольорових металів у шлаку складає 0,1.2,0 % величина їх
загальних втрат є достатньо суттєвою величиною.
Завданням досліджень є оптимізація складу додавань флюсів до шихти
вторинної свинцевої плавки. що дозволяє мінімізувати втрати даного металу із
шлаком за різних комбінацій вхідних параметрів процесу (складу шлаку,
температури плавлення, тривалості витримки розплаву в печі та витрати
відновника).
Статистичну залежність між вмістом свинцю у шлаку Y і вхідними
параметрами процесу визначали у формі моделі множинної лінійної регресії:
,
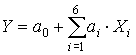(1)
де 
– вектор невідомих
параметрів регресії; 
– значення і-го
чинника: Х1, Х2, Х3 – змінювання в шлаку
вмісту SiO2 (31…40 %), FеO (31…40 %) і CаO (31…40 %); Х4 – температура плавлення (1250…1300 °С); Х5 – тривалість витримки
розплаву в печі (45…60 хвил.); Х6
– витрата відновника (9…11 %).
Невідомі параметри регресії аі обчислювали методом
найменших квадратів з використанням статистичної бази, сформованої за
результатами проведення численних експериментів (табл. 1).
Таблиця 1 – Статистична база
моделювання
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Y |
|
40 |
24 |
24 |
1300 |
60 |
11 |
2,4 |
|
40 |
20 |
24 |
1250 |
60 |
9 |
1,4 |
|
31 |
24 |
24 |
1250 |
45 |
9 |
1,2 |
|
40 |
24 |
15 |
1300 |
45 |
9 |
2,3 |
|
31 |
20 |
24 |
1300 |
45 |
11 |
0,9 |
|
40 |
20 |
15 |
1250 |
45 |
11 |
1,6 |
|
31 |
24 |
15 |
1250 |
60 |
11 |
2,0 |
|
31 |
20 |
15 |
1300 |
60 |
9 |
1,9 |
Значення коефіцієнта множинної детермінації (R2 = 0,9841), яке визначали для моделі
регресії, свідчить про те, що теоретичні значення результуючого показника Y із достатньою точністю
співпадають з його фактичними значенням для кожного експерименту.
Як результат обробки результатів експериментів одержали рівняння регресії
вигляду:
(2)
Перевірка одержаної моделі на адекватність із використанням критерію Фішера
показала, що його розрахункове значення (Fр = 10,333) більше
табличного значення (Fтабл = 2,699) для заданого рівня
ймовірності Р = 0,95 і відповідних мір свободи k1 = 6 і k2 = 17.
Статистичну значимість параметрів a1…a6 моделі регресії (1) оцінювали із
застосуванням t-статистики Ст’юдента.
Результати розрахунків представлені в табл. 2.
Таблиця 2 - Перевірка параметрів моделі регресії (1) на значущість
|
Статистичний показник |
Значення
статистичного показника для чинника |
||||||
|
вільний член |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
|
|
|
-11,7222 |
0,0472 |
0,1313 |
-0,0528 |
0,0065 |
0,0283 |
0,0125 |
|
|
3,3964 |
0,0139 |
0,0313 |
0,0139 |
0,0025 |
0,0083 |
0,0625 |
|
|
3,4514 |
3,4 |
3,4 |
3,8 |
2,6 |
3,4 |
0,2 |
Табличне значення t-статистики для рівня ймовірності Р
= 0,95 і кількості мір свободи k1 = 17 складає tтабл = 2,1098. З табл. 2
видно, що для всіх параметрів регресії, окрім параметра а6, встановлено значущий вплив
чинників Х1, Х2, Х3, Х4 і Х5 на показник Y та їх слід враховувати під час
розрахунків.
Запропонована модель дозволяє здійснювати варіювання вмісту оксидів
кальцію, заліза, кремнію й алюмінію у шлаку шахтної свинцевої плавки, а також тривалості
витримки розплаву в печі для одержання мінімальних втрат металу із шлаком. При
цьому виключаються витратні лабораторно-промислові випробування, а також
витрати на додаткову переробку силікатних відходів з метою одержання шлаків,
придатних для застосування у промисловому та цивільному будівництві.