Технические науки/ 6.Электротехника и радиоэлектроника

Герасина А.В., Варварюк М.В.

ГВУЗ «Национальный горный университет», Украина

Выбор структуры модели телекоммуникационного трафика

При проектировании и обслуживании информационных телекоммуникационных систем и сетей одной из основных проблем является задача обеспечения качества обслуживания при обработке потока данных – трафика, что является следствием информационного обмена между системами. В этих условиях разработка новых сетевых технологий и повышение эффективности работы современных телекоммуникационных систем и сетей требуют создания математических моделей трафика, которое выполняется с помощью процедуры его идентификации.

При решении задачи идентификации актуальной проблемой является выбор структуры модели, а также базисных функций.

Нами была оценена эффективность моделей телекоммуникационного трафика при вариации блочно-ориентированных типов структур – Винера, Гаммерштейна, Гаммерштейна-Винера и авторегрессии с дополнительным входным сигналом (ARX) [1]. В качестве базисных функций использовались каскадные нейронные сети (НС), вейвнеты (НС с функциями активации в виде вейвлет) и полиномы Колмогорова-Габора.

Моделирование выполнялось в среде Matlab для экспериментальных данных, которые представляют собой нагрузку на некоторую телекоммуникационную сеть в течение месяца. Глубина прогноза составляла такта, а глубина памяти – 3 такта. В качестве критерия оценки моделей выбран критерий относительной среднеквадратичной ошибки.

Результаты идентификации телетрафика со структурой модели ARX и базисными функциями в виде вейвнета и каскадной НС приведены на рис. 1. При этом значения относительной среднеквадратичной ошибки составили 0,0443 для вейвнета и 0,1293 для каскадной НС.

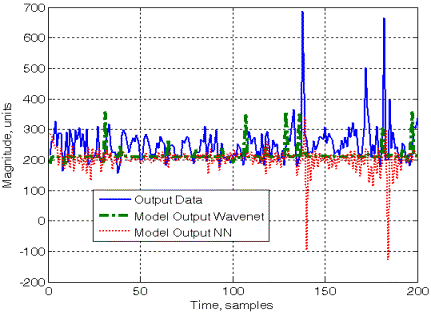
Рис. 1. Результаты идентификации телекоммуникационного трафика

в виде модели ARX

В результате идентификации телетрафика со структурой модели Гаммерштейна-Винера и базисными функциями в виде вейвнета и полинома Колмогорова-Габора получены значения относительной среднеквадратичной ошибки, которые составили 0,0702 для вейвнета и 0,2625 для полинома Колмогорова-Габора.

В результате идентификации телетрафика с базисными функциями в виде вейвнет и со структурами моделей Винера и Гаммерштейна получены значения относительной среднеквадратичной ошибки, которые составили: для моделей Винера – 0,0642, Гаммерштейна – 0,0502.

Таким образом, в результате проведенных исследований установлено, что в качестве структуры модели телетрафика предпочтительной является структура ARX, поскольку она дает меньшие значения среднеквадратичной ошибки при различных базисных функциях. В качестве базисных функций рекомендуется использовать вейвнеты.

Дальнейшие исследования должны быть направлены на параметрическую идентификацию телекоммуникационного трафика в классе его интеллектуальных прогнозирующих моделей с базисными функциями в виде вейвнет.

Литература:

1. Ljung L. Identification of Nonlinear Systems / L. Ljung // Proceeding of the IEEE. – 2006. – № 6. – P. 1-10.