УДК 517.52/524:517/58/589

 

О.Ю.Тарновецька

 

СУММИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ МЕТОДОМ КОНЕЧНОГО ГИБРИДНОГО ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ ТИПА ХАНКЕЛЯ 1-ГО РОДА–ЛЕЖАНДРА 2-ГО РОДА

 

Рассмотрим задачу построения ограниченного на множестве I1 = {r: r Î (0, R1)  (R1, R2), R2 < ¥} решения сепаратной системы дифференциальных уравнений Бесселя и Лежандра для модифицированных функций

                               , r Î (0, R1),                              

                              , r Î (R1, R2)                                 (1)

по условиям сопряжения

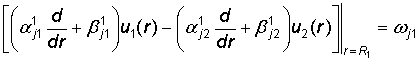            , j = 1, 2               (2)

и краевым условиям

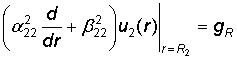                        = 0, .                          (3)

          В системе (1) принимают участие дифференциальные операторы Бесселя Bn, a [1] и Лежандра L(m) [2]

,.

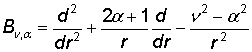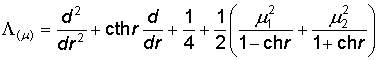          Мы предполагаем, что выполнены условия на коэффициенты:

 ³ 0,  ³ 0,  ¹ 0, , c11c21 > 0, n ³ a ³ 1/2,

m1 ³ m2 ³ 0, qj > 0; j, k, m = 1, 2, (m) = (m1, m2).

          Фундаментальную систему решений для уравнения Бесселя (Bn, a – )v = 0 образуют модифицированные функции Бесселя 1-го рода

In, q (q1r) и 2-го рода Kn, q (q1r) [1]; фундаментальную систему решений для уравнения Лежандра  образуют обобщенные присоединенные функции Лежандра 1-го рода и 2-го рода  [2]; n2 = –1/2+q2 [2].

          Наличие фундаментальной системы решений дает возможность построить общее решение краевой задачи (1)–(3) методом функций Коши [3, 4]:

          u1(r) = A1In ,a(q1r) + ,

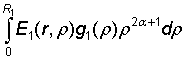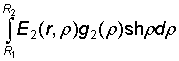          u2(r) = A2 + B2 + .                   (4)

          Здесь Ej(r, r) – функции Коши [3, 4]:

                                 ,

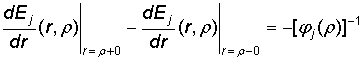                       ,                          (5)

j 1(r) = r2a + 1, j 2(r) = sh r.

          Введем в рассмотрение функции:

,

,

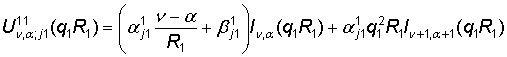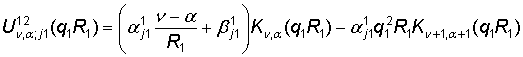, j =1, 2.

          Непосредственно проверяется, что функция Коши

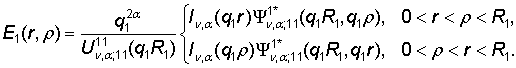                    (6)

          Определим функции:

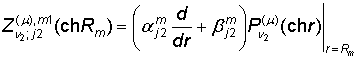, m = 1, 2,

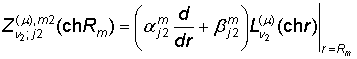, j = 1, 2,

,

.

          Непосредственно проверяется, что функция Коши

           ´

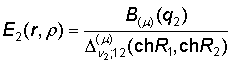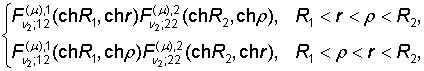          ´                           (7)

          .

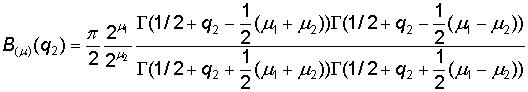          Условия сопряжения (2) и краевое условие в точке r = R2 для определения величин A1, A2, B2 дают алгебраическую систему из трех уравнений:

                ,

                ,              (8)

                .

          Здесь принимает участие функция

G12 =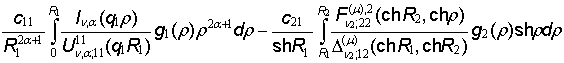     

          Предположим, что выполнено условие однозначной разрешимости краевой задачи (1) – (3): для любого вектора  = {q1; q2} ¹  определитель алгебраической системы (8)

 –   ¹ 0. (9)

          Введем в рассмотрение главные решения краевой задачи (1) – (3): 1) порожденные неоднородностью условий сопряжения функции Грина

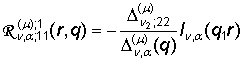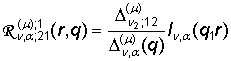, ,                       (10)

, ;

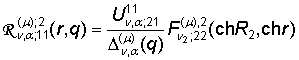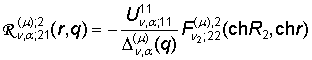2) порожденные краевым условиям в точке r = R2 функции Грина

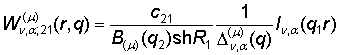, q = (q1, q2),                                 (11)

;

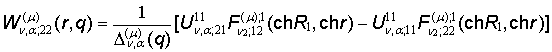3) порожденные неоднородностью системы (1) функции влияния

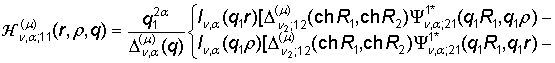
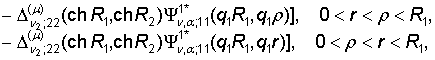
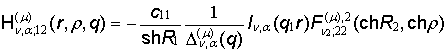,                               (12)

,

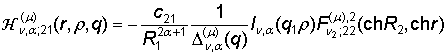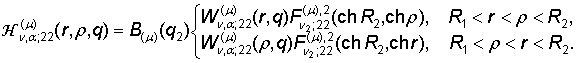
          В результате однозначной разрешимости алгебраической системы (8) и подстановки найденных значений A1, A2, B2 в формулы (4) имеем единственное решение краевой задачи (1) – (3):

               uj(r) =  +  +  +

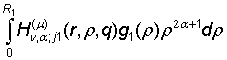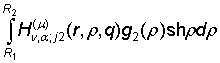          +  + , j = 1, 2. (13)

          Построим теперь решение краевой задачи (1) – (3) методом интегрального преобразования, порожденного на множестве I1 гибридным дифференциальным оператором (ГДО)

           = q(r)q(R1 – r)Bn, a + q(r – R1)q(R2 – r)L(m), q(x) =         (14)

q(x) – единичная функция Хевисайда [4].

          Так как ГДО  не имеет на множестве I1 особых точек и самосопряженный, то его спектр действительный и дискретный.

          Собственные элементы ГДО  (спектр и соответствующую ему спектральную функцию) найдем как решение спектральной задачи Штурма-Лиувилля: найти ненулевое решение системы уравнений

                                      , r Î (0, R1),                                     

                                     , r Î (R1, R2)                                      (15)

по краевым условиям

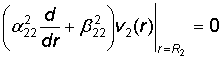                         = 0,                          (16)

и условиям сопряжения

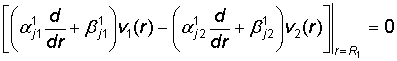              , j = 1, 2               (17)

          Здесь bj = ()1/2,  ³ 0, b – спектральный параметр.

          Фундаментальную систему решений для дифференциального уравнения Бесселя (Bn, a + )v = 0 образуют функции v1 = Jn, a (b1r) и v2 = Nn, a (b1r) [1]; фундаментальную систему решений для обобщенного дифференциального уравнения Лежандра  образуют функции v1 =  и v2 = .

          Если предположить, что спектральная функция

          (r, b)  = q(r)q(R1 – r) (r, b) + q(r – R1)q(R2 – r)(r, b)

и положить

           = A1 Jn, a, (b1r), (r, b) = A2 + B2,

то условия (16), (17) для определения A1, A2, B2 дают однородную алгебраическую систему уравнений:

 = 0, j = 1, 2,

 = 0.                                                 (18)

          Алгебраическая система уравнений (18) имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю [5]:

      (19)

          В равенствах (18), (19) принимают участие функции

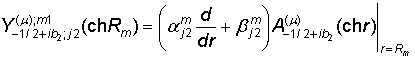          , m, j = 1, 2,

          ,

          ,

           –

          – .

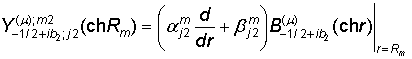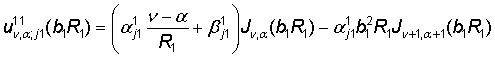          Корни bn трансцендентного уравнения (19) образуют дискретный спектр ГДО : .

          В результате решения системы (18) стандартным способом [5] получаем величины A1, A2 и B2, а с ними функции

          (r, bn) = 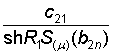Jn, a (b1nr), bjn =  ()1/2, j = 1, 2,

          (r, bn) =  – .          (20)

          Здесь приняты обозначения:

 = ,

S(m)(b2n) = ,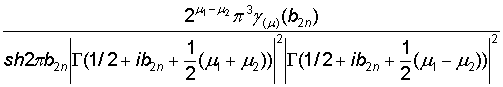

g(m)(b2n) = (cosm1p sh2pb2n) (cosm2p + cosm1p × ch2pb2n)–1, j = 1, 2,                        

          Наличие спектральной функции (r, bn) с квадратом нормы

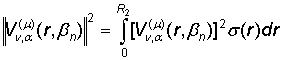                               ,                                (21)

и весовой функции

                  s (r) =q(r)q(R1 – r)s1r2a + 1 + q(r – R1)q(R2 – r) s2 sh r,

, s2=1, дает возможность определить прямое  и обратное  конечное гибридное интегральное преобразование типа Ханкеля 1-го рода-Лежандра 2-го рода, порожденное на множестве I1 ГДО  [6]:

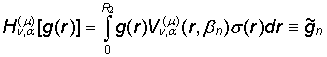                           ,                            (22)

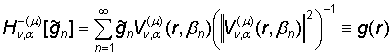                    .                     (23)

          Единственное решение краевой задачи (1) – (3), построенное методом конечного гибридного интегрального преобразования (22), (23) по известной логической схеме [6], имеет структуру:

          uj(r) =  +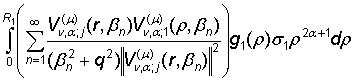

                     +  +

+  + –

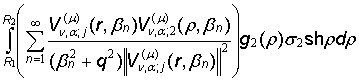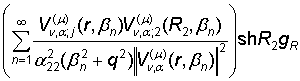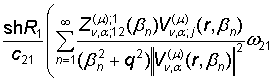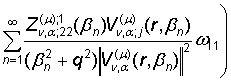             – , q2 = max{; }, j = 1, 2;

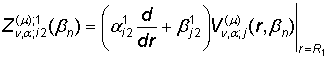          , i = 1, 2.

          Сравнивая в силу единственности решения (13) и (24), имеем такие формулы суммирования полипараметрических функциональных рядов::

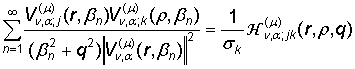          , j, k = 1, 2,                       (25)

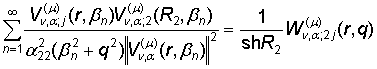          , j = 1, 2,                      (26)

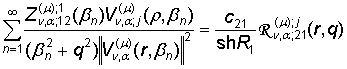          , j = 1, 2,                            (27)

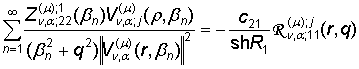          , j = 1, 2.                          (28)

          Функции влияния  определены равенствами (12), функции Грина  – равенствами (11), а функции Грина условиям сопряжения  – равенствами (10).

          Итогом изложенного выше есть утверждение.

          Теорема. Если функция f(r) = {Bn, a[g1(r)]; L(m) [g2(r)]} непрерывная на множестве I1, функции gj(r) удовлетворяют условиям сопряжения (2) и краевые условия (3), и выполняется условие (9) однозначной разрешимости краевой задачи (1) – (3), то имеют место формулы (25) – (28) суммирования полипараметрических функциональных рядов по собственным элементам ГДО , определенного равенством (14).

 

          ЛІТЕРАТУРА

1.     Ленюк М.П. Исследование основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев, 1982. – 62 с. – (Препринт / АН УССР. Ин-т математики; 83.3).

2.     Конет І.М., Ленюк М.П. Інтегральні перетворення типу Мелера-Фока.  Чернівці: Прут, 2002. – 248 с.

3.     Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.

4.     Шилов Г.Е. Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328 с.

5.     Курош А.Г. Курс высшей алгебры. – М.: Наука, 1971. – 432 с.

6.     Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні інтегральні перетворення, породжені диференціальними рівняннями другого порядку. – Чернівці: Прут, 2001. – 228 с.