М.П.Ленюк
Чернівецький факультет НТУ „ХПІ”
Обчислення невласних інтегралів
за власними елементами гібридного диференціального оператора Ейлера-Бесселя на
полярній вісі r ³ R0 > 0
Розглянемо
задачу про конструкцію обмеженого на множині ![]() = {r: r Î (R0, R1)
= {r: r Î (R0, R1) ![]() (R1, ¥)} розв’язку сепаратної
системи диференціальних рівнянь Ейлера та Бесселя
(R1, ¥)} розв’язку сепаратної
системи диференціальних рівнянь Ейлера та Бесселя
![]() , r Î (R0, R1),
, r Î (R0, R1),
![]() , r Î (R1, ¥) (1)
, r Î (R1, ¥) (1)
за крайовими умовами
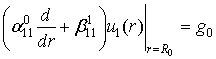 ,
, ![]() = 0 (2)
= 0 (2)
та умовами спряження
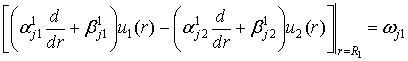 , j = 1, 2. (3)
, j = 1, 2. (3)
У рівностях (1) беруть участь диференціальні
оператори Ейлера ![]() [1] та Бесселя
[1] та Бесселя ![]() [2]:
[2]:
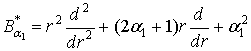 , 2a1 + 1 > 0,
, 2a1 + 1 > 0,
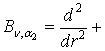
![]()
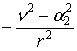 , n ³ a2 > –1/2.
, n ³ a2 > –1/2.
Вважаємо, що виконані умови на коефіцієнти: qj > 0, ![]() ,
, ![]() , |
, |![]() | +
| + ![]() ¹ 0,
¹ 0, ![]() ³ 0,
³ 0, ![]() ³ 0, с21 × c11 > 0, cj1 =
³ 0, с21 × c11 > 0, cj1 = ![]() .
.
Фундаментальну
систему розв’язків для рівняння Ейлера ![]() утворюють функції v1 =
утворюють функції v1 = ![]() та v2 =
та v2 = ![]() [1]; фундаментальну
систему розв’язків для рівняння Бесселя
[1]; фундаментальну
систему розв’язків для рівняння Бесселя ![]() утворюють функції v1 =
утворюють функції v1 = ![]() (q2r) та v2 =
(q2r) та v2 = ![]() (q2r) [2].
(q2r) [2].
Наявність
фундаментальної системи розв’язків дозволяє побудувати розв’язок крайової
задачі (1) – (3) методом функцій Коші [1, 3]:
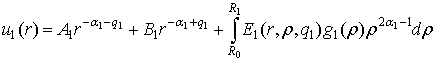 ,
,
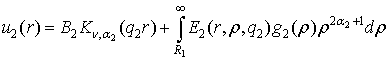 . (4)
. (4)
У рівностях (4) беруть участь функції Коші:
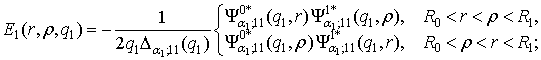 (5)
(5)
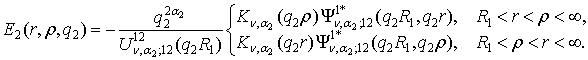 (6)
(6)
У
рівностях (5), (6) прийняті позначення:
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() ,
,
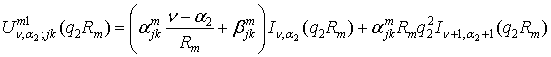 ,
,
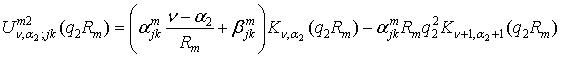
![]() .
.
Крайова
умова в точці r = R0 та умови спряження (3) для визначення величин A1, B1,B2 дають алгебраїчну
систему з трьох рівнянь:
![]() ,
,
![]() ,
,
![]() . (7)
. (7)
У системі (7) бере участь функція
G12 = 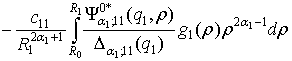 +
+
+ 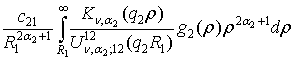 .
.
Припустимо, що виконана умова однозначної розв’язності даної крайової
задачі: для ненульового вектора ![]() = {q1; q2} визначник алгебраїчної системи (7)
= {q1; q2} визначник алгебраїчної системи (7)
![]() , (a) = (a1, a2). (8)
, (a) = (a1, a2). (8)
Визначимо
головні розв’язки крайової задачі (1) – (3):
1) породжені
неоднорідністю системи (1) функції впливу
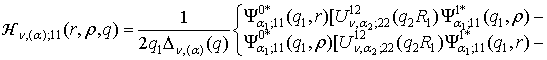
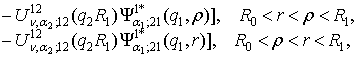
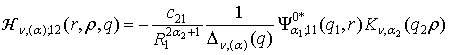 , (9)
, (9)
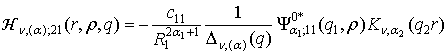 ,
,
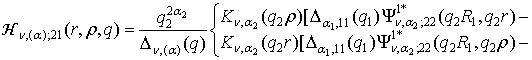
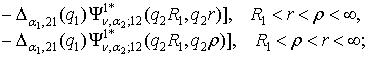
2) породжені крайовою умовою в точці
r = R0 функції Гріна
Wn, (a); 11(r, q)
= 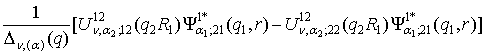 ,
,
Wn, (a); 12(r, q)
= 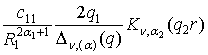 ;
;
3) породжені неоднорідністю умов
спряження функції Гріна
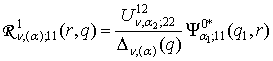 ,
, 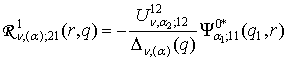 ,
,
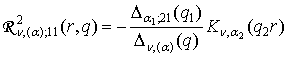 ,
, 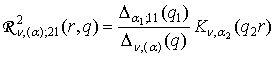 ; (11)
; (11)
У результаті однозначної розв’язності алгебраїчної
системи (7) та підстановки одержаних
значень величин A1, B1 та B2 у формули (4) маємо
єдиний розв’язок крайової задачі (1) – (3):
uj(r) = Wn, (a); 1j(r, q)g0 + ![]() +
+ ![]() +
+
+ 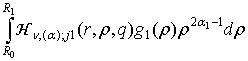 +
+ 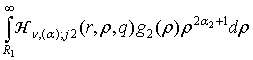 , j = 1, 2. (12)
, j = 1, 2. (12)
Побудуємо розв’язок крайової задачі (1) – (3) методом інтегрального
перетворення, породженого на множині ![]() гібридним диференціальним оператором (ГДО)
гібридним диференціальним оператором (ГДО)
![]() , (13)
, (13)
q(x) – одинична функція Гевісайда [3].
Визначимо
функції та величини:
![]() ,
,
![]() ,
,
![]() , j = 1, 2;
, j = 1, 2;
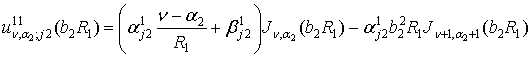 ,
,
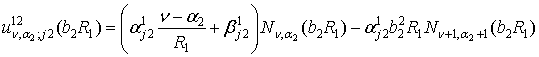 ,
,
bj = (b 2 + ![]() )1/2,
)1/2, ![]() ³ 0, j = 1, 2;
³ 0, j = 1, 2;
![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]() ,
,
![]() ,
, ![]() , Jn(x), Nn(x) – функції Бесселя порядка n [2].
, Jn(x), Nn(x) – функції Бесселя порядка n [2].
Наявність
спектральної функції
Vn, (a)(r, b) = q(r – R0)q(R1 – r)Vn, (a); 1(r, b) + q(r – R1)Vn, (a); 2(r, b),
спектральної щільності
Wn, (a)(b) = b ![]() ([wn, (a); 1(b)]2 + [wn, (a); 2(b)]2)–1
([wn, (a); 1(b)]2 + [wn, (a); 2(b)]2)–1
та вагової функції
s(r) = q(r –
R0)q(R1 – r)s 1![]() + q(r – R1)s 2
+ q(r – R1)s 2![]() ,
, 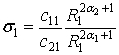 , s2 = 1
, s2 = 1
дозволяє визначити пряме Hn, (a) та обернене ![]() гібридне інтегральне
перетворення, породжене на множині
гібридне інтегральне
перетворення, породжене на множині ![]() ГДО
ГДО ![]() [4]:
[4]:
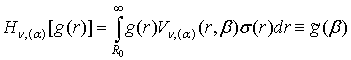 , (14)
, (14)
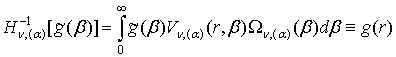 , (15)
, (15)
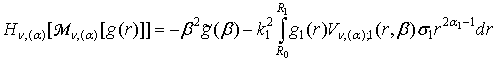 –
–
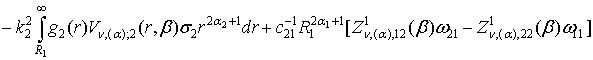 –
–
–
![]() , (16)
, (16)
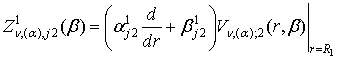 , j = 1, 2.
, j = 1, 2.
Запишемо систему (1) в матричній формі
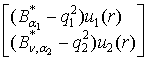 = –
= – ![]() (17)
(17)
Інтегральний оператор Hn, (a) зобразимо у вигляді операторної матриці-рядка:
Hn, (a)[¼] = 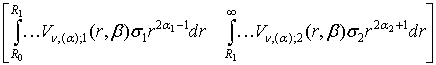 . (18) Припустимо, що max{
. (18) Припустимо, що max{![]() ;
; ![]() } =
} = ![]() > 0. Покладемо всюди
> 0. Покладемо всюди ![]() ,
, ![]() ³ 0. Застосуємо за правилом множення матриць операторну
матрицю-рядок (18) до системи (17). Внаслідок тотожності (16) маємо алгебраїчне
рівняння:
³ 0. Застосуємо за правилом множення матриць операторну
матрицю-рядок (18) до системи (17). Внаслідок тотожності (16) маємо алгебраїчне
рівняння:
![]() +
+
+ ![]() .
.
Звідси
знаходимо, що функція
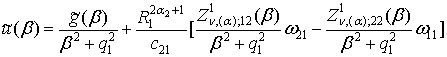 +
+
+ 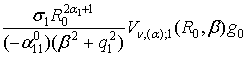 . (19)
. (19)
Інтегральний оператор ![]() згідно правила (15)
як обернений до (18) зобразимо у вигляді операторної матриці-стовпця:
згідно правила (15)
як обернений до (18) зобразимо у вигляді операторної матриці-стовпця:
![]() [¼] =
[¼] = 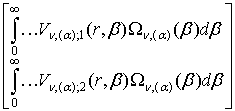 . (20)
. (20)
Застосуємо
за правилом множення матриць операторну матрицю-стовпець (20) до
матриці-елемента [![]() (b)], де функція
(b)], де функція ![]() (b) визначена формулою (19). Після низки елементарних
перетворень маємо єдиний розв’язок крайової задачі (1) – (3):
(b) визначена формулою (19). Після низки елементарних
перетворень маємо єдиний розв’язок крайової задачі (1) – (3):
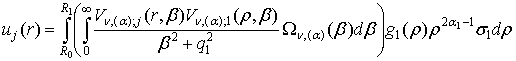 +
+
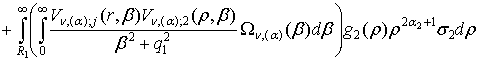 +
+
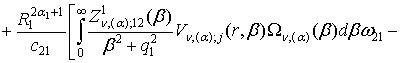
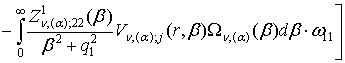 +
+
+
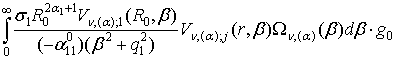 , j = 1, 2. (20)
, j = 1, 2. (20)
Порівнюючи розв’язки (12) та (20) в силу єдиності,
одержуємо наступні формули обчислення
поліпараметричних невласних інтегралів [5]:
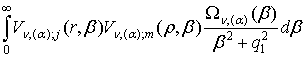 =
=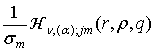 ; j, m = 1, 2, (21)
; j, m = 1, 2, (21)
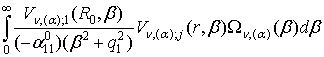 =
=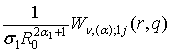 ; j = 1, 2, (22)
; j = 1, 2, (22)
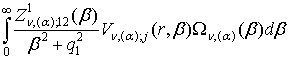 =
=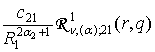 ; j = 1, 2, (23)
; j = 1, 2, (23)
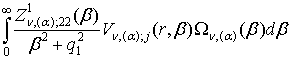 =
=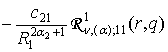 ; j = 1, 2, (24)
; j = 1, 2, (24)
У
рівностях (21) – (24) функції Hn, (a); jm(r, r, q) визначені формулами
(9), функції Wn, (a); 1j(r, q) – формулами (10), а функції Гріна ![]() – формулами (11).
– формулами (11).
Зауважимо, що при max{![]() ;
; ![]() } =
} = ![]() > 0
> 0 ![]() ,
, ![]() = 0. У цьому випадку замість
= 0. У цьому випадку замість ![]() стоятиме
стоятиме ![]() .
.
Оскільки
праві частини формул (21) – (24) не залежать від нерівностей ![]() ³ 0 (у випадку max{
³ 0 (у випадку max{![]() ;
; ![]() }
=
}
= ![]() ) або
) або ![]() ³ 0 (у випадку max{
³ 0 (у випадку max{![]() ;
; ![]() } =
} = ![]() ),
то можна покласти
),
то можна покласти ![]() , звужуючи при цьому сім’ю невласних поліпараметричних інтегралів.
, звужуючи при цьому сім’ю невласних поліпараметричних інтегралів.
Підсумком
викладеного вище є твердження.
Теорема. Якщо вектор-функція f(r) = {![]() } неперервна на множин
} неперервна на множин ![]() , функції gj задовольняють крайові
умови (2) та умови спряження (3) й
виконується умова (8) однозначної розв’язності крайової задачі (1) – (3), то
справджуються формули обчислення невласних поліпараметричних інтегралів за
власними елементами ГДО
, функції gj задовольняють крайові
умови (2) та умови спряження (3) й
виконується умова (8) однозначної розв’язності крайової задачі (1) – (3), то
справджуються формули обчислення невласних поліпараметричних інтегралів за
власними елементами ГДО ![]() , визначеного рівністю
(13).
, визначеного рівністю
(13).
1.
Степанов В.В. Курс
дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.
2.
Ленюк М.П. Исследование основных
краевых задач для диссипативного волнового уравнения Бесселя. – Киев, 1982. –
62 с. – (Препринт / АН УССР. Ин-т математики; 83.3).
3.
Шилов Г.Е. Математический анализ. Второй специальный курс. – М.: Наука,
1965. – 328 с.
4.
Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є,
Бесселя, Лежандра). Частина 1. – Тернопіль: Економічна
думка, 2004. – 368 с.
5.
Ленюк М.П. Обчислення невласних інтегралів методом гібридних інтегральних
перетворень (Фур’є, Бесселя, Лежандра). Том V. – Чернівці: Прут, 2005. – 368
с.