Математика/ Математическое моделирование
Академик РАН
А.М. Липанов, аспирант А.Н. Семакин
Институт
прикладной механики УрО РАН
Применение метода конечных объёмов
к задаче обтекания сферы
1. На данный момент процесс обтекания
сферы потоком вязкой жидкости или газа достаточно хорошо изучен, имеется
значительное количество экспериментальных данных [1-4]. Поэтому задачу
обтекания сферы можно рассматривать в качестве тестовой для апробации различных
новых численных методик решения задач механики жидкости и газа. В [5] предложен
достаточно простой с точки зрения реализации метод исследования течения жидкости
или газа в многосвязных областях путём деления исследуемой области на определённое
число подобластей (конечных объёмов, КО) более простой структуры, в каждом из
которых вводится собственная система координат и формулируется система
уравнений гидромеханики. Для проверки работоспособности его теоретических
положений использовалась задача обтекания сферы вязким газом.
2. Расчётная область представляет собой
шар радиуса 7.8, в который помещена сфера радиуса 0.5. Расстояние от сферы до
внешней границы составляет 14 радиусов. Согласно [5] данная расчётная область
делится на 6 конечных объёмов. На рис. 1 приведено данное деление в
вертикальной плоскости симметрии. В каждом таком КО вводится собственные
локальные декартовая ![]() и криволинейная
и криволинейная ![]() системы координат,
связанные соотношениями:
системы координат,
связанные соотношениями:
![]() ,
, ![]() ,
, ![]() , где
, где ![]() ,
, ![]() .
.
В данной локальной системе координат
формулируется система уравнений гидромеханики в безразмерной форме, включающая
уравнение неразрывности, три уравнения импульса и уравнение энергии. При её
интегрировании по времени использовался метод Рунге-Кутта второго порядка
точности, при аппроксимации пространственных производных применялась
центральная разностная схема произвольного порядка точности. После проведения
очередного шага по времени из одного КО в другой передаются необходимые для
дальнейших расчётов значения гидромеханических параметров (скорость, плотность
и температура) с помощью интерполяции отрезком ряда Фурье по ортогональным многочленам
степени не выше второй.
Число Маха ![]() бралось 0.1. В этом
случае результаты расчётов должны приблизительно совпадать с данными для
несжимаемой жидкости и, следовательно, значения
бралось 0.1. В этом
случае результаты расчётов должны приблизительно совпадать с данными для
несжимаемой жидкости и, следовательно, значения ![]() , полученные путём расчётов, можно сравнивать со стандартной
кривой коэффициента сопротивления сферы несжимаемой жидкости, аппроксимируемой
зависимостью [1, 2]:
, полученные путём расчётов, можно сравнивать со стандартной
кривой коэффициента сопротивления сферы несжимаемой жидкости, аппроксимируемой
зависимостью [1, 2]:
![]() ,
, ![]() .
.
3. В табл. 1 представлена сходимость
коэффициента сопротивления сферы в зависимости от количества точек и порядка
точности разностной схемы по пространственным переменным при ![]() . В первой колонке указывается используемая разностная сетка,
причём первая цифра 6 означает, что данная сетка применяется в каждом из шести
КО. Из табл. 1 видно, что при расчёте по разностной схеме с шестым порядком
точности значение
. В первой колонке указывается используемая разностная сетка,
причём первая цифра 6 означает, что данная сетка применяется в каждом из шести
КО. Из табл. 1 видно, что при расчёте по разностной схеме с шестым порядком
точности значение ![]() , полученное на самой грубой сетке при дальнейшем увеличении
точек практически не меняется, т.е. для определения коэффициента сопротивления
сферы при расчётах с шестым порядком достаточно использовать самую грубую разностную
сетку.
, полученное на самой грубой сетке при дальнейшем увеличении
точек практически не меняется, т.е. для определения коэффициента сопротивления
сферы при расчётах с шестым порядком достаточно использовать самую грубую разностную
сетку.
В табл. 2 приведены результаты расчётов ![]() при различных числах
Рейнольдса на сетке 6
при различных числах
Рейнольдса на сетке 6![]() 30
30![]() 13
13![]() 13 по схеме шестого порядка точности. В табл. 2
13 по схеме шестого порядка точности. В табл. 2 ![]() - значение коэффициента
сопротивления, полученного в ходе расчётов,
- значение коэффициента
сопротивления, полученного в ходе расчётов, ![]() - значение,
полученное по аппроксимационной зависимости. Из данной таблицы видно, что
значения
- значение,
полученное по аппроксимационной зависимости. Из данной таблицы видно, что
значения ![]() , полученные в ходе расчётов, хорошо соответствуют
стандартной кривой коэффициента сопротивления.
, полученные в ходе расчётов, хорошо соответствуют
стандартной кривой коэффициента сопротивления.
Также при числах Рейнольдса 50, 100 и 250
были измерены длина отрывной зоны за сферой и угол отрыва потока. Длина
отрывной зоны составила 0.4, 0.8, 1.1, а угол отрыва - 41![]() , 52
, 52![]() , 65
, 65![]() , соответственно. Эти результаты полностью согласуются с
данными, приведёнными в [1,4], но занижены по сравнению с [2].
, соответственно. Эти результаты полностью согласуются с
данными, приведёнными в [1,4], но занижены по сравнению с [2].
На рис. 2 представлено поле скоростей за
сферой при ![]() и
и ![]() . На рис. 3 приведены линии тока в этой же области для тех же
чисел Рейнольдса. При проведении расчётов были получены следующие результаты. Когда
число Рейнольдса
. На рис. 3 приведены линии тока в этой же области для тех же
чисел Рейнольдса. При проведении расчётов были получены следующие результаты. Когда
число Рейнольдса ![]() не превышало 300, за
сферой получалось стационарное вихревое кольцо с осью симметрии
не превышало 300, за
сферой получалось стационарное вихревое кольцо с осью симметрии ![]() , размеры которого росли с ростом
, размеры которого росли с ростом ![]() . Начиная примерно с
. Начиная примерно с ![]() , течение за сферой становится нестационарным и носит
периодический характер изменений. Если рассматривать этот процесс в плоскости
, течение за сферой становится нестационарным и носит
периодический характер изменений. Если рассматривать этот процесс в плоскости ![]() , то получается следующее. В нижней части области за кормой
сферы на некотором удалении от неё возникает вихрь значительного размера. Этот
вихрь с течением времени приближается к поверхности сферы, одновременно
уменьшаясь в размере и смещаясь вверх. Через некоторый промежуток времени он
исчезает. В верхней части кормового пространства за сферой также генерируется
вихрь, но в отличие от нижнего вихря его размеры малы. Далее этот вихрь
увеличивается в размере и отрывается от сферы.
Указанный процесс для обоих вихрей повторяется периодически.
, то получается следующее. В нижней части области за кормой
сферы на некотором удалении от неё возникает вихрь значительного размера. Этот
вихрь с течением времени приближается к поверхности сферы, одновременно
уменьшаясь в размере и смещаясь вверх. Через некоторый промежуток времени он
исчезает. В верхней части кормового пространства за сферой также генерируется
вихрь, но в отличие от нижнего вихря его размеры малы. Далее этот вихрь
увеличивается в размере и отрывается от сферы.
Указанный процесс для обоих вихрей повторяется периодически.
4. Основной вывод работы – метод конечных
объёмов даёт правильные результаты, соответствующие данным, полученным другими
методами, и может быть использован при моделировании течения вязкого газа.
Список
литературы:
1.
Горохов
М.М. Математическое моделирование обтекания и горения гранул твёрдого топлива в
турбулентных потоках: Дис… д-ра физ.-матем. наук. – Ижевск, 2005.
– 258 с.
2.
Двухфазные
моно- и полидисперсные течения газа с частицами / Под ред. Л.Е. Стернина.
– М.: Машиностроение, 1980. – 184 с.
3.
Шлихтинг
Г. Теория пограничного слоя. – М.: Наука, 1974. – 712 с.
4.
Гущин В. А.,
Матюшин П. В. Численное моделирование пространственных отрывных
течений // Применение математического
моделирования для решения задач в науке и технике: Сб. трудов конференции (Ижевск, 1996). – Ижевск: ИПМ УрО РАН, 1996. – с. 44–61.
5.
Липанов А.М. Метод
численного решения уравнений гидромеханики в многосвязных областях
//Математическое моделирование. – 2006. - т.18. - № 12. - с. 3-18.
Таблица 1
Сходимость коэффициента
сопротивления сферы
|
|
2 |
4 |
6 |
|
6 |
1.502 |
1.130 |
1.099 |
|
6 |
1.320 |
1.114 |
1.098 |
|
6 |
1.246 |
1.096 |
1.092 |
Таблица 2
Коэффициент сопротивления
сферы
|
|
|
|
|
50 |
1.582 |
1.609 |
|
100 |
1.099 |
1.121 |
|
250 |
0.723 |
0.756 |
|
500 |
0.601 |
0.597 |
|
1000 |
0.536 |
0.495 |
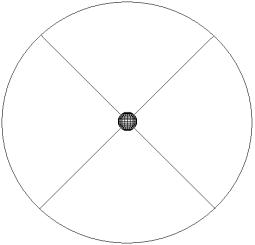
Рис. 1. Разбиение расчётной области на КО в плоскости ![]()
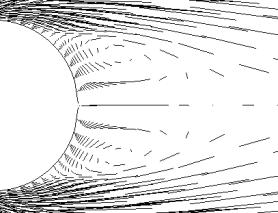
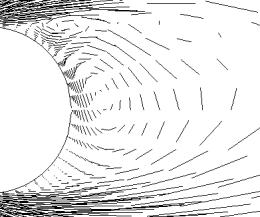
а) б)
Рис. 2. Поле скоростей за сферой в плоскости ![]()
а) ![]() , б)
, б) ![]()
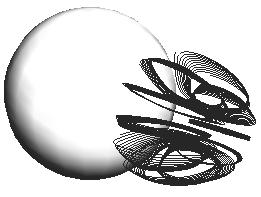

а) б)
Рис. 3. Линии тока за сферой при а) ![]() , б)
, б) ![]()