УДК 532.685
М. Р. Кулиманова, Б. С. Кабатаева
Казахский
национальный университет имени аль-Фараби
О МЕТОДЕ РЕШЕНИЯ ОДНОЙ ЗАДАЧИ ТЕОРИИ ФИЛЬТРАЦИИ
СО СВОБОДНЫМИ
ГРАНИЦАМИ
В данной работе исследована двумерная задача теории
фильтрации со свободными границами. Предлагаемый метод применен ранее в работе [1] с целью построения класса
точных решений двумерных задач неоднородной жидкости и магнитной гидродинамики.
В случае определения топологической структуры течения недостаточно ограничиться
стационарной моделью. Развивается указанный в работе [1] метод для систем уравнений теории фильтрации
составного типа. Известно [2-4], что в случае фильтрации двухфазной жидкости в пористой среде,
движение фаз подчиняется обобщенному закону Дарси и насыщенности 
смачивающей жидкостью, причем
уравнение относительно насыщенности вырождается на искомом решении.
Постановка
задачи. Будем рассматривать
двухкомпонентную жидкость, как совокупность континуумов, заполняющих один и тот
же объем несжимаемого парового пространства. Для каждого из континуумов, помимо
насыщенностей 
, введем свою плотность
, скорость фильтрации
и давление 
. Тогда уравнения неразрывности каждой компоненты жидкости
могут быть записаны в виде
(1)
Учитывая качественную картину многофазной фильтрации, М.Маскет
предложил следующее формальное обобщение закона Дарси для каждой из жидкостей:
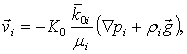
(2)
где 
- по-прежнему коэффициент фильтрации пористой среды для
однородной жидкости (или симметричный тензор для анизотропной среды), 
- коэффициенты
динамической вязкости, а 
- относительные
фазовые проницаемости. При этом 
должны зависеть от
насыщенности 
, поскольку часть парового пространства занята другой
жидкостью. По определению насыщенности 
меняются в пределах 
и по достижении значений 
движение 
-й компоненты прекращается, что обеспечивается выполнением
условий 
Ниже рассматривается
плоское установившееся течение несмешивающиеся двухфазной жидкости в пористой
среде в области 
, имеющий вид
плоского канала 
с одной криволинейной
стенкой 
. Для определенности будем считать, что жидкость втекает в 
через участок 
и вытекает через 
. Боковые стенки 
и 
считаем
непроницаемыми для жидкости. Пусть 
- длина канала, 
– ширина входа
канала, т.е. длина отрезка 
; 
- уравнение границы 
. Такое движение жидкости в пористой среде соответствует
вытесняющему агенту от нагнетательной скважины до добывающей скважине.
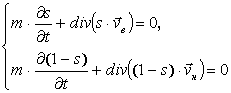(3)
При указанных выше предположениях уравнение (3)
преобразуется следующему виду:
(4)
где 
- приведенная скорость. С другой стороны, из (2) и (4) без
учета гравитационных и учетом капиллярных сил имеем:
(5)
или 
.
Тогда из последнего
уравнения путем перекрестного дифференцирования получим следующее уравнение:
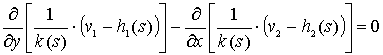. (6)
Исходя из результатов
работы [3] считаем,
что 
Тогда, исходя из результатов работы [2] с помощью
замены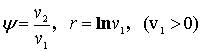 
преобразуем (6)
следующим образом:
(7)
где 
- относительная проницаемость.
В силу
условий непроницаемости функция 
на 
и 
, а функция s на 
удовлетворяют условиям:
(8)
В
случае нестационарной задачи для замыкания математической модели добавляется
следующее начальное условие:
, причем 
при 
. (8’)
На границе 
будем считать
значение r известным, т.к. на
нагнетательной скважине задается расход. Для определения единственного решения
системы (5) необходимо еще задать значения 
на 
и 
. Указанные значения 
не задается, а
определяется из условия существования точного решения системы (7). С учетом
краевых условий (8) можно положить 
где 
- некоторая функция,
определенная на промежутке [0, 1], удовлетворяющая условиям 
и 
- является
неизвестной функцией. Таким образом, задача сведена к решению уравнений (5),
причем в области течения фильтрационного канала выполняется условие:
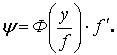(9)
Применяя метод
характеристик во второе уравнение из (7) легко получить явный вид функций:
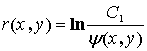
(10)
Домножение первого
уравнения на функцию 
и сложив со вторым уравнением из систем уравнений (7) получим:
. (11)
С другой
стороны, со второго уравнения из (7): 
. Подставляя последнее соотношение в (11) имеем 
, либо с учетом (10) получим:
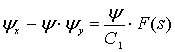(12)
Далее,
применяя метод характеристик относительно уравнения (12) в явном виде
относительно функции 
получим следующее интегральное выражение:
,
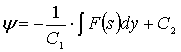либо из представления из
функций 
имеем:
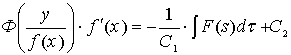. (13)
Для определения
постоянных воспользуемся условиями относительно функций 
, т.е. при 
имеем 
, а при 
получим
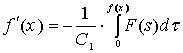(14)
С помощью (14) и с
учетом 
составим следующее
рекуррентное соотношение:
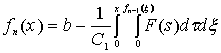, (15)
где 
. Найденные значения
постоянных, окончательно позволяют получить представление относительно функций 
:
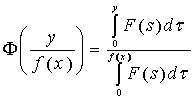(16)
Полученные
соотношения в (14) – (16) позволяют определить полностью искомые функции и
окончательный результат можно сформулировать в виде следующей теоремы.
Теорема. При выполнении
условий 
>1 , (8) и (8’) для решения рассматриваемой задачи справедливы
представления (15), (16) и для насыщенности имеет место:
.
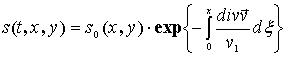Литература
1.
Алексеев Г.В., Мокин
Ю.А. Класс точных решений двумерных
уравнений гидродинамики и магнитной гидродинамики идеальной жидкости. –В сб.:
Динамика сплошной среды. –Новосибирск, 1972, вып. 12, с.5-13.
2.
Levitt L.C.
Some Exact Solutions for a Class of two-dimensional Gydromagnetic steady Flows.
J. Math. Analysis and Appl. 1963, 6, p.483-396.
3.
Антонцев С.Н., Монахов
В.Н. О некоторых задачах фильтрации двухфазной несжимаемой жидкости. –В сб.:
Динамика сплошной среды. –Новосибирск, 1969, вып. 2, с.156-167.
ABOUT THE METHOD
OF THE DECISION OF ONE PROBLEM OF THE THEORY OF THE FILTRATION
Summary. In work the class of exact decisions of a problem of a biphase
filtration of a liquid in the porous environment is considered. In a
two-dimentional case the algorithm of construction of the decision of the
considered problem containing free (unknown) border is resulted.