БІР АРНАЙЫ ТҮРДЕГІ КЕЗДЕЙСОҚ ПАРАБОЛАЛЫҚ ТЕҢДЕУДІ ОРТАЛАНДЫРУ

Х.А.Аширбаев, Ж.А.Тлесбаева, А.И.Джумагалиева, Д.А.Жүнісбекова, С.Р.Дулатов

(Шымкент қ., М.Әуезов атындағы ОҚМУ)

Айталық, қандай да бір ықтималдық кеңістігі, осы ықтималдық кеңістігінде анықталған кездейсоқ функциялар Щ , кездейсоқ емес функция болсын. Мынадай арнайы түрдегі кездейсоқ параболалық теңдеуді қарастыралық:

Бұл жұмыстағы біздің мақсатымыз - (1) теңдеуді орталандыру, яғни (бұл жерде және бұдан былай қарай бұрыштық жақша ықтималдықтық өлшемі бойынша орталандыруды (математикалық күтім алуды) білдіреді) орталандырылған функциясы үшін теңдеу алу.

Айталық, берілген ықтималдық кеңістігінде анықталған Винер процесі болсын, ал арқылы осы Винер процесінің бастапқы уақыт сәтінде нүктесінен шығатын барлық траекториялары бойынша шартты математикалық күтім алуды ( яғни, ), ал барлық оқиғаларын қамтитын (мұндағы сан түзуіндегі борелдік алгебра) ең кіші алгебраны арқылы, , деп белгілелік.

Төменде біз кездейсоқ функцияларының траекториялары бойынша шенелген және үзіліссіз, сонымен бірге функциялары шенелген және үзіліссіз болсын деп есептейміз (айта кетелік, бұл жұмыста біз кездейсоқ функциялардан алынған туындыларды және интегралдарды үнемі сәйкес орташа квадраттық мағынадағы туынды және интеграл ретінде түсінетін боламыз).

(1)-теңдеудің коэффиценттеріне және бастапқы функцияға байланысты жоғарыда келтірілген шарттар орындалған жағдайда (1)-теңдеудің шешімін келесі

шартты математикалық күтімі түрінде жазуға болатынын көрсету қиын емес (жоғарыда айтып кеткеніміздей, (2)-формуладағы экпоненталардың дәрежелерінде тұрған стохастикалық интегралдарды сәйкес интегралдық қосындылардың орташа квадраттық мағынадағы шектері деп түсінеміз және функциясынан алынған интеграл Винер процесі бойынша алынған Ито интегралы екенін еске саламыз).

Шындығында да (2)-формуладан

шығатыны айқын. Ары қарай деп алып, процесінің марковтық қасиетін, процесі дан тәуелсіздігін, өлшенетіндігін және шартты математикалық күтім мен стохастикалық интегралдардың қасеттерін пайдаланып

қатынасы дұрыс болатынын көреміз.

Ары қарай (4) - формуладағы экспонентаны және функциясын екінші аргументі бойынша нүктесінің маңайында -ға дейінгі дәлдікпен жіктеп, ең соңында үшін алынған қатынастың екі жағын да - ға бөліп және шегіне көшіп, үшін (1)-теңдеудің дұрыстығын көреміз.

Енді орталандырылған функциясы үшін теңдеу алу туралы сұраққа көшелік. Ескертіп айта кетелік, бұл жағдайда (1)-теңдеудің екі жағынан бірдей математикалық күтімдер алып, кездейсоқ функцияларды олардың математикалық күтімдерімен ауыстыруға болмайды, себебі тәуелді кездейсоқ функциялар үшін көбейтіндінің математикалық күтімі математикалық күтімдердің көбейтіндісіне тең болуы міндетті емес - бізде болмауы мүмкін, өйткені функциясы ке тәуелді ( арқылы өрнектеледі) т.с.с.

(3)-қатынастың оң жағын – ға дейінгі дәлдікпен жіктеп (мұнда функциясын екінші аргументі бойынша нүктесінің маңайында жіктейміз), сосын орталандыруына көшіп, мынаны аламыз:

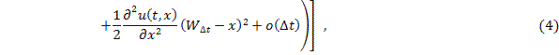
мұндағы

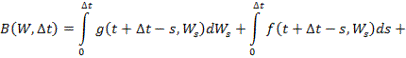
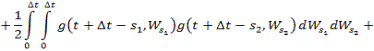
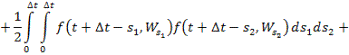
(5)

Алынған өрнектерді (4) - теңдеуге қойып, сосын ті (4) - тің сол жағына шығарып, ақыр соңында алынған қатынастың екі жағын да ға бөліп, шегіне көшу арқылы (1) - теңдеудің орталандырылған шешімі үшін дәл осы теңдеудің өзіне ұқсас (бірақ коэффиценттері кездейсоқ емес функциялар болатын) келесі теңдеуді аламыз:

(6)

Егер те кездейсоқ, бірақ процесінен тәуелсіз функция болса, онда соңғы теңдеудегі бастапқы шарт шартына ауысатынын байқау қиын емес. Сонымен бірге (6) - теңдеудің шешімі үшін (2) - формуланың дұрыс болатынын (тек мұнда функцияларын сәйкес функцияларына ауыстыру керек) да айта кетелік.

Ары қарай (6) - теңдеудің ( кездейсоқ емес ) коэффиценттері тек тің ғана функциясы болсын деп ұйғарсақ, онда бұл теңдеудің шешімі үшін

(7)

формуласы дұрыс болады (бұл жерде және бұдан былай қарай біз функциялардың төбелеріндегі сызықшаларды жазбаймыз ).

(7) - формула , функционалдарының бірлескен сипаттамалық функциясын табуға мүмкіндік береді.

Егер жеке жағдайды, функционалын қарастырсақ, онда

(7) - формуладан бұл функционалдың шартты сипаттамалық функциясы

теңдеуін қанағаттандыратынын аламыз. Онда ның сипаттамалық функциясы функциясы болады.

Пайдаланылған әдебиеттер

1. А.Д.Вентцель. Курс теории случайных процессов-М.: Наука,1985

2. А.Н.Ширяев, А.В.Булинский. Теория случайных процессов – М.: Физматлит., 2005.
3.А.В.Скороход, Н.П.Слободенюк. Предельные теоремы для случайных блужданий – Киев.: Наукова думка, 1970.