Engineering / 12. Automated control systems in manufacturing
Ladieva L. R., Dubyk N. Ì.
National Technical
University of Ukraine “Kyiv Polytechnic Institute”
OPTIMAL
CONTROL PROCESS OF RECTIFICATION
Consider the way automated process control
rectification of ethylene oxide in the distillation column, which involves
measuring the temperature in the control plate and adjustment expenses mixture
of ethylene at the inlet of the distillation column, characterized in that the
supply mix at the inlet and the concentration at the outlet of the column
adjusting via Smith’s advance.
With the advent of digital technology to realize the time delay was easy
enough that simplify the implementation of Smith’s advance. However, the widespread use limits the
number of shortcomings. First, this lack of engineering methods settings of the
SAR with Smith’s advance.
Secondly, the SAR with Smith’s
advance are very sensitive to changes in the parameters of the object in the
process (by changing the parameters of the object without adjusting the
parameters of SAR with Smith’s
advance significantly worse quality of the transition process and increases the
likelihood of loss of system stability). These shortcomings are also
characteristic and modifications of Smith’s advance[*].
In order to eliminate the above drawbacks of using Smith’s advance and his modifications were carried out
research on the algorithm of optimal parametric synthesis (OPS) for regulation
parameters of SAR with Smith’s
advance and Smith’s advance
modified PPI-D-regulator (the "Predictive PI"). Details are described
below.
The problem of optimal parametric synthesis for the SAR process of
rectification to the above regulators follows.
The criterion of
optimization:
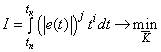, (1)
where tn, tk
– limits of integration; (|e(t)jti|) – objective
function; e(t ) – unbalance signal; t – time; i, j– constant integer coefficients; i=0,1,2…; j=1,2; 
– SAR parameter vector
to be optimization.
Restrictions on the control signal:
. (2)
where u(t ) – control signal
at the output of the regulator.
The transfer function of the
cube distillation column:
Wob(s) =
, (3)
where 
– gain of the object; 
– the time constant of the object; τob – delay of the object.
For Smith’s advance:
- transfer function of PI -
regulator:
Wp(s) =
), (4)
where Êð – gain of the PI-regulator; Ò³ – integration constant of the PI- regulator;
- modular transfer function
block:
Wm (s) =
(5)
where Êm – gain model of the object; Òm – time
constant of the object model; τm – late of the model object.
For modified Smith’s advance, broadcasting function
of the P²-controller that broadcasting function of the model blocks are the
same, a broadcasting function of the dynamic compensator has the form:
M(s) = 
, (6)
äå À1, À0, Â1,– dynamic equalizer coefficients.
The transfer
function of PI-regulator:
WPPI (s) =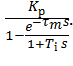
(7)
The results of the SAR. The best results were obtained OPS in case of simultaneous optimization
of parameters of PI-regulator and object model for Smith’s advance and modified Smith’s advance. Calculations were conducted to optimize
every step to reduce the impact of dynamic compensator on its results. In the
case of PPI- regulator best results were also obtained with simultaneous
optimization of its parameters Êð, Ò³
òà
τm.
Research conducted by the example
object described transfer function (8). This transfer function describes the
flow channel mixture of ethylene – the concentration of ethylene oxide at the
outlet of the distillation column.
(8)
Optimal parametric synthesis of automatic control with Smith’s advance and modified Smith’s advance and PPI-held controller ideal for
both when the values coincide with the initial object, and for which the ASR
conducted preset, and for when values about the object was changed to 50%
compared with the original.
The initial PS parameters
controller used in our SAR with Smith’s advance determined
using simplified formulas for calculating the process with a minimum area of
quadratic deviation.
Ò³
= Òob . (9)
Initial
settings object model to be chosen as close to the parameters of the object,
that is, in the ideal case. For SAR of PPI-regulator initial values Êð òà Ò³
are
calculated as for the PI-regulator in Smith’s advance, and the value object model delay τì elected as close to the value of the control object delay τ.