Трубачев С.І., Колодежний В.А.

Національний технічний університет України «Київський політехнічний інститут»

ЧИСЕЛЬНЕ МОДЕЛЮВАННЯ ТРИШАРОВИХ ПЛАСТИН

Пружна тришарова пластина з жорстким заповнювачем знаходиться на пружній основі. Для опису кінематики пакету прийняті гіпотези ламаної лінії: в несучих шарах справедливі гіпотези Кірхгофа, в нестисливому по товщині заповнювачі нормаль залишається прямолінійною, не змінює своєї довжини, але повертається на деякий додатковий кут, що становить з координатними осями величини , . Деформації вважаємо малими. На пластину діють зовнішні розподілені поверхневі навантаження , , і реакція основи. Реакція основи відповідає моделі Вінклера

, (1)

де – коефіцієнт жорсткості основи, – прогин пластини; знак мінус вказує на те, що реакція спрямована в бік, протилежний прогину

Система координат x, y, z зв'язується з серединною площиною заповнювача. Через , , позначені прогин і осьові поздовжні переміщення серединної поверхні заповнювача. На контурі пластини передбачається наявність жорсткої діафрагми, що перешкоджає відносному зсуву шарів. Позначимо через товщину -го шару, при цьому (k = 1, 2, 3).

Використовуючи введені геометричні гіпотези, поздовжні переміщення в шарах можна виразити через шукані п'ять функції :

, ,

, , (2)

, ,

де – відстань від розглянутого волокна до серединної площини заповнювача, – величина зміщення зовнішнього несучого шару за рахунок деформації заповнювача, для другого несучого шару це зміщення буде відповідно .

Компоненти тензора деформацій виражаються через п'ять шуканих функцій за допомогою співвідношень Коші і виразів (2):

,

,

,

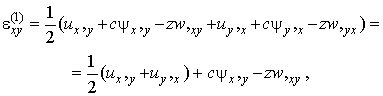
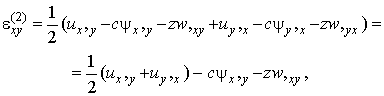(3)

,

.

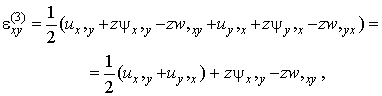Шарова і девіаторна частини тензора деформацій в розглянутому випадку будуть наступними

. (4)

Введемо внутрішні зусилля і моменти наступними співвідношеннями:

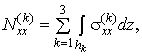
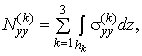
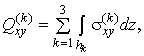(5)

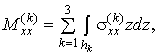
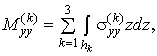
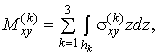
де , , , – компоненти тензора напружень в шарах пластини, інтеграли беруться за товщиною -го шару.

Рівняння рівноваги знаходимо з принципу можливих переміщень:

. (6)

Тут варіація роботи зовнішніх поверхневих сил:

. (7)

Варіація роботи внутрішніх сил враховує роботу заповнювача в тангенціальному напрямку:

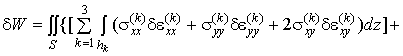
. (8)

Варіації переміщень у шарах:

, ,

, , (9)

, .

Підставивши вирази для інтегралів по товщині шарів у формулу (8), і прирівняти нулю, коефіцієнти при незалежних варіаціях, отримаємо систему диференціальних рівнянь рівноваги прямокутної тришарової пластини на пружній основі в зусиллях:

, , ,

, . (10)

Для зв'язку напружень і деформацій в шарах використовуємо співвідношення закону Гука в девіаторно-кульовій формі:

, (11)

де – модулі зсуву та об'ємної деформації, , – девіаторна і кульова частини тензора напружень, – девіаторна і кульова частини тензора деформацій.

Компоненти тензора напружень у шарах з урахуванням виразів (5) та (11) будуть:

(12)

де

Підставляючи у (8) вираження деформацій через шукані переміщення (3), та використовуючи інтегрування по товщині кожного з шарів, і враховуючи вирази (7), (6) і (1) отримаємо з (10) систему п'яти лінійних диференціальних рівнянь рівноваги щодо шуканих переміщень:

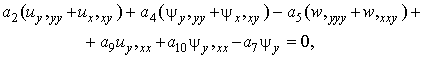(13)

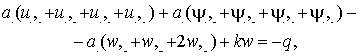
де ,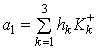 

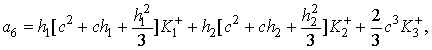
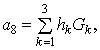
Приймаються граничні умови, що відповідають вільному опиранню пластини по кромках. Тоді для шуканих переміщень повинні виконуватися при наступні вимоги [1]:

. (14)

Для відповідності умов (14) рішення системи диференціальних рівнянь (13) приймається у вигляді розкладання в подвійні тригонометричні ряд [2,3]:

, ,

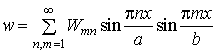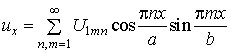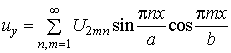, (15)

,

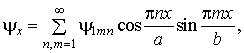
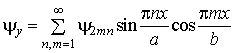де – невідомі амплітуди переміщень.

Нехай поздовжнє навантаження . Поперечне навантаження представимо у вигляді розкладання в подвійний тригонометричний ряд:

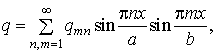
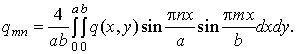(16)

Після підстановки переміщень (15) і навантаження (16) в рівняння (13) отримаємо систему лінійних алгебраїчних рівнянь для визначення шуканих амплітуд переміщень:

(17)

де коефіцієнти виражаються через величини і залежать від параметрів m і n.

Рішення системи (17) можна отримати чисельно за допомогою оберненої матриці. Після визначення амплітуд шукані функції обчислюються за формулами (15).

Переміщення в несучих шарах і заповнювачі знаходяться з співвідношень (2).

Розрахунок здійснювався для тришарової пластини, матеріал несучих шарів якої Д16Т, а для заповнювача – фторопласт. Відносні товщини шарів приймалися , , , співвідношення сторін пластини – . Розрахунки проводилися двома способами: за розглянутою вище методикою та методом скінченних елементів (МСЕ). Максимальна похибка не перевищувала 2,8 %.

Список використаної літератури

1. Горшков, А. Г. Механика слоистых вязко-упругопластических элементов конструкций / А. Г. Горшков, Э. И. Старовойтов, А. В. Яровая. – М. : Физматлит, 2005.– 576 с.

2. Старовойтов, Э. И. Вязкоупругопластические слоистые пластины и оболочки / Э. И. Старовойтов. – Гомель : БелГУТ, 2002. – 344 с.

3. Старовойтов Э.И. Деформирование трехслойных элементов конструкций на упругом основании / Э.И. Старовойтов, А.В. Яровая, Д.В. Леоненко.-М.:ФИЗМАТЛИТ, 2006. – 379 с.

4. Плескачевский, Ю. М. Деформирование металлополимерных систем [Текст] / Ю. М. Плескачевский, Э. И. Старовойтов, А. В. Яровая. – Минск : Бел. Навука, 2004. – 386 с.