УДК 66.074
Дуанбекова А.Е., Есимов Е.К., Култасов
Б.Ш.
Южно-Казахстанский
Государственный Университет им.М.Ауезова
Республика Казахстан
моделирование
переноса активной примеси в
неоднородных пористых адсорбентах
Анализ процессов переноса примесей загрязняющих веществ в жидких средах, движущихся через неоднородные пористые среды, имеет большое значение для инженерных химико-технологических и экологических расчетов. Несмотря на довольно большое количество работ, посвященных отмеченным проблемам, некоторые существенные аспекты остаются слабо разработанными.
В частности, это касается учета особенностей движения примеси в неоднородных средах в условиях ее адсорбции на поверхности пор среды и последующей внутренней диффузии и возможных химических реакций в потоке. Нужно отметить также большой диапазон характерных пространственных размеров решаемых задач. При описании распространения примесей с грунтовыми водами характерные горизонтальные размеры задачи могут составлять несколько километров, тогда как вертикальный размер порядка сотни метров. Пористость среды и ее адсорбционные характеристики на таких расстояниях могут существенно изменяться.
При решении задач процессов и аппаратов химических технологий характерные размеры значительно меньше. Однако в этих задачах важен учет химического взаимодействия, а неоднородность может быть обусловлена неравномерной укладкой адсорбента или особенностями конструкции аппарата.
В настоящей работе изложена математическая модель, учитывающая отмеченные аспекты проблемы и предлагающая методы решения соответствующих инженерных задач.
Рассмотрим пористую среду, в которой осуществляется
фильтрационное движение жидкости с некоторой активной примесью. Предполагается
возможная пространственная неоднородность среды, которая моделируется переменной
пористостью 
. Однако эффектами временной эволюции пористости пренебрегаем.
Это означает, что отсутствует деформация среды, а также поры не забиваются
твердыми осадками.
Тогда баланс массы для примеси можно записать
следующим образом:
,
(1)
где
- концентрация примеси в жидкой фазе;
- конвективно-диффузионный поток примеси в жидкой фазе;
- поток примеси, обусловленный адсорбцией в порах среды;
- источник (или сток) примеси, обусловленный химическими
реакциями;
- время.
Конвективно-диффузионный поток определяется выражением:
, (2)
где
- средняя скорость жидкой фазы в исследуемом сечении;
- коэффициент диффузии.
Для потока примеси, обусловленного адсорбцией, соответствующее выражение получим, исходя из принципа локального термодинамического равновесия на поверхности пор адсорбента и быстрой внутренней диффузии. Тогда можно записать:
, (3)
,
(4)
где
- концентрация примеси в адсорбенте;
- коэффициент термодинамического равновесия.
Для реакции первого
порядка, протекающей в потоке фильтрующей жидкости, получим:
, (5)
где
- константа скорости
реакции.
Вводя
фактор задержки [1,2]:
, (6)
перепишем
(5) в виде:
. (7)
Если превалирующее значение в описании имеет продольный характерный размер 
, уравнение (7) преобразуется к виду:
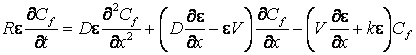. (8)
В
однородной пористой среде уравнение (8) упрощается: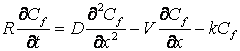 
.
(9)
Коэффициент диффузии в
пористой среде при строгом описании отличается от молекулярного коэффициента
диффузии и может быть представлен в виде 2]:
, (10)
где
- собственно молекулярный коэффициент диффузии;
- символ Кронекера (
);
- компоненты тензора дисперсности пористой среды;
- компоненты вектора
скорости жидкости по направлениям осей координат;
- амплитуда скорости жидкости, определяемая обычно по формуле
[1]: 
. (11)
Для изотропной среды компоненты тензора дисперсности определяются по формуле [1,2]:
,
(12)
где два параметра 
характеризуют
поперечную и продольную дисперсности среды.
Отсюда получаем:
.
(13)
В итоге выражение для потока примеси
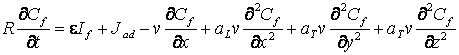. (14)
1- начальный момент времени; 2-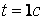 
; 3- 
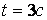; 4-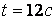 
Рис. 1 Характерные графики рассеивания примеси с учетом адсорбции в пористой среде.
Для примеси, локализованной в начальный момент в окрестности начала координат, получаем приближенно-аналитическое решение в виде, аналогичном [2]:
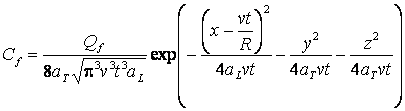, (15)
где 
- общая начальная масса примеси в жидкости.
На рисунке 1 приведены некоторые графики, иллюстрирующие процесс рассеивания примеси, рассчитанный по приведенным соотношениям.
ЛИТЕРАТУРА.
1. А. Verruijt.
The Mathematics of Transport Phenomena in Heterogeneous porous Media //
ACOMEIV, 1998, P. 89-100.