Ющенко О.А., Кусайнов Р.Р.

Карагандинский государственный индустриальный университет,

Казахстан

Исследование работы нечеткого ПИД-регулятора

В настоящее время в промышленности, несмотря на большое количество разработок в области адаптивного и оптимального регулирования, управление технологическими процессами в подавляющем большинстве случаев осуществляется с помощью ПИД-регуляторов. Однако системы управления, построенные на таких принципах, являются детерминированными и не учитывают нелинейность реальных объектов управления в указанной области [1]. Это приводит к снижению качества регулирования, увеличению времени и затрат на производство продукции.

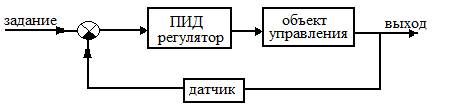
Рисунок 1. Схема управления на основе ПИД-регулятора

Поэтому достаточно активно ведутся исследования по модернизации представленной схемы управления, особенно в части регулятора. Существуют как схемы адаптивного управления, где данная адаптивность вносится как классическими методами, так и интеллектуальными, так и схемы, где регулятором выступает некоторая интеллектуальная система (нейронная сеть, нечеткая логика) [2].

Существуют два основных метода построения нечетких систем: Мамдани-Заде и Сугено-Такаги-Канга. В данной статье будет рассмотрен первый из них.

Построение системы нечеткого вывода включает в себя два этапа:

- определение функций принадлежности переменных;

- составление базы правил.

Общий логический вывод осуществляется за следующие пять этапов [3]:

В MATLAB разработан модуль fuzzy, обладающий интуитивно-понятным интерфейсом [4].

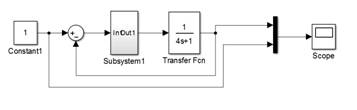
Рисунок 2. Модель системы управления на основе нечеткого ПИД-регулятора

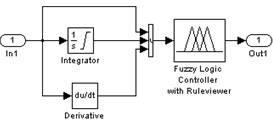
Рисунок 3. Блок регулятора

Командой fuzzy в окне MATLAB вызываем окно редактора фази-инференционной системы (Fuzzy Inference System Editor), выбираем тип системы - Мамдани, задаём три входа - для пропорциональной, интегральной и диффиренциальной составляющих и называем входные переменные P , I и D, а выходную - Out. Первоначально следует построить функции принадлежности входных и выходных переменных и правила нечеткого логического вывода [5].

Для описания переменных P, I, D выберем 3 треугольника (N, Z, P), для описания выходной переменной Out выберем 7 треугольников (NL, NM, N, Z, P, PM, PL). В этом же окне зададим диапазоны изменения переменных: Р – [-1, 1]; I – [-1 1]; D – [-1 1]; Out – [0 2] [6].

Следующим шагом необходимо задать лингвистические правила.

Чтобы предупредить увеличение сигнала рассогласования выходной сигнал регулятора должен увеличиваться при положительном значении скорости, и наоборот.

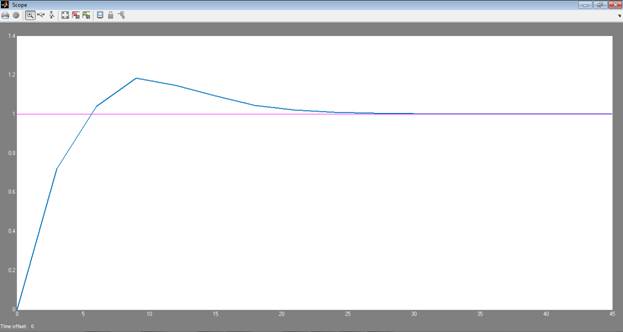
Рисунок 4. График переходного процесса с нечетким ПИД-регулятором

Таким образом, из результатов моделирования очевидно, что процесс устанавливается на заданном значении с небольшим перерегулированием.

Литература:

1. Аббасов И.Б. Двухмерное и трехмерное моделирование в 3ds MAX / И.Б. Аббасов. - М.: ДМК, 2012. - 176 c.

2. Авдеев В. Компьютерное моделирование цифровых устройств / В. Авдеев. - М.: ДМК, 2012. - 360 c.

3. Агравал Г.П. Системы автоматического управления: теория, применение, моделирование в MATLAB: Учебное пособие / Г.П. Агравал. - СПб.: Лань, 2013. - 208 c.