Математика/5. Математическое моделирование

,

Действительный член, профессор Российской Академии Естествознания (РАЕ), Почетный доктор наук (РАЕ), Заслуженный работник науки и образования,

к.т.н., доц. Буянкин В.М.

Московский Государственный технический университет имени. Н.Э. Баумана, Россия

Заслуженный работник науки и образования ( РАЕ), кан. физ-мат. наук ВАК РФ. Ковалева С.К.

РНЦ ” Курчатовский институт”

Моделирование системы нейросамонастройки токового контура электропривода

В статье рассматриваются вопросы синтеза нейрорегуляторов для систем управления электроприводами. Анализируются устойчивая работа и особенности применения нейрорегуляторов в замкнутых контурах. Нейрорегуляторы самонастраиваются при изменении параметров обьекта управления. Информация об изменении параметров обьекта управления сравнивается с оптимальными желаемыми характеристиками эталонной модели, вырабатывается сигналы обучения для нейрорегуляторов, которые обеспечивают необходимые оптимальные статические и динамические характеристики электропривода

Рассмотрим одноконтурную систему управления токовым контуром электродвигателя постоянного тока ПБСТ-22 с номинальными параметрами P=0,6кВт,

U= 110 В, I=7А, n=1000 об/мин, которая представлена на рис. 1

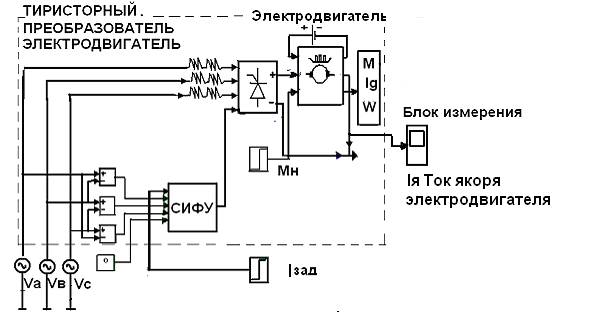
Рис. 1. Функциональная схема управления токовым контуром электродвигателем в среде MATLAB

Работу электропривода изображенной на рис. 1 можно описать системой линейных и нелинейных уравнений:

– Уравнение обмотки возбуждения

– Уравнение обмотки якоря

– Уравнение моментов на валу электродвигателя

(1)

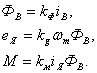
– Уравнение тиристорного преобразователя,

где – напряжение в обмотке возбуждения,

– ток возбуждения,

– активное сопротивление обмотки возбуждения,

– индуктивность обмотки возбуждения,

– магнитный поток обмотки возбуждения,

– напряжение на якоре,

– ток якоря,

– ЭДС якоря

– активное сопротивление якоря,

– индуктивность якоря,

J – момент инерции,

w – частота вращения электродвигателя,

М – вращающий момент электродвигателя,

– момент нагрузки,

– коэффициент ЭДС электродвигателя,

– коэффициент момента электродвигателя,

– амплитудное значение напряжения,

– угол поджигания тиристоров.

При помощи MATLAB с использованием выше описанной функциональной схемы электропривода можно смоделировать переходные процессы тока в токовом контуре при различных параметрах электродвигателя, которые описываются разностным уравнением.

(2)

Разработаем и обучим нейронную сеть для нейроиденгификации переходного процесса тока в электродвигателе, изображенной на рис. 2 Нейронная сеть имеет четыре нейрона во входном слое и один нейрон на выходе и описывается следующей системой уравнений:

– Выходной сигнал нейронной сети, задержанный на один такт

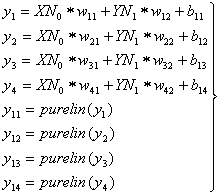(3)

–Уравнения первого входного слоя нейронной сети

– Уравнение второго выходного

слоя нейронной сети

-Выход нейронной сети

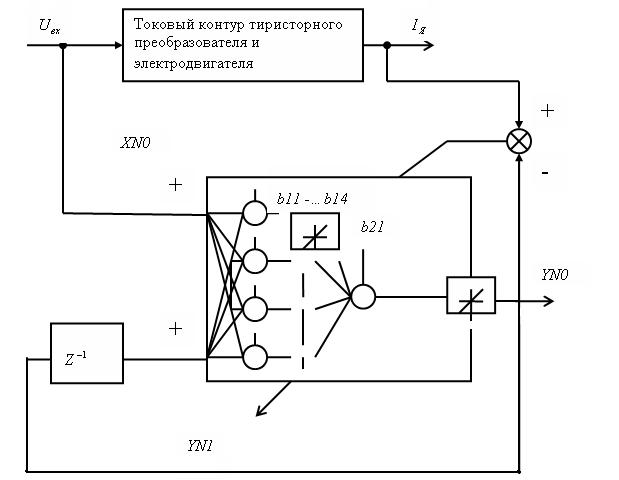
Рис. 2. Схема обучения нейронной сети

В результате обучения переходной процесс нейронной сети с необходимой заданной точностью повторяет переходной процесс тока, что позволяет сделать вывод об успешном решении задачи нейроидентификации.

Проведем нейросамонастойку в токовом контуре электропривода.

Структурная схема контура нейросамонастройки с блоком нейроидентификации представлена на рис. 3

.

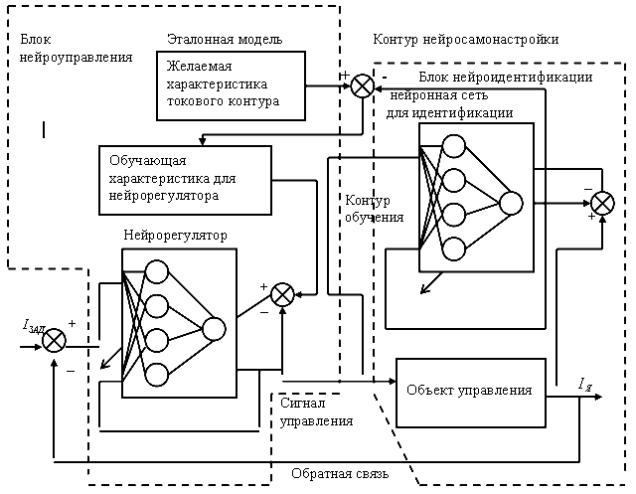
Рис. 3. Структурная схема контура нейросамонастройки

Контур нейросамонастойки состоит из эталонной модели с желаемыми характеристиками токового контура. Желаемый выходной сигнал описывается следующим разностным уравнением

(4)

Данные блока нейроидентификации сравниваются с данными эталонной модели, в результате сравнения получаются сигналы обучения для нейрорегулятора.

Нейрорегулятор рис. 4 имеет интегрально-пропорциональную структуру для выполнения роли компенсации электромагнитной постоянной времени электродвигателя, что существенно улучшает статические и динамические характеристики токового контура.

Уравнения ПИ- нейрорегулятора имеют следующий вид:

– сигнал на входе нейронной сети

– Сигнал на входе нейронной сети, задержанный на один такт

– Сигнал на выходе нейронной сети, задержанный на один такт 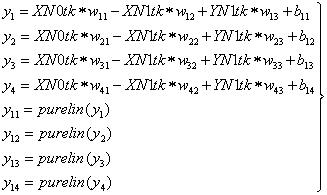–Уравнения первого входного слоя

нейронов

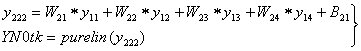–Уравнения второго выходного

слоя нейронов

(5)

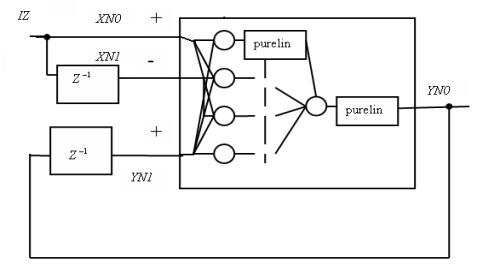
Рис. 4. ПИ- нейрорегулятор

Работа ПИ- нейрорегулятора в виде разностного уравнения имеет вид:

, (6)

где

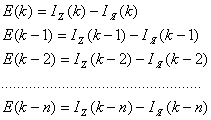
При разных индуктивностях и сопротивлениях якоря электродвигателя было получено семейство обучающих характеристик для ПИ- нейрорегулятора. В результате обучения нейрорегулятора токовый контур с нейросамонастройкой имеет переходной процесс совпадающий с желаемым переходным процессом эталонной модели. При изменении параметров электродвигателя блок нейроидентификации отслеживает эти изменения, сравнивает их с параметрами эталонной модели и вырабатывает обучающие характеристики для нейрорегулятора. В итоге переходной процесс токового контура при переменных и нелинейных параметрах электродвигателя остается как и прежде без изменений рис. 5.

Рис. 5. Переходные процессы изменения тока якоря электродвигателя в токовом контуре

Выводы

Таким образом система управления с нейроидентификацией с нейросамонастройкой и нейрорегулятором обеспечивает оптимальные статические и динамические характеристики работы электропривода при переменных и нелинейных параметрах электродвигателя.

Литература

1. Буянкин В.М. Интегральный, пропорциональный, дифференциальный нейрорегулятор. Вестник МГТУ им. Н.Э.Баумана, серия фундаментальные науки 2006 г.N3(64)

2. Буянкин В.М. Идентификация нейронной сетью электродвигателя постоянного тока в среде Matlab simulink Вестник МГТУ им. Н.Э.Баумана, серия приборостроение

2006 г.N3(22)

3. Буянкин В.М Нейроидентификация нейросамонастройка в электроприводе

Журнал «Нейрокомпьютер» 2006 г.N9

4.Буянкин В.М.,.Захаров В.Г Физические процессы нечеткого управления при обучении нейрорегуляторов токового контура электропривода с мягкими вычислениями Вестник МАДИ ГТУ N7