Математика/5. Математическое моделирование

Еличева Н.В., Базака Л.Н.

Задачи оптимизации. Методология создания индивидуализированных рационов питания спортсменов.

Полесский государственный университет, Беларусь

Построение рациона питания спортсмена с полным восполнением потребности в энергии, всех пищевых компонентах и поддержанием водного баланса организма - важное требование при организации тренировочного процесса. Особые физиологические условия, в которых находятся спортсмены, приводят к появлению у них дополнительных потребностей в тех или иных пищевых веществах. Особенности питания характерны для каждого вида спорта и связаны со спецификой физических нагрузок. Более того каждый спортсмен имеет персональные особенности метаболизма и физических нагрузок, что делает необходимым индивидуализацию питания. В связи с этим, одним из решений данной проблемы является разработка методологии создания индивидуализированных рационов питания.

Для анализа поставленной проблемы в работе был применен традиционный подход, основанный на использовании математических моделей вычислительных методов (методы оптимизации). Для решения задачи оптимизации рациона спортсменов была использована программа MS Excel. Так как данная программа имеет инструмент «Поиск решения», при помощи которого легко и быстро решаются задачи оптимизации.

В модель необходимо включать те параметры и переменные, которые оказывают влияние на рацион питания спортсмена.

Общее количество необходимой энергии рассчитывается по формуле:

, (1)

где

Епищ	- энергия, поступающая в организм из пищи (суточная калорийность питания);
Еосн.об	- энергия, которую организм расходует на основной обмен;
Ефиз нагр	-энергия, затрачиваемые на физическую активность;
Есддп.	- специфическое динамическое действие пищи - затраты энергии на переваривание, всасывание, транспорт и ассимиляцию нутриентов на уровне клетки;
Етерм	- термогенез - получение тепла для поддержания термостабильности в условиях меняющейся температуры окружающей среды.

Энергетические доли белков (Эб), жиров (Эж) и углеводов (Эу) в рационе :

Э_б = ЭТ_сут × ДЭ_б / 100; (2)

Э_ж = ЭТ_сут × ДЭ_ж /100; (3)

Э_у = ЭТ_сут × ДЭ_у / 100, (4)

где

Эб, Эж, Эу	- энергетические доли белков, жиров и углеводов в рационе;
ЭТсут	- суточные энерготраты;
ДЭб, ДЭж, ДЭу	- доля макронутриента в рационе питания, % от суточной калорийности.

Содержание основных пищевых веществ по массе в суточном рационе питания:

М_б = Э_б / ЭК_б; (5)

М_ж = Э_ж / ЭК_ж; (6)

М_у = Э_у / ЭК_у (7)

где

Мб, Мж, Му	- содержание основных пищевых веществ по массе в суточном рационе питания;
ЭКб, ЭКж, ЭКу	- количество энергии, получаемое при окислении 1 г макронутриента.

Для подбора необходимых блюд и продуктов используется технологическая база готовых блюд с названиями, их химическим составом и калорийностью и сведениями о технологии приготовления.

При построении модели были введены обозначения исходных данных. Условные обозначения исходных данных приведены в таблице 1.

Таблица 1 – Условные обозначения исходных данных

Обозначение	Параметр
aij (i=, j=)	содержание i-го питательного вещества в единице j-го продукта;
bi (i=)	минимальное содержание i-го питательного вещества в суточном рационе;
cj (j=)	цена единицы j-го продукта.

Стандартная математическая задача оптимизации сформулирована следующим образом. Пусть x₁ – это количество единиц 1-го продукта, x₂ – это количество единиц 2-го продукта, … x_n – это количество единиц n-го продукта, включаемые в рацион.

Стоимость рациона (целевая функция):

c₁x₁ + c₂x₂ +…+c_jx_j +…+c_nx_n→min (8)

Содержание первого питательного вещества в диете составит

a₁₁x₁+a₁₂x₂+…+a_1jх_j +…+a_1nx_n. (9)

и это количество должно быть не менее чем b₁ единиц:

a₁₁x₁+a₁₂x₂+…+a_1jх_j +…+a_1nx_n ≥ b₁. (10)

Аналогично составляем ограничения по всем видам питательных веществ:

a₂₁x₁ + a₂₂x₂ + …+a_2jх_j +…+a_2nx_n ³ b₂

_{……………………………………………………………….} (11)

a_m1x₁ + a_m2x₂ +…+a_mjх_j +…+a_mnx_n ³ b_m

Данная система ограничений может быть дополнена и другими неравенствами, если это продиктовано медицинскими требованиями.

Кроме того, x_j ³ 0, так как количество продуктов не может быть отрицательным числом.

С помощью инструмента «Поиск решения» была построена математическая модель данной задачи.

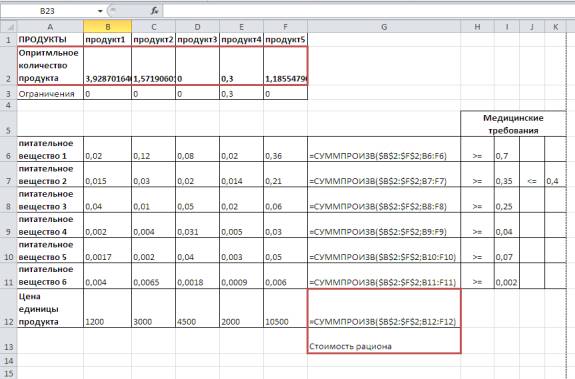
Рисунок 1 - Модель задачи

Современные математические методы, а также информационные технологии предоставляют инструменты для решения практических задач во многих областях человеческой деятельности, которые, на первый взгляд, далеки от классических представлений о математике.

Представленный метод составления рациона может быть использован не только в спорте, но и для реабилитации больных, для составления диет в детских учреждениях, больницах, домах для пожилых людей и т.д.

Литература:

1. Ларин Р.М., Плясунов А.В., Пяткин А.В. Методы оптимизации. Примеры и задачи: Учебное пособие. – Новосибирск: Новосибирский университет, 2003. – 115 с.

2. Орлов А.И. Теория принятий решений: Учебное пособие. – М.: Март, 2004.