Анализ универсальной структурной системы проф

Анализ универсальной структурной системы проф. Л.Т. Дворникова для механизмов высокого класса

К.ф.-м.н. Джанузаков С.Д.

Магистрант МУИТ Иманбаев А.К.

Магистрант МУИТ Сарсенбаев Д.А.

Основным из этапов создания механизма высокого класса, работающего с заданными входными и выходными данными, является синтез его структуры. Исходных данных необходимых для этого, часто представляется следующими параметрами:

• необходимой подвижностью механизма;

• количеством наложенных на систему связей;

• применяемой количеством звеньев

• допустимость класса применяемых кинематических пар ;

• ограничение на максимальную сложность звеньев.

Обеспечение выходных условий обеспечивает правильность подбора число звеньев сложной структуры , образующих механизм высокого класса, а также порядок и способ соединения их между собой.

Использование разного рода зависимости позволяет подбора числа звеньев не превышая требуемой данной сложности который является одним из основным из важных моментов, количество видов кинематических пар, разрешаемые к применению.

Профессором Л.Т. Дворниковым разработан теории структур механизмов в целом и в том числе теории структур механизмов высокого класса. При заданных условиях он объединяя несколько зависимостей, связывая число звеньев различной сложности и общим числом кинематических пар того или иного вида получил универсальной систему уравнений, названную им универсальной структурной системой [1,2].

+ + + + + ( 1)

= -

Здесь: n – общее число звеньев;

W – подвижность системы;

m – число наложенных на систему связей;

k – ограничение на классы применяемых кинематических пар;

p_k– число кинематических пар того или иного класса;

τ – количество вершин наиболее сложного звена;

, , , – числа звеньев различной сложности;

( 2)

Система рассмотренная выше является нестандартной, от вычисления к вычислению , количество одночленов в правой и левой части, число искомой неизвестной могут меняться. Следствием этого является, что количество неизвестных может превышать количеством уравнений системы. Значение неизвестных только целочисленные.

Сложность решение системы заключается в следующем, при небольшом количестве звеньев решение получается достаточно просто, а как увеличивается общее число звеньев механизма методы решения становиться не тривиальным.

Теоретически такие задачи решаются методом перебора возможных вариантов чисел звеньев . С увеличением общее число звеньев решение задачи почти невозможно без применения компьютерных программ.

В работе [2] отмечен, что метод перебора не дают ожидаемых результатов, это связано с перебором огромного количества исследуемых возможных вариантов. В связи с этой проблемой для поиска целочисленного решения используем следующий алгоритм:

Шаг1. Находим неизвестные и определяем количество неизвестных. При этом учитываем область определения правой части. Определим перебор вариантов. Строим гиперкуб.

Неизвестные- , …, ,

Общее количество неизвестных-

Правая часть принимает значение от нуля до

Набор звеньев не более-

Количество ребер-

В дискретном пространстве строим гиперкуб размерности и длиной ребра

Шаг2. Определяем количество звеньев у которых сумма значении не равно общему. Найденный узел исключаем из рассмотрения.

Шаг3. Находим общее количество кинематических пар. Определяем длину ребра виртуального гиперкуба. Подставляя в правую часть первое уравнение находится набор чисел звеньев общее количество кинематических пар. Из первого уравнения системы можно определить длину ребра виртуального гиперкуба как общее число кинематических пар.

Шаг4. Проверяется тождественность третьего уравнения системы.

Шаг5. Обращаясь к третьему уравнению, уравнению набора звеньев и кинематических пар, находится решение.

Заметим первое уравнение системы можно брать в качестве виртуального счетчика. По аналогии представления система чисел в конкретной системе счисления, которое записывается в виде следующей формулы:

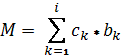
Где М- рассматриваемое в системе счисления число, i –количество разрядов, –значение k- го разряда, вес k- го разряда.

Если добавить в младший разряд выше указанного счетчика тогда можно обеспечить полную выборку всевозможных вариантов наборов звеньев.

На основание выше алгоритма разработан модуль разрешающий задачу

об определения числа звеньев, кинематических пар механизмов высокого класса.

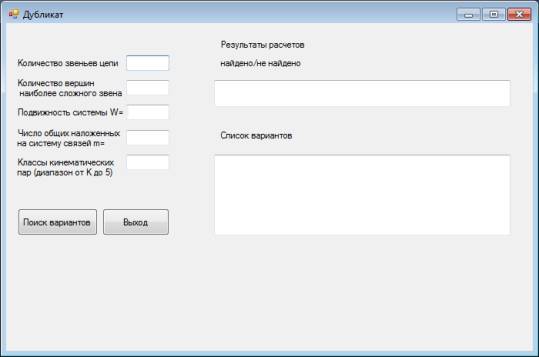
Приводится фрагмент программы следующего модуля

начало

Public Class Form1

Private Sub Button1_Click(ByVal sender As System.Object,

ByVal e As System.EventArgs) Handles Button1.Click

Dim no, tau, W, m, kmin As Double

no = CDbl(TextBox1.Text())

tau = CDbl(TextBox2.Text())

W = CDbl(TextBox3.Text())

m = CDbl(TextBox4.Text())

kmin = CDbl(TextBox5.Text())

Dim kolvar, ni(5000), pk(5000), sum1, sum2, sum3, sum4 As Double

Dim i As Integer

Dim stroka As Char

TextBox7.Text() = ""

For i = 1 To tau Step 1

ni(i) = 0

ni(1) = no - 1

While ni(tau) < 0

sum1 = 1

For i = 1 To (tau - 1) Step 1

sum1 = sum1 + ni(i)

If sum1 <> no Then

Exit While

End If

sum2 = tau

For i = 1 To tau - 1 Step 1

sum2 = sum2 + i * ni(i)

For i = 1 To 6 Step 1

pk(i) = 0

pk(kmin) = sum2

продолжение

While pk(6) < 0

sum3 = 0

For i = 1 To 5 Step 1

sum3 = sum3 + pk(i)

If sum3 = sum2 Then

sum4 = 0

For i = kmin To 5 Step 1

sum4 = (-sum4 + (i - m) * pk(i))

If ((6 - m) * sum1 - sum4) = W Then

kolvar = kolvar + 1

stroka = ""

End If

pk(kmin) = pk(kmin) + 1

For i = kmin To 5 Step 1

If pk(i) = sum2 + 1 Then

pk(i) = 0

pk(i + 1) = pk(i + 1) + 1

End If

End While

ni(1) = ni(1) + 1

For i = 1 To tau - 1 Step 1

If ni(i) = no + 1 Then

ni(i) = 0

ni(i + 1) = ni(i + 1) + 1

End If

End While

End Sub

End Class

СПИСОК ЛИТЕРАТУРЫ

1. Дворников Л.Т. Начала теории структуры механизмов: Учебное пособие/ Новокузнецк, СибГГ-МА, 1994. – 102 с.

2. Степанов А.В. Решение универсальной структурной системы проф. Л.Т. Дворникова Вестн. Куз-ГТУ. 2007, №3.С.43-47.