Технические науки/12. Автоматизированные системы управления

Доцент БЕГОЯН К.В.

Национальный политехнический университет Армении, Ереван, Армения

Определение передаточной функции понижающего преобразователя постоянного напряжения с сопротивлением в цепи конденсатора

Понижающие преобразователи постоянного напряжения (ППН) с использованием широтно-импульсной модуляции (ШИМ) сигнала широко применяются в различных технических приложениях (рис. 1) [1,2]. При достаточно высокой частоте прерывания , среднее за период значение выходного напряжения равно , где есть напряжение источника питания, а называется коэффициентом заполнения импульсов.

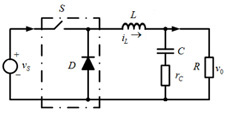
Рис. 1. Схема понижающего ППН с сопротивлением

В статье дается вывод передаточной функции понижающего ППН в режиме непрерывных токов при наличии дополнительного сопротивления в цепи конденсатора. Знание этой передаточной функции при малых отклонениях сигналов от их средних значений необходимо для исследования систем управления (например, систем управления двигателей постоянного тока), в которых эти преобразователи входят как управляющие элементы.

2. Уравнения динамики ППН в пространстве состояний. Импульсные ППН с ШИМ являются нелинейными нестационарными системами с периодическими параметрами. Поэтому точное аналитическое исследование их динамики является исключительно сложной задачей. На практике обычно прибегают к специальным приближенным методам, среди которых можно выделить метод, основанный на таком преобразовании уравнений ППН в пространстве состояний, при которых эти уравнения правильно описывают усредненную во времени динамику преобразователя [3].

Выберем в качестве переменных состояния ППН ток дросселя и напряжение на конденсаторе . Тогда, вводя в рассмотрение двумерный вектор-столбец с координатами и , для схемы на рис. 1 (т.е. для интервала замыкания ключа ) можно записать

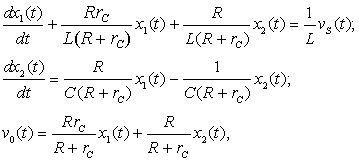(1)

или, в векторно-матричной форме,

(2)

где

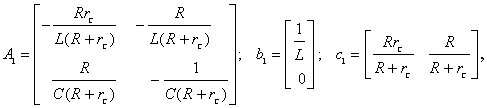(3)

а входная функция отражает тот факт, что напряжение питания может меняться во времени. Соответствующие векторные уравнения для интервала , при котором электронный ключ разомкнут, имеют аналогичный вид

(4)

Нетрудно показать, что матрица и векторы и в (4) даются выражениями

Вводя в рассмотрение функцию переключения [1,3]

(5)

дифференциальные уравнения ППН на рис. 1 можно записать в виде

(6)

которые сводятся, с учетом того, что к простому виду

(7)

Таким образом, нами получены точные дифференциальные уравнения ППН в пространстве состояний (7), зависящие от функции переключения (5), значение которой скачкообразно переходит от единицы к нулю и обратно в моменты замыкания и размыкания электронного ключа. В соответствии с методом усреднения уравнений динамики в пространстве состояний, на первом этапе осуществляется усреднение по времени функции переключения (1) [1]. Для этого вводится функция времени

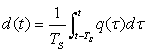, (8)

которая представляет собой усредненное за период выражение для при непрерывном изменении времени . Далее осуществляется, с учетом (8), усреднение по времени точных уравнений динамики (7), что дает

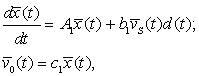(9)

где усредненные переменные , и определяются выражениями, аналогичными (8), и предполагается, что вектор и функция не очень отличаются от своих усредненных значений [1-3]. Уравнения (9) называются усредненной моделью ППН в пространстве состояний. Для вывода передаточных функций ППН следует осуществить линеаризацию нелинейной усредненной модели в окрестности некоторой постоянной рабочей точки [1]. Классическая процедура линеаризации заключается в разложении, считая отклонения от рабочей точки малыми, нелинейной функции в ряд Тейлора и пренебрежении всеми членами кроме линейного [4]. Однако вид уравнений (9) позволяет упростить эту процедуру. Представим все усредненные функции времени в (9) в виде

, (10)

где все отклонения считаются малыми. Тогда, подставив (10) в (9) и разделяя переменные, приходим к уравнениям

(11)

для постоянных установившихся состояний, и

(12)

для малых отклонений переменных усредненной модели от рабочей точки.

Легко видеть, что единственным нелинейным членом в уравнениях (12) является член, заключенный в квадратные скобки и содержащий произведение малых величин и . Пренебрегая этим членом, окончательно получим линеаризованные уравнения усредненной модели ППН в виде

(13)

Следуя стандартной методике получения передаточных функций линейных систем из уравнений в пространстве состояний [4], нужно осуществить преобразование Лапласа уравнений (13) при нулевых начальных условиях и исключить из полученных алгебраических уравнений вектор состояний , где - переменная Лапласа. Это дает следующее комплексное уравнение относительно скалярной выходной переменной :

, (14)

что приводит к двум скалярным передаточным функциям ППН относительно независимых входных переменных и :

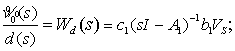
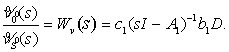(15)

Как видно из (15), передаточные функции и отличаются лишь постоянными коэффициентами и Подставив (3) в (15) получим

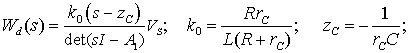(16)

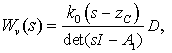(17)

где

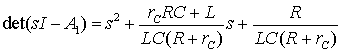. (18)

Таким образом, ППН на рис. 1 описывается передаточными функциями второго порядка, имеющими в общем случае нуль в точке , определяемой емкостью и сопротивлением в цепи конденсатора. Укажем, что в случае идеального ППН, т.е. при , нули передаточных функций отсутствуют [1,2].

Пример. Рассмотрим ППН с параметрами , . Передаточная функция (16) при этих параметрах равна

(19)

и имеет два комплексно-сопряженных полюса , а также один нуль . Отметим, что передаточная функция (16) в данном случае отличается от (19) только постоянным коэффициентом 0.078125. На рис. 2 показаны диаграммы Боде передаточной функции (19). Как видно из рис. 2, фазовая характеристика идеального ППН при стремится к , т.е. наличие сопротивления улучшает запасы устойчивости понижающего ППН, что, в свою очередь, приводит к лучшим динамическим характеристиками преобразователя (в случае идеального ППН, т.е. при , фазовая характеристика при стремится к ). Данное обстоятельство имеет важное значение при использовании ППН в замкнутом контуре систем управления.

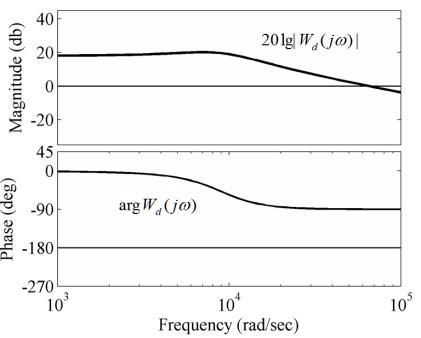
Рис. 2. Диаграммы Боде понижающего ППН с передаточной функцией (19)

СПИСОК ЛИТЕРАТУРЫ

1. Choi B., Pulse-width Modulated DC-to-DC Power: Conversion Circuits, Dynamics, and Control Designs, A John Wiley and Sons, Inc., Hoboken, New Jersey, 2008, 649 pp.

2. Mohan N., M. Tore, P. Willam, Power Electronics: Converters, Applications, and Design, John Wily and Sons, Ltd, New York, 2002, 802 pp.

3. Middlebrook R., Cuk S., A General Unified Approach to Modeling Switching Converter Power Stages, IEEE Power Electronics Specialists Conference Record, pp. 18-34, 1976.

4. Dorf R., Bishop R. Modern Control Systems. Addison-Wesley Publishing Co., Reading, MA, 2007. 1046 pp.