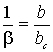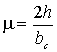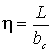К.т.н. Волков В.П.,
к.т.н. Земцова О.Г., Волкова О.В.
Пензенский
государственный университет архитектуры и строительства, Россия
Вычисление геометрических
характеристик Z-образного профиля с использованием безразмерных коэффициентов
Для
определения несущей способности при расчете на прочность, жесткость и
устойчивость тонкостенного стержня Z-образного профиля необходимо определение его геометрических
характеристик. Исследуем зависимость между геометрическими размерами Z-образного
профиля и его геометрическими характеристиками для определения положения
главных центральных осей такого сечения стержня.
В более ранних работах авторами был введен
безразмерный коэффициент ξ, характеризующий отношение длины свеса полки к
полной длине профиля:
(1)
где
– полная длина Z-образного профиля. Диапазон изменения относительной длины свеса полки [4]:
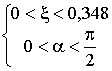(2)
Тогда математически постановку задачи можно
описать следующим образом: при какой величине коэффициента ξ оси XY являются главными
центральными осями сечения, т.е. необходимо найти угол α. Принять толщину δ<<h, b (рис.1). Все оси, проходящие через
центр тяжести С, являются
центральными осями, т.к. данная форма сечения имеет центральную симметрию.
Оси XY являются главными
осями, если центробежный момент инерции сечения равен нулю, т.е.
(3)
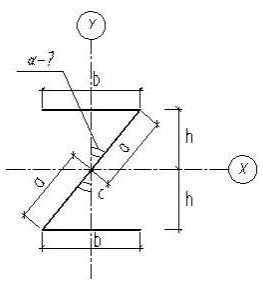
Рис.1
Введем обозначения (рис.2):
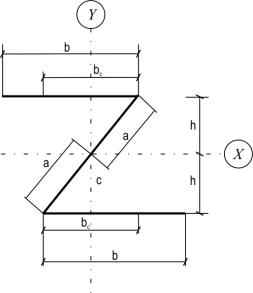
Рис.
2
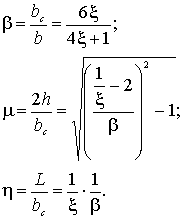(4)
С
учетом обозначений (4) осевой момент инерции:
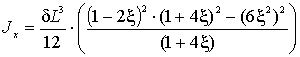. (5)
осевой момент сопротивления:
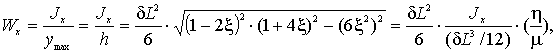(6)
причем при ξ= 0,1184 имеем Wx
= Wmax.
Формулы (5) и (6) можно существенно упростить,
если ввести безразмерные коэффициенты
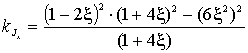(7)
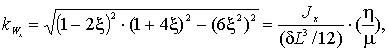(8)
Тогда
, 
Значения коэффициентов (7) и (8) для наиболее
часто используемых значений коэффициента ξ вычислены и приведены в табл.1.
Таблица
1
|
|
|
|
|
|
|
|
0,1 |
2,3333 |
18,64 |
23,333 |
0,8934 |
1,1184 |
|
0,1184 |
2,0743 |
13,333 |
17,5194 |
0,8535 |
1,1215 |
|
0,15 |
1,7778 |
8,2358 |
11,852 |
0,7726 |
1,1118 |
|
0,2 |
1,5 |
4,3875 |
7,5 |
0,616 |
1,053 |
|
0,21 |
1,4603 |
3,9073 |
6,9538 |
0,5809 |
1,0339 |
|
0,22 |
1,4242 |
3,4847 |
6,4738 |
0,5447 |
1,0120 |
|
0,23 |
1,3913 |
3,1097 |
6,0491 |
0,5074 |
0,987 |
|
0,24 |
1,3611 |
2,7744 |
5,6713 |
0,4691 |
0,9588 |
|
0,25 |
1,3333 |
2,4721 |
5,3333 |
0,4297 |
0,927 |
|
0,26 |
1,3077 |
2,1974 |
5,0296 |
0,3894 |
0,8912 |
|
0,27 |
1,284 |
1,9455 |
4,7556 |
0,3482 |
0,8851 |
|
0,28 |
1,2619 |
1,7124 |
4,5068 |
0,3061 |
0,8055 |
|
0,29 |
1,2414 |
1,4941 |
4,2807 |
0,2632 |
0,7539 |
|
0,30 |
1,2222 |
1,2867 |
4,074 |
0,2195 |
0,6948 |
|
0,31 |
1,2043 |
1,0859 |
3,8848 |
0,1750 |
0,6262 |
|
0,3143 |
1,1969 |
1,0003 |
3,8081 |
0,1557 |
0,5928 |
|
0,32 |
1,1875 |
0,8859 |
3,7109 |
0,1299 |
0,5443 |
|
0,33 |
1,1717 |
0,6763 |
3,5506 |
0,08417 |
0,4419 |
|
0,34 |
1,1569 |
0,4307 |
3,4026 |
0,03782 |
0,2987 |
|
0,345 |
1,1498 |
0,2595 |
3,3328 |
0,01443 |
0,1853 |
Таким
образом, решение жесткостной и прочностной задач для тонкостенных стержней Z-образного
профиля можно существенно упростить,
если ввести безразмерные коэффициенты ξ, 
, 
для нахождения
геометрических характеристик сечения.
Литература:
1. Александров
А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. М:
Высш. шк., 1995. 560 с.
2. Власов
В.З. Избранные труды. В 3 т. / Т.2 Тонкостенные упругие стержни. Принципы
построения общей технической теории оболочек. М.: Изд-во АН СССР, 1963. 507с.
3. Шеин
А.И., Земцова О.Г. Снижение уровня колебаний системы «упругое основание –
высотное сооружение» с помощью нелинейного динамического гасителя //
Региональная архитектура и строительство. 2011. № 2. С. 83-90.
4. Волков
В.П., Земцова О.Г., Волкова О.В. Определение диапазон изменения относительной
длины свеса полки Z-образного профиля // Научное пространство Европы–2015.
2015. [Электронный ресурс]. URL: http://www.rusnauka.com/Page_ru.htm (дата
обращения: 10.04.2015).