А. А. Шкаликов, Л. К. Кусаинова, А. Ж. Монашова

 

О СПЕКТРЕ ОДНОГО НЕСАМОСОПРЯЖЕННОГО ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА ВТОРОГО ПОРЯДКА НА ПОЛУОСИ

 

Евразийский национальный университет имени Л.Н. Гумилёва

 

Пусть  - гильбертово пространство функций , , с конечной нормой

                                  

В работе изучается оператор , порождаемый в  дифференциальным выражением

                                      

где  и  - комплекснозначные локально суммируемые в  функции. Пусть , . Ниже всюду будем предполагать выполненными следующие условия:

Обозначим через  пополнеие класса  по норме , где

                                

Здесь  - класс финитных в  и бесконечно дифференцируемых функций.  Оператор  задается условиями

                                     

В настоящей работе мы показываем, что  имеет компактную резольвенту и получаем двусторонние оценки для функции  равной сумме кратностей всех собственных чисел , лежащих в угле

                          

Известно что условия  и  обеспечивают компактное вложение

Соответственно оператор , ассоциированный с формой  в следующем смысле:

                                                                   

 имеет вполне непрерывный обратный . При этом , а область значения . См [1, п.2.2] и [2].

Пусть  - локально суммируемая в  функция, имеющая  М. Отелбаевым для оператора Штурма-Лиувилля с потенциалом  были получены двусторонние оценки распределения собственных чисел [1, п.2.2]. Исходя из них мы можем утверждать, что справедливы неравенства:

                                                                 

 В (2) приняты обозначения:  при ,  - четное продолжение  на все , ,

 

                                  

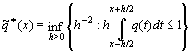
- “среднее Отелбаева”. Заметим сразу, что

                                                                   

 К тому же, очевидно, что  при . 

 

 Теорема 1 1 Справедлива оценка

                                                                                         

 

 где  - абсолютная постоянная.

Положим   

 

 Теорема 2 2 Пусть

                                                                                   

 

 Тогда

                                                                                         

 

 Следствие 13  Пусть выполнено условие (5). Тогда

                               

 

 

 Теорема 34  Пусть выполнено следующее условие:

                                                                                 

 Тогда   

 

 Следствие 25  Пусть выполнено условие (7). Тогда справедливы оценки:

                               

 

 

Приступим к кратким доказательствам результатов работы. Обозначим через  пополнение пространства  по отрицательной норме Лакса

                                         

Здесь  - единичный шар пространства  с нормой . Справедливо неравенство типа Коши:

                                                                   

 К тому же, как следует из (8), равенство

                                                       

 задает на прямом произведении  невырожденную билинейную форму. Обозначим через  пространство, сильно сопряженное к нормированному пространству . Следующие утверждения доказываются стандартными рассуждениями, cм. [3]. 

 

 Лемма 6  a)  Пространство  плотно в .

b)  Существует сопряженно-линейная биекция  такая, что

                                                       

 c)  Существует сопряженно-линейная биекция  такая, что

                                                                                  

 d)    

 

Опираясь на утверждение b) леммы 1 мы можем задать на  скалярное произведение  согласованное в силу (10) с нормой . 

 

 Лемма 7  Оператор  самосопряжен.  

 Доказательство. Сопряженный к  оператор  определяется условиями:

                               

 Из утверждений леммы 1 следует, что условие (12) перейдет в следующее:  где  единственным образом определяется по  и . Так как  плотно в , то  и  Отождествляя  с , получим

 

 Лемма 8  Оператор  может быть продолжен до вполне непрерывного оператора   

 Доказательство. Поскольку

                                                                   

  то  есть биекция с нормой . Для обратного оператора  в силу (13) на каждом  

                                                               

  откуда следует, что  также есть биекция  на  с нормой . Для каждого  с нормой  в силу (13) и (14)

                          

 

                       

 

                                         

Итак,  есть ограниченный оператор на плотном в  линейном многообразии  и может быть продолжено на все  посредством равенства

                                

Докажем, что  как оператор из , вполне непрерывен. Пусть  - оператор, сопряженный к . Поскольку , то можно считать, что  и  для . При этом . В силу последного . Следовательно,  содержится в шаре , а так как  предкомпактен в , то из  можно выделить сходящуюся в  подпоследовательность . Если мы возьмем , то ввиду полноты  в  для произвольного  и каждого  найдется аппроксимирующий элемент  такой, что . Далее выписываем оценки  из которых следует, что  при .

 

 Лемма 9 [4] Оператор  продолжается до компактного оператора .  

 

Доказательство теоремы 1. Из лемм 2-4 следует, что оператор  и удовлетворяет условиям теоремы 8.2 [5]. Выпишем важную для нас оценку , полученную в указанной теореме:

                                                         

 где  - абсолютная постоянная, а  не зависит от  и . Из неравенств (2) и (15) следует справедливость оценки

                                                 

 Осталось перейти к верхнему пределу в (16) при .

Доказательство теоремы 2 опирается на импликацию

                                                             

 вытекающего из теоремы 8.3 в работе [5]. Для нас, в силу оценки (2) основным является доказательство того, что выполнено условие импликации (17). Из (3) легко вывести оценку  Полученная оценка вместе с (2) влечет за собой неравенства:  

                    

Теорема 3 есть прямое следствие теоремы 8.4 из работы [5].

 

 

Литература

1.  М. О. Отелбаев  Оценки спектра оператора Штурма-Лиувилля  Алма-Ата  Гылым  1990

2.  К. Т. Мынбаев, М. О. Отелбаев  Весовые функциональные пространства и спектр дифференциальных операторов  М.  Наука  1988

3.  К. Иосида  Функциональный анализ  М.  Мир  1967

4.  А. Ж. Монашова  Об одном компактном возмущении несамосопряженного оператора второго порядка  Астана  Вестник. Научный журнал.  2010

5.  А. С. Маркус  Введение в спектральную теорию полиномиальных операторных пучков  К.  Штиинца  1986