УДК 541.135.4

ГРАНИЦА БЛОКИРОВАННЫЙ (ИНЕРТНЫЙ) ЭЛЕКТРОД / ТВЕРДЫЙ ЭЛЕКТРОЛИТ В ХРОНОАМПЕРОМЕТРИЧЕСКОМ И ХРОНОПОТЕНЦИОМЕТРИЧЕСКОМ РЕЖИМАХ ЗАРЯЖЕНИЯ

Р.М.Гусейнов, Р.А.Раджабов

Дагестанский государственный педагогический университет

367003, Махачкала, ул.М.Ярагского, 57, Россия

Методом операционного импеданса в двух режимах (хроноамперометрическом и хронопотенциометрическом) исследована кинетика процесса заряжения границы блокированный (инертный) электрод/ твердый электролит в случае малых и больших времен заряжения. Анализируется случай замедленной диффузии и адсорбции – десорбции одного сорта частиц – дефектов жесткой подрешетки твердого электролита (неосновных носителей тока). Показано, что в хронопотенциометрическом режиме аналитические соотношения ток-время функционально отличаются друг от друга в случае малых времен заряжения – с одной стороны, и в случае больших времен заряжения – с другой. В хроноаперометрическом режиме установлено, что формирование двойного электрического слоя на границе блокированный электрод/твердый электролит при больших временах происходит значительно быстрее, чем при малых временах.

Ключевые слова: твердый электролит; блокированный электрод; операционный импеданс; двойной электрический слой; эквивалентная электрическая схема.

Введение

Граница инертный (блокированный) электрод / твердый электролит (ТЭЛ), на которой происходит формирование двойного электрического слоя (ДЭС), является обязательным элементом большинства электрохимических приборов на основе ТЭЛ. Так как многие электрохимические устройства подобного типа работают в режимах ступенчатого изменения (включения) тока или потенциала, успехи в разработке этих приборов связаны с всесторонним исследованием кинетики нестационарных процессов образования ДЭС, влияния на них параметров ТЭЛ, а также материала электрода и частоты переменного напряжения [1,2]. Кинетика формирования ДЭС на исследуемой границе в режимах линейной развертки тока и потенциала нами была анализирована ранее [3]. Вданной работе мы приводим результаты исследования поведения границы блокированный электрод / твердый электролит в хроноамперометрическом и хронопотенциометрическом режимах заряжения.

Поскольку в формировании двойного электрического слоя принимает участие не только быстрая (основные ионы проводимости, например, Ag⁺ в Ag₄RbI₅), но и медленная подсистема (дефекты анионной подрешетки, например, ионы I^-), то нам необходимо исследование релаксационного поведения системы как для малых, так и для относительно больших времен заряжения границы инертный электрод/твердый электролит.

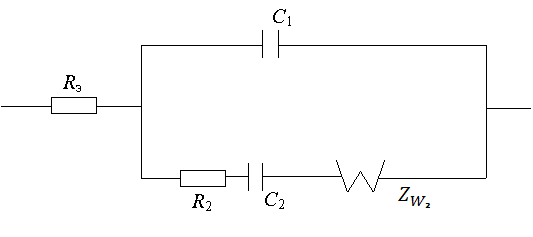
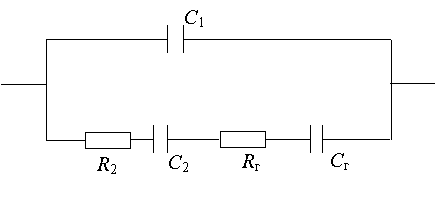
Эквивалентная электрическая схема ячейки с границей блокированный (инертный) электрод/ твердый электролит в случае замедленной диффузии и адсорбции-десорбции одного сорта частиц (а именно, дефектов жесткой подрешетки твердого электролита), согласно [1,2], может быть изображена в виде цепи (рис.1), где R_э – сопротивление твердого электролита; C₁ - емкость адсорбции-десорбции, обусловленная быстрыми (основными) ионами проводимости твердого электролита (например, ионами Ag⁺ в Ag₄RbI₅); R₂ и C₂ – соответственно сопротивление и емкость адсорбции-десорбции, связанные с дефектами жесткой части решетки твердого электролита (например, ионами I^-); – диффузионный импеданс Варбурга, связанный с дефектами решетки твердого электролита.

1.Теоретический анализ

1.1.Случай малых времен заряжения

Операционный импеданс ячейки, согласно эквивалентной электрической схеме рисунка 1, может быть записан в виде:

(1)

где - оператор Лапласа. В рассматриваемом нами случае сопротивление твердого электролита R_э принято равным нулю.

Примером анализируемой нами электрохимической системы может служить ячейка типа (-)Ag/Ag₄RbI₅/СУ(+), где СУ – инертный (блокированный) электрод из стеклоуглерода, графита или платины;

Ag₄RbI₅ – твердый электролит.

1.1.1.Хроноамперометрический режим

В хроноамперометрическом режиме i(t)=const, поэтому оператор тока (по Лапласу) i(p)= i/p. По определению, операторный потенциал , поэтому подставляя в последнее соотношение значения и , получим

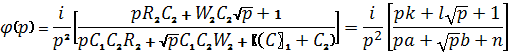(2)

В выражение (2) введены обозначения:

а = С₁ С₂ R₂; b= С₁ С₂W₂; n = С₁+ С₂; k = R₂ С₂ ; l = W₂С₂.

Все члены как числителя, так и знаменателя в выражении (2) разделим на множитель а, и тогда оно перейдет в выражение (2а)

, (2а)

где ; ; ; ;

Разложим выражение (2а) как дробно-рациональное на сумму простейших

, (3)

где m₁ и m₂ – корни (нули) характеристического уравнения второй степени , равные .

Согласно теореме Виета имеем соотношения ; . Коэффициенты d₁, d₂, d₃, d₄ и d₅ в уравнении (3) могут быть найдены путем приравнивания множителей при одинаковых степенях р в числителях слева и справа [4]. Найденные таким путем значения коэффициентов d₁, d₂, d₃, d₄ и d₅ равны:

;

;

; (4)

;

.

С помощью таблиц обратного преобразования Лапласа [4,5] можно выполнить по членный переход выражения (3) в пространство оригиналов, в результате чего получим для потенциала следующее выражение

(5)

С учетом соотношения выражение (5) значительно упрощается и тогда для имеем

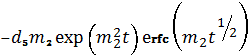, (6)

где – функция, называемая дополнительным интегралом вероятностей; – функция ошибок, значения которой при различных x приведены в справочниках [5,6,7].

Следует отметить, что при больших величинах значения членов в уравнении (6), содержащих функции , сводятся к нулю. В этих условиях реальный смысл будут иметь первые два члена в выражении (6) для потенциала.

График зависимости потенциал – время, построенный в соответствии с уравнением (6), представлен на рис.2 (кривая 1).

Что касается верхнего предела потенциала заряжения границы блокированный электрод / твердый электролит, то он должен быть ограничен потенциалом разложения твердого электролита.

Из рисунка 2 (кривая 1)и уравнения (6) следует, что тангенс угла наклона кривой 1 равен

, (7)

так что суммарная емкость С₁ и С₂, т.е. (С₁ + С₂) можно вычислить по соотношению

(8)

1.1.2.Хронопотенциометрический режим

В хронопотенциометрическом режиме φ(t)=const, поэтому оператор потенциала по Лапласу φ(p)= φ/p.

По определению, операторный ток поэтому подставляя в последнее соотношение значения , получим

, (9)

где

а = С₁ С₂ R₂;

b = С₁ С₂W₂;

k = R₂ С₂;

l = W₂С₂;

n = С₁+ С₂.

Все члены как числителя, так и знаменателя в выражении (9) разделим на множитель k, и тогда уравнение (9) переходит в уравнение (10)

, (10)

где ; ; ; ; ;

Разложим уравнение (10) как дробно-рациональное выражение на сумму простейших

, (11)

где m₁ и m₂ – корни (нули) характеристического уравнения второй степени

, равные .

С другой стороны, согласно теореме Виета имеем соотношения ; .

Коэффициенты d₁ и d₂ в уравнении (11) могут быть найдены путем приравнивания множителей при одинаковых степенях р в числителях слева и справа [4]. Найденные таким путем значения коэффициентов d₁ и d₂ равны:

; .

С помощью таблиц обратного преобразования Лапласа [4,5] можно выполнить по членный переход выражения (11) в пространство оригиналов, в результате чего получим для тока следующее выражение

, (12)

где

Для оценки корней квадратного уравнения и будем исходить из тех же значений параметров эквивалентной электрической схемы, что были использованы нами и в хроноамперометрическом режиме, а именно:

; ; ; ; .

Используемые нами значения параметров эквивалентной электрической схемы соответствуют действительным (реальным) экспериментальным данным, полученным для подобных систем Е.А. Укше и Н.Г. Букун классическим импедансным методом [1].

Корни квадратного уравнения и при указанных выше значениях параметров эквивалентной электрической схемы оказываются действительными и равными ; .

При этих значениях и два последних члена в уравнении (12) содержащие , превращаются в нули, а реальный смысл будут иметь первые два члена для тока.

Графики зависимости тока заряжения от времени в координатах и представлены на рисунках 3 и 4. Из рисунка 4 по величине тангенса угла наклона прямой можно определить также параметры эквивалентной цепи, как , и .

1.2. Случай больших времен заряжения

Согласно Джекобсону и Весту [8], диффузионный импеданс может быть смоделирован последовательным соединением активного сопротивления и емкости . Поэтому эквивалентная электрическая схема ячейки с границей блокированный электрод / твердый электролит в случае всех трех типов электродов (плоского, цилиндрического и сферического) и больших времен заряжения может быть представлена в виде схемы, изображенной на рис.5.

Операционный импеданс ячейки, соответствующий схеме, изображенной на рис. 5, может быть записан в виде

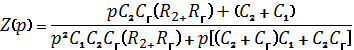, (13)

где R_г и С_г – соответственно сопротивление и емкость, обусловленные геометрической формой электродов (для сферического или цилиндрического электрода); параметры С₁ , С₂ и R₂ имеют свое обычное значение (смотрите стр. 2 настоящей статьи).

1.2.1. Хроноамперометрический режим

В хроноамперометрическом режиме для операционного потенциала, согласно выражению , получим

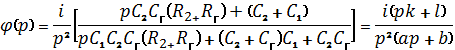(14)

В выражение (14) введены обозначения:

а = С₁ С₂ С_г (R₂ + R_г); b= (С_г + С₂ ) С₁ + С₂ С_г; k = С₂ С_г (R₂ + R_г); l = С₁ + С₂.

Для удобства преобразования операторного потенциала в область оригиналов выражение (14) целесообразно привести к следующему виду

, (15)

где ; ; .

Коэффициенты d₁, d₂ и d₃, найденные описанным нами ранее способом, равны:

;

;

С помощью таблиц обратного преобразования Лапласа для потенциала находим следующее выражение

(16)

На рисунке 2 приводится график зависимости потенциала от времени заряжения границы блокированный электрод / твердый электролит (кривая 2), построенный в соответствии с уравнением (16) при следующих значениях параметров эквивалентной электрической схемы:

; ; ; ; ; .

При этом параметр приобретает достаточно большое значение, так что третий член в уравнении (16) стремится к нулю. Что касается значений коэффициентов d₃ и d₂ (d₂=-d₃), то они по своей величине на 4 порядка меньше (d₂ = 13,84 10^-4 мВ), чем значение коэффициента d₁=84 мВ/с. Таким образом, при реальных значениях параметров исследуемых на практике электрохимических систем потенциал блокированного электрода определяется первым членом в выражении (16).

1.2.2.Хронопотенциометрический режим

В хронопотенциометрическом режиме для операторного тока, согласно выражению i(p)= φ(p)/Z(p), получим соотношение

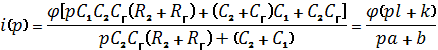. (17)

В выражение (17) введены обозначения:

;

;

;

.

В целях преобразования операционного тока в область оригиналов целесообразно привести выражение (17) к следующему виду

(18)

где ; ; ; .

Коэффициент , найденный описанным нами ранее способом, равен:

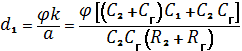
С помощью таблиц обратного преобразования Лапласа [5] для тока находим следующее выражение

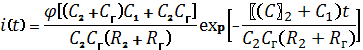. (19)

На рис. 6 представлен график зависимости тока заряжения границы блокированный электрод/твердый электролит от времени, построенный в соответствии с уравнением (19) при следующих удельных значениях параметров:

; ; ; ;

; .

На рис. 7 эта же кривая построена в полном соответствии с уравнением (19) в координатах . Как видно из рис. 7, для всей области исследованных времен кривая заряжения подчиняется уравнению заряжения классической R-C цепочки.

Заключение

Проведенный нами в настоящей работе сравнительный анализ показывает, что кинетические соотношения ток – время для процесса формирования двойного электрического слоя на границе блокированный (инертный) электрод/твердый электролит в хронопотенциометрическом режиме функционально отличаются друг от друга в случае малых времен, с одной стороны, и больших времен заряжения – с другой. Данное утверждение справедливо для всех типов электродов, т.е. кинетические соотношения ток – время не зависят от геометрических особенностей применяемых в электрохимических системах электродов (плоского, цилиндрического или сферического).

В хроноаперометрическом режиме заряжение границы блокированный электрод / твердый электролит гораздо быстрее происходит при больших временах (схема Джекобсена – Веста), чем в случае малых времен (схема Графова – Укше).

Что касается возможности применения эквивалентных электрических схем в релаксационных методах, то она была доказана и ранее другими исследователями [9,10]. Единственным требованием при этом является наличие линейной связи между возмущением и откликом (реакцией) системы [2].

В нашу задачу не входил анализ поведения рассматриваемой границы при очень больших временах (область низких и инфранизких частот), когда в эквивалентной электрической схеме появляется элемент с постоянным сдвигом фаз (ПСФ). Поведение элемента с ПСФ в импульсном гальваностатическом режиме было исследовано в работе [11].

СПИСОК ЛИТЕРАТУРЫ

1. Укше Е.А., Букун Н.Г. Твердые электролиты. М.: Наука, 1977. -175 с.

2. Гусейнов Р.М. Релаксационные процессы в твердых электролитах. М.: Наука, 1993. -160 с.

3. Гусейнов Р.М., Раджабов Р.А. // Электрохимия, 2013. т. 49, №10. С.1053-1059

4. Деч Г. Руководство к практическому применению преобразования Лапласа. М.: Наука, 1965. -287с.

5. Справочник по специальным функциям. / Под редакцией Абрамовица М., Стиган И. М.: Наука, 1979. С.809 – 810.

6. Янке Е., Эмде Ф., Леш Ф. Специальные функции. М.: Наука, 1977. С.52.

7. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1973. С.579, 738.

8. Jacobsen T., West K. Diffusion impedance in planar, cylindrical and spherical Symmetry. // Electrochimica Acta. 1995. v.40, № 2. P. 255 - 262.

9. Pilla A.A. // J. Electrochem. Soc. 1970. v.117, №4. P. 467.

10. Levart E., Schuhmann D. // J. Electroanal. Chem. 1971. v.31, №1. P. 129.

11. Гусейнов Р.М. // Электрохимия, 1990. т.26, №6. С. 795-797.

Подписи к рисункам статьи Р.М.Гусейнова и Р.А.Раджабова «Граница блокированный (инертный) электрод / твердый электролит в хроноамперометрическом и хронопотенциометрическом режимах заряжения».

Рис.1. Эквивалентная электрическая схема ячейки с границей блокированный (инертный) электрод / твердый электролит в случае малых времен (пояснения к схеме в тексте статьи).

Рис.2.График зависимости потенциал – время, построенный в соответствии с уравнением (6), при следующих значениях параметров эквивалентной электрической схемы (кривая 1):

S_эл = 1см²; С₁ =210^-6 Ф/см²; С₂=40 10^-6 10^-6 Ф/см²; R₂ =0,08 Oмсм²;

W₂ =160 Oм см²/с^1/2; i = 1 10^-6 A/см²; d₁ = 0,0238 В/с; d₂ = 0,72510^-6 B.

Кривая 2 на рис.2 построена в соответствии с уравнением (16) при следующих значениях параметров:

S_эл=1см²; С₁ =2 10^-6 Ф/см²; С₂ =4010^-6 Ф/см²; R₂ =0,08 Oмсм²;

R_г=2 Oмсм²; С_г =1010^-6 Ф/см²; i = 10^-6 A/ см²; d₁ = 0,084 В/с;

d₂ =1,384510^-3 мВ; d₃ = - d₂ = -1,384510³ c^-1; .

Рис.3.График зависимости тока заряжения границы блокированный электрод / твердый электролит от времени, построенный в соответствии с уравнением (12), при следующих значениях удельных параметров:

; ; ; ;

; .

Рис.4. График зависимости тока заряжения границы блокированный электрод / твердый электролит от времени, построенный в соответствии с уравнением (12) в координатах , при тех же значениях параметров , что и на рисунке 3.

Рис.5.Эквивалентная электрическая схема ячейки с границей блокированный (инертный) электрод / твердый электролит в случае больших времен и всех трех типов электродов (плоского, цилиндрического и сферического): R_г и С_г - сопротивление и емкость, обусловленные геометрией электродов.

Рис.6. График зависимости тока заряжения границы блокированный (инертный) электрод / твердый электролит от времени, построенный в соответствии с уравнением (19) при следующих значениях удельных параметров:

; ; ; ; ;

Рис.7.График зависимости тока заряжения границы блокированный электрод / твердый электролит от времени, построенный в соответствии с уравнением (19) в координатах , при тех же значениях параметров эквивалентной электрической схемы, что и на рис.6.

251659264251660288

Рис. 1.

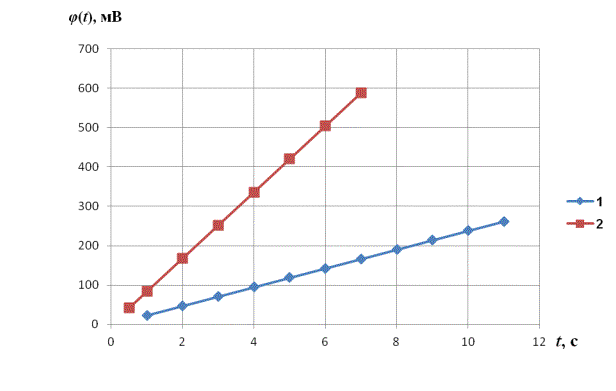
Рис.2.

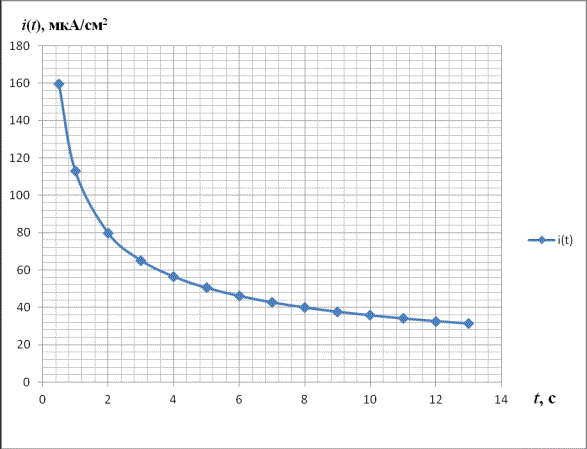
Рис.3.

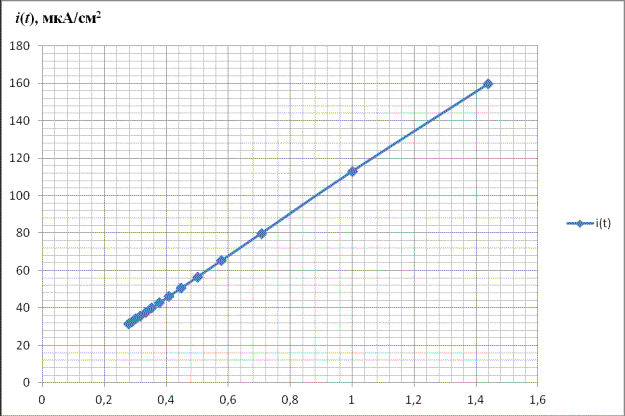
Рис.4.

Рис.5.

0

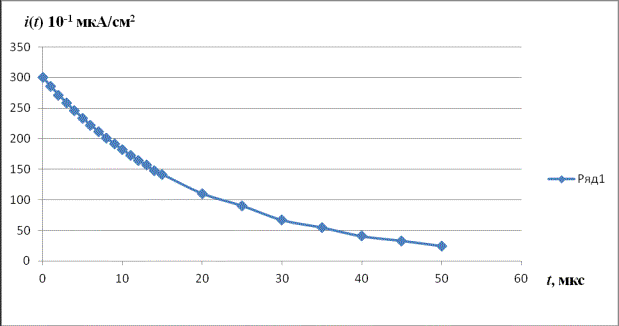
Рис.6.

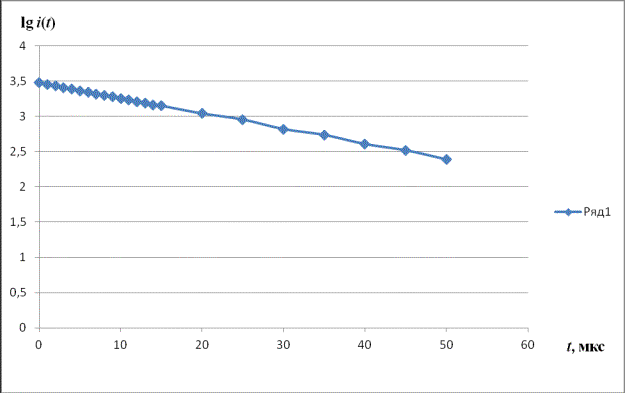
Рис.7.

УДК.135.4

Граница блокированный (инертный) электрод / твердый электролит в хроноамперометрическом и хронопотенциометрическом режимах заряжения

Гусейнов Р.М., Раджабов Р.А.

ЭЛЕКТРОХИМИЯ

Методом операционного импеданса в двух режимах (хроноамперометрическом и хронопотенциометрическом) исследована кинетика процесса заряжения границы блокированный (инертный) электрод / твердый электролит для всех трех типов электродов (плоского, цилиндрического и сферического) в случае малых и больших времен заряжения.

Анализируется случай замедленной диффузии и адсорбции – десорбции одного сорта частиц – дефектов жесткой подрешетки твердого электролита (неосновных носителей тока).

Ил.7. Библиогр.: 11 назв.

[Дагестанский государственный педагогический университет]

Сведения

об авторах статьи «Граница блокированный (инертный) электрод / твердый электролит в хроноамперометрическом и хронопотенциометрическом режимах заряжения».

Гусейнов Ризван Меджидович,

доктор химических наук, профессор Даггоспедуниверситета;

Тел.: 8-928-502-24-02;

E-mail: rizvanguseynov@mail.ru

Раджабов Раджаб Абдулганиевич,

старший преподаватель кафедры информационных и коммуникационных технологий Даггоспедуниверситета;

E-mail: radjab67@mail.ru

Отправляем Вам исправленный и дополненный в соответствии с замечаниями и рекомендациями рецензента вариант статьи Р.М. Гусейнова и Р.А. Раджабова «Граница блокированный (инертный) электрод / твердый электролит в хроноамперометрическом и хронопотенциометрическом режимах заряжения».

С глубоким уважением авторы.

ftse@mail.ru