УДК 519.866

Мошенська А.В.

(аспірант кафедри вищої математики ДВНЗ "КНЕУ імені Вадима Гетьмана")

Методика аналітичного вирівнювання часового ряду для функції рекламної активності

Припустимо, що середня швидкість функції рекламної активності a(t) за часом обернено пропорційна потенційній складовій функції рекламної активності при встановленому максимальному значенні amax підприємства з коефіцієнтом пропорційності A - оцінювання рівня рекламної активності підприємства.

Таким чином, маємо диференціальне рівняння 1-го порядку:

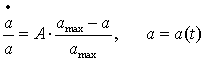, (1)

з початковими умовами, що дозволяють припустити, що в початковий момент часу без заходів по маркетинговому стимулюванню присутня деяка рекламна активність .

Частинний розв’язок диференціального рівняння (1) має вигляд:

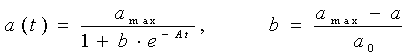. (2)

Якщо значення асимптоти 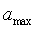невідоме, то спочатку за допомогою регресії оцінюються параметри 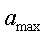і –А рівняння

_{, (3)}

а потім визначають параметр b. Для перетворення логістичної функції визначається різниця між двома оберненими значеннями сусідніх членів часового ряду. Розв’язок має вигляд:

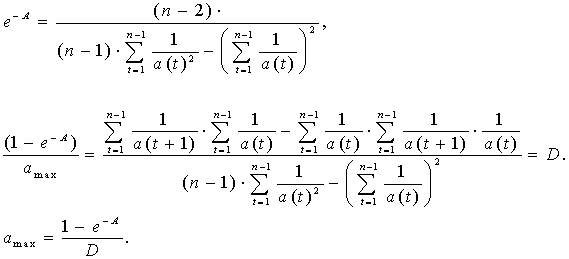
Таким чином, оцінені параметри 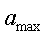і – А рівняння. Для оцінки параметра в, після логарифмування рівняння (2), дістанемо

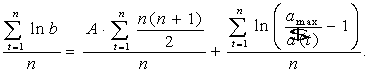
_{Припускаючи, що}

,

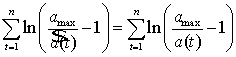одержимо:

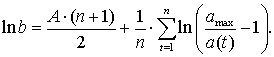(4)

Проведемо аналітичне вирівнювання часового ряду для функції рекламної активності a(t) підприємства, дані часового ряду функції рекламної активності (за період 12 місяців 2013 р.) представлено в табл.1.

Таблиця 1

Часовий ряд функції рекламної активності (тис.грн)

t	1	2	3	4	5	6	7	8	9	10	11	12
	7,62	10,41	12,75	17,18	22	29,61	39,89	47,81	62,5	69,3	87,3	105,3

_{Одержимо значення параметрів:}

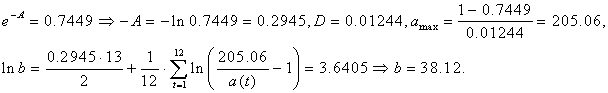
Отже, маємо:

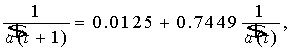
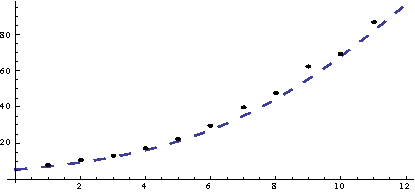
Таким чином, аналітичне вирівнювання часового ряду для функції рекламної активності a(t) підприємства за допомогою логістичної кривої має вигляд (Рис.1):

Отже, приведена методика аналітичного вирівнювання часового ряду для функції рекламної активності a(t) підприємства за допомогою логістичної кривої, якщо не задане значення асимптоти.

Література

1. Потапенко С. Д. Моделювання процесу рекламної діяльності: Автореферат дис. канд. екон. наук: 08.03.02 / С. Д. Потапенко // Київський національний економічний університет. – К., 2004. – 19 с.

2. Лысенко Ю. Г. Эффективное управление рекламным бизнесом / Лысенко Ю. Г., Дынчев С. В., Гнатушенко В. В., Челахов С. В., Демьянов В.М.; Под ред. Ю. Г. Лысенко. – Донецк: ДонНу, 2003. – 228 с.