Современные информационные технологии/2. Вычислительная техника и программирование

Бирликкызы Гулнур

Магистрант информационных технологии в Международном Университете Информационных технологии, г.Алматы, Казахстан

БИНАРНЫЕ И КРАСНО – ЧЕРНЫЕ ДЕРЕВЬЯ. ВРЕМЯ ПОИСКА.

В наше время, время компьютеризации, мы, программисты, часто встречаемся с объектами разного типа в больших объемах; будь то числа, строки, массивы и др. При работе с такими данными сталкиваемся с проблемой сортировки этих данных и поиском среди них. Для того, чтобы иметь возможность быстро вставлять и извлекать объекты и из этого списка, идеальной структрурой данных будет дерево – map (обычно говорят и дерево – карта).

Большинство языков программирования обеспечивают встроенную поддержку для работы с деревьями – map, например класы Java TreeSet/TreeMap, а так же стандартные шаблонные библиотеки для работы с наборами (set) в С++, но из – за совместного пользования, довольно не легко понять, как же все таки работают эти команды.

Для начала рассмотрим общие понятия, используемые при работе с деревьями, а так же термины. Так же рассмотрим для сравнения бинарные деревья поиска, которые хоть и являются идеально отсортированными, но все же не обеспечивают эффективный поиск и вставку новых элементов. И, конечно же, рассмотрим красно – черные деревья, являющихся разновидностью бинарных деревьев поиска.

Дерево представляет собой структуру данных, которое представляет данные в виде иерархии. Оно связывает каждый объект к узлу в дереве и поддерживает отношения родитель/потомок между этими узлами. У любого дерева должен быть узел, обозначаемый корнем, который не является ни чьим потомком, и является начальным узлом, в другом конце дерева содержаться конечные узлы дерева. Максимальная глубина любого узла в дереве называется высотой.

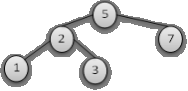
Бинарное дерево – это дерево с одним дополнительным ограничением – элементы в дереве хранятся в определенном порядке. Формально, каждый узел в бинарном дереве поиска имеет два поддерева, если таковых нет, считается узел нулевым. Все элементы в левом поддереве меньше корня, и соответственно, корень меньше элементов в правом поддереве (рисунок 1).

Рисунок 1. Бинарное дерево поиска

Для использовании наборов и карт достаточно сделать обход элементов по порядку. Обход производимый в бинарных деревьях поиска слева направо известны как симметричный обход дерева. В дереве, где у каждого узла имеется значение и два указателя на левый и правый поддеревья, симметричный обход можно сделать следующим образом:

Procedure simmetr_travers(Node n)

if(n == nil) return;

simmetr_travers (n.left_subtree);

Print(n.value);

simmetr_travers (n.right_subtree);

…

simmetr_travers (root);

При добавлении нового узла в дерево двоичного поиска, новый узел всегда будет листом в дереве, и для вставки необходимо ориентироваться на корень дерева. Если новое значение узла меньше, чем текущее значение узла, то идем влево – если оно больше, то идем прямо. Достигая крайний листовой узел, прикрепляем узел к левому краю листа.

Рассмотрим пример, где нужно вставить узел со значением = 4 в БДП, на рисунке 1. Для этого надо сделать следующие шаги:

1. Пусть корень = 5 является текущим узлом

2. Поскольку новый узел меньше текущего узла, мы пойдем на лево, и устанавливаем в качестве текущего узла

3. Теперь новый узел больше текущего узла, идем прямо на правую сторону, текущий узел =3

4. Итак, достигаем листа, и прикрепляем новый узел по правую сторону листа. Дерево будет выглядеть следующим образом:

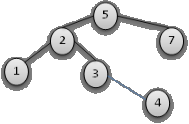
В общем, имеется 3 случая, для удаления узла n из бинарного дерева поиска.

1. Если у n нет потомков, то удаляем n из дерева (рисунок 2)

2. Если у n есть одно поддерево, мы удаляем n и соединяем поддерево n с родителем n (рисунок 3).

3. Если у n есть 2 поддерева, то выполняем следующие шаги (рисунок 4):

a) Находим наименьший узел, который был бы больше n, назовем его m;

b) Удаляем m из дерева;

c) Заменяем n значением m.

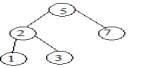
Рисунок 2. Удаление узла. Способ 1

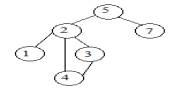
Рисунок 3. Удаление узла. Способ 2

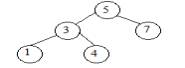
Рисунок 4. Удаление узла. Способ 3

При поиске определенного элемента в бинарном дереве поиска мы пользуемся элементарной навигацией, то есть, начиная от корня дерева идем налево, если текущий элемент узла больше, чем ищем, в противном случае, идем направо. При любом раскладе время работы поиска элемента в дереве выполняется за O(h), где h – высота дерева. Из вышеизложенного можно сделать вывод, что при худшем случае добавления элементов в дерево, оно может выглядеть как связанный список, в этом случае время поиска элемента будет O(N), где N – число узлов в дереве.

Во избежание таковой проблемы рассмотрим красно – черное дерево.

Красно - черные деревья являются модифицированным видом бинарных деревьев, которые могут сохранить сбалансированность, при этом, не влияя на сложность примитивных операции. Происходит это путем окрашивания каждого узла в красный или черный цвет, при этом сохраняя набор свойств, гарантирующие, самый глубокий путь в дереве не больше чем удвоенный самый короткий.

Красно – черное дерево это бинарное дерево поиска обладающий свойствами:

a) Каждый узел имеет цвет либо красный. Либо черный

b) Все листья (нулевые узлы) окрашены в черный цвет

c) Оба потомка каждого красного узла — черные.

d) Всякий простой путь от данного узла до любого листового узла, являющегося его потомком, содержит одинаковое число черных узлов. [3]

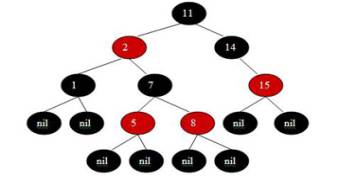
Рисунок 5. Красно – черное дерево

Вставка элементов в красно – черное дерево состоит из двух этапов:

1. Обычная вставка элемента как в бинарном дереве поиска

2. Фиксация нарушении во время добавления нового элемента, повторное окрашивание некоторых узлов.

То есть, общее время работы процесса является O(log n). На рисунке 6 показано дерево до и после вставки элемента со значением «4»

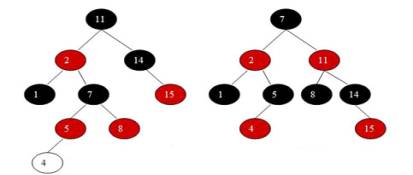
Рисунок 6. Вставка узла в красно –черное дерево

При удалении делаются те же самые действия, что и при добавлении нового элемента. И так общее время работы для процесса удаления занимает O(log N) время, что отвечает требованиям сложности для примитивных операции.

Итак, в ходе работы было выявлено, что если работать с заранее отсортированными данными, то есть входные данные уже расположены по порядку, то скорость работы бинарных деревьев поиска гораздо быстрее нежели скорость красно черных деревьев, но так же было выявлено, что при удалении и добавлении элементов в начальный массив данных, благодаря вращательным операциям красно черных деревьев, с ними работать гораздо проще.

Список литературы:

1. A. Michael Berman Data Structures via C++: Objects by Evolution OUP: USA 1997, - 496 p.

2. E.Horowitz, S.Sahni, D.P. Mehta Fundamentals in Data Structures in C++, Second Edition, Silicon Pr 2006 – 694 p

3. https://class.coursera.org/algo-004/lecture/76 (дата обращения: 20.04.2014 )