Абатов Н.Т., кандидат физико-математических наук, доцент Костанайского государственного университета им. А.Байтурсынова г.Костанай, Казахстан

Методы решения некоторых тригонометрических неравенств

Выпускники школ затрудняются при решении сложных тригонометрических неравенств, которые часто встречаются на ЕНТ по математике. Поэтому рассмотрим некоторые сложные тригонометрические неравенства и укажем способы их решения.

Задача №1. Решите неравенство:

Решение. Применяем формулу Тогда

уравнение примет вид: 2(1-

.

Введём замену: y. И получаем квадратное неравенство:

.

Применяем метод интервалов. Находим корни квадратного трехчлена:

Тогда множество является решением квадратного неравенства .

Производим обратную замену y. Тогда имеем: .

Это двойное неравенство равносильно неравенству так как областью допустимых значений функции y является множество

Итак, решаем неравенство

Ответ: [.

Задача №2. Решите неравенство:

Решение. Применяем формулу:

Тогда имеем:

Введём замену: Тогда получаем квадратное неравенство: Применяем метод интервалов. Тогда множество является решением неравенства

Производим обратную замену: Тогда имеем: .

Решением этого двойного тригонометрического неравенства является совокупность двух неравенств вида:

Преобразуем полученные неравенства:
.

Ответ: [ .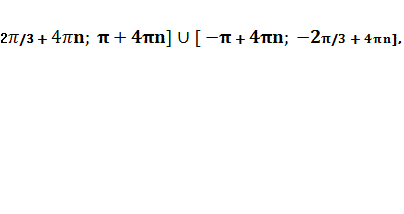

Задача №3. Решите неравенство:

Решение. Применяем формулу двойного угла:

Тогда данное неравенство примет вид:

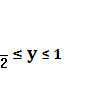Введём замену: Тогда имеем: Применяем метод интервалов. Тогда множество является решением неравенства

Производим обратную замену: Тогда имеем: .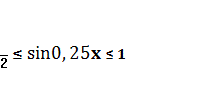

Это двойное неравенство равносильно неравенству: так как областью допустимых значений функции y является множество

Итак, решаем неравенство

Ответ: [ .

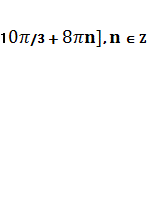Задача №4. Решите неравенство:

Решение. Применяем формулу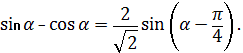

Тогда имеем:

Учтём, что функция положительная в первой и во второй четвертях. Поэтому неравенство имеет решение:

Ответ:

Задача №5. Решите неравенство:

Решение. Обе части данного неравенства умножим на и применяем формулу

Тогда имеем: ;

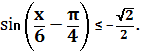
Находим решение полученного неравенства:

Итак, множество [ является решением исходного неравенства.

Ответ: [

Литература

1. Абатов Н.Т. Методы решения задач по математике. Алгебра. Учебное пособие для поступающих в ВУЗы.- Костанай, 1998г.

2. Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике. Справочное пособие.-Москва,1995г.