Математика/ 2. Перспективы информационных систем

Тимощук А. С.

Донской Государственный Технический Университет, Россия

Реализация процесса расчета символа ядра интегрального уравнения в приложении для сервера баз данных

В работе представлена реализация процесса расчета символа ядра интегрального уравнения в приложении для сервера баз данных.

В качестве примера рассматривается задача кручения бесконечного неоднородного цилиндра с помощью жесткого бандажа.

Данная задача сводится к решению парного интегрального уравнения первого рода. Решается данное уравнение полуаналитическим методом. В частности, образование ядра интегрального уравнения – есть решение дифференциального уравнения второго порядка с переменными коэффициентами. Решение строится численным методом (задача Коши). Построенный образ ядра аппроксимируется специальным аналитическим выражением в виде дробно-рациональной функции. Для данной функции находится решение интегрального уравнения в явном виде.

В работе обоснован выбор инструментов для реализации расчета, а также расчет прошел на тестовом примере однородной среды.

1. Постановка задачи

Рассматривается задача кручения бесконечного неоднородного цилиндра радиуса R с помощью ограниченного жесткого бандажа.

Модуль сдвига — гладкая функция радиуса:

G = G(r), 0 ≤ r ≤ R (1)

M — крутящий момент, приложенный к бандажу. Его ось совпадает с осью цилиндра — z. Бандаж контактирует с цилиндром в области размером 2a.

Под действием момента М бандаж повернется относительно оси z на угол θ, тем самым вызовет деформацию кручения цилиндра. Сделаем предположение, что бандаж плотно прилегает к цилиндру и между ними отсутствуют силы трения. Схема кручения изображена на рисунке 1.

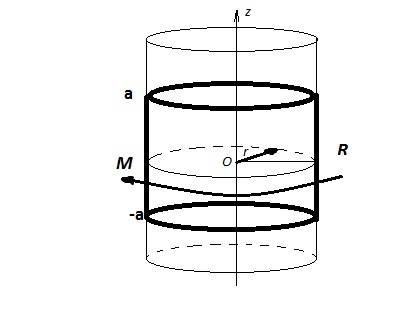
Рис.1

В таком случае граничные условия будут иметь вид:

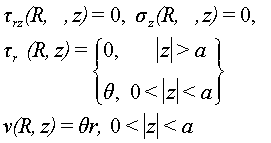(2)

ν(r, φ, z) – угловое перемещение, – касательные напряжения, нормальные напряжения , и отсутствуют.

При r = 0 напряжения ограничены, при - исчезают.

Требуется определить распределение контактных касательных напряжений под бандажом

(3)

и связь между крутящим моментом М и углом θ, согласно формуле (F – круг радиуса R):

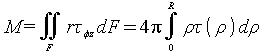
2. Решение уравнения

Символ ядра интегрального уравнения, согласно разработанному ранее методу, можно построить по формуле

(16)

, где - функция Макдональда,

а - определяется из задачи Коши.

Три первых граничных условия (2) исходной контактной задачи для цилиндрической шахты удовлетворены в ходе решения вспомогательной задачи. Так же удовлетворены условия при и при .

3. Инфологическая модель

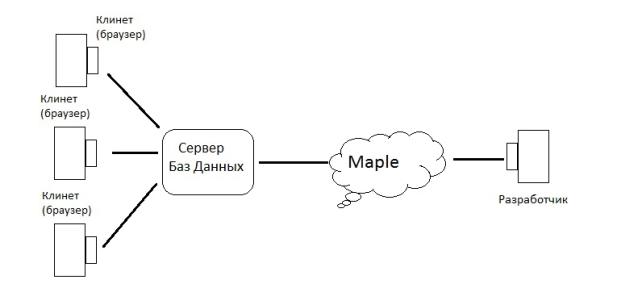
Схема включает в себя работу с информационной системой. Каждый субъект имеет свои права доступа к информационным задачам системы.

В браузер клиента в виде изображений выводятся значения контактных напряжений и деформаций внутри цилиндра, сохраненные в Базе Данных в виде таблиц и рассчитанные разработчиком в математическом пакете Maple.

4. Программная реализация рассчета

Решение задачи представляет собой 2 подпрограммы. В первой части реализуется решение задачи Коши, заданы начальные условия. Решение системы ОДУ записывается в специальный файл с расширением .m, в виде процедуры, для дальнейшего использования при построении трансформанты. Здесь также указаны модифицированные функции Бесселя, необходимые для расчета. В математическом пакете Maple данные функции имеются в библиотеке, что облегчает код программы, не загромождая большими формулами и облегчает построение решения.

Вторая часть содержит вызов ранее описанной процедуры решения задачи Коши, а также построение законов неоднородности и трансформанты ядра.

5. Реализация в приложении для сервера баз данных

При запуске USBWebServer с носителя, автоматически открывается главная страница, на которой представлено краткое описание контактной задачи. Под изображением схемы деформирования упругого неоднородного цилиндра находится ссылка «Графические иллюстрации решения задачи», где расположены результаты решения задачи. Главная страница представлена на рисунке 2

Рис 2. Главная страница

Результатом решения задачи является построение трансформанты ядра. На рисунке 3 представлено численное построение трансформанты ядра интегрального уравнения, в обычной системе координат и в логарифмической шкале.

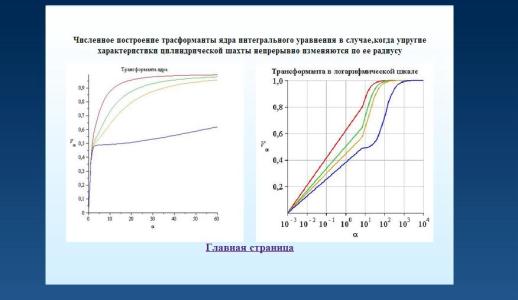
Рисунок 3. Построение трансформанты ядра

Практическим результатом работы будет являться информационная система поддержки принятия решения в ходе реализации аналитических методов определения напряженно-деформированного состояния неоднородного цилиндра.

Возможно дальнейшее развитие в следующих направлениях:

· Применение структур и алгоритмов для расчётов с произвольной точностью.

· Реализация расчёта других специальных функций, имеющих прикладное значение.

· Подключение базы данных для хранения результатов расчётов и повторного их использования с целью ускорения вычислений.