Математика/5. Математическое моделирование

УДК 681.32

Сведения об авторе статьи: Евсеев Владислав Иванович, кандидат физико-математических наук, доцент, кафедра прикладной информатики Казанского (Приволжского) федерального университета.

Information about the contributor: Yevsey Vladislav Ivanoviches, Candidate of Physics and Mathematical Sciences, docent, the department of the applied information theory of Kazan' (Volga) federal university.

В.И. Евсеев

Казанский (Приволжский) федеральный университет, Казань, Россия,

кафедра прикладной информатики

1 - vladislaw.evseev@yandex.ru, 89047610772

Аннотация:

В данной заметке изучаются возможности применения матричных методов к многослойным (тернарным и квадратичным) операциям, а также композиционные представления и критерии (условия) разложимости многослойных операций.

О МАТРИЧНЫХ ФОРМАХ МНОГОСЛОЙНЫХ ОПЕРАЦИЙ

§ 1. ТЕРНАРНЫЕ ОПЕРАЦИИ

Тернарные операции являются обобщением бинарных операций на случай, когда заданы три исходных высказывания: X,Y, Z.

Для них строится последовательность бинарных операций, которая называется композицией, то есть, тернарная операция является композиций бинарных операций. При этом одна из бинарных операций, которая выполняется первой, называется внутренней, а вторая – внешней. Символически можно обозначить внутреннюю бинарную операцию символом “ ”, а внешнюю – символом “□”или “◊”.

Так как последовательность выполнения двух бинарных операций может быть различной, то можно рассмотреть два вида схем тернарных операций:

а) первой выполняется внутренняя композиция

(1.1)

а затем – внешняя операция

. (1.2)

Результатом является тернарная операция

(1.3)

б) внутренняя бинарная операция выполняется второй,

в этом случае

. (1.4)

Эту операцию удобно представить в виде композиции, если положить для внутренней бинарной операции:

(125)

Тогда получаем:

(1.6)

Для построения таблиц истинности тернарных операций также будем использовать матричный метод, который основан на применении матриц Карно. При этом сначала каждая внутренняя бинарная операция записывается в виде рабочих блоков, затем также записывается внешняя бинарная операция, а после первый результат подставляется в полученное выражение и вычисляется окончательный вид рабочих блоков символьного массива. В таблицах Карно обычно крайним считается высказывание, характеризующее внешнюю операцию. Однако при построении сравнительных таблиц высказывания расставляются по договоренности, чтобы иметь возможность сравнивать результаты.

Рассмотрим схемы для обоих видов тернарных операций, а затем приведём некоторые наиболее существенные для дальнейшего изложения примеры.

а) Если первой выполняется внутренняя бинарная операция

то её матрица истинности может быть записана в виде:

Y X	0	1
0
1

Поэтому символьный массив записывается через рабочие блоки:

(1.7)

Для внешней бинарной операции получаем соответствующую таблицу истинности:

Z M	0	1
0
1

Значит, для внешней бинарной операции получаем формулу рабочих блоков:

(1..8)

Предварительно вычисляем значение :

(1.9)

Теперь выражения из формул (7.7) и (7.9) подставляем в формулу для внешней операции и находим окончательное выражение для всей тернарной операции. Символьный массив для тернарных операций первого типа может быть записан в виде таблицы:

Q ( 1 тип )

На основе символьного массива строится совокупность рабочих блоков тернарной операции первого типа. В дальнейшем мы будем опускать символ конъюнкции и записывать выражения в виде стандартного произведения.

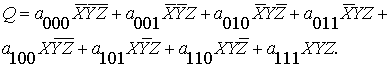(1.10)

В этой формуле приняты обозначения:

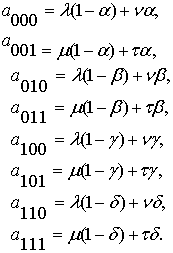(1.11)

Значит, матрица функции истинности по схеме Карно может быть записана в виде:

Z	Y X	0	1
0	0
0	1
1	0
1	1

Аналогично получаются результаты и для второго вида тернарных операций. Этот случай может быть записан в виде:

(1.12)

где

. Иногда рассматриваются так называемые «обратные задачи», когда исходно определена только таблица истинности (в традиционных случаях – это линейная таблица), и по указанным в ней значениям функции истинности предлагается построить вид самой тернарной операции. При этом тернарная операция имеет таблицу:

n	0	1	2	3	4	5	6	7
X	0	0	0	1	1	1	1	1
Y	0	0	1	0	0	0	1	1
Z	0	1	0	0	0	1	0	1
Q	a	b	c	d	e	f	g	h

Сначала мы рекомендуем построить поле Канта по заданным значениям рабочих блоков, а затем записать выражение для совокупности рабочих блоков и функцию истинности этой операции.

Примечание. Произвольная тернарная операция, заданная линейной таблицей, может не быть представима в виде композиции бинарных операций. Такие тернарные операции составляют третий тип. Условие представления тернарной операции в виде композиции бинарных операций имеет вид определителя, составленного из коэффициентов значений операции в линейной таблице:

(1.13)

Этот критерий позволяет выделить третий тип тернарных операций и проверить возможность представления произвольно заданной тернарной операции в виде композиции бинарных операций. Полное доказательство этого критерия будет приведено далее.

§ 2. КВАДРАТИЧНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ.

Квадратичные логические операции (сокращенно «квадра-операции») могут быть нескольких типов: дважды бинарные и цепочные последовательности (четырех типов). Кратко рассмотрим их строение и методы вычисления.

Отметим, что мы всюду применяем матричные виды таблиц истинности, которые удачно раскрывают структуру этих операций. В общем случае матрица значений функции истинности для квадра – операции имеет вид

T		0	0	1	1
Z	Y X	0	1	0	1
0	0
0	1
1	0
1	1

Для каждого типичного случая таких операций матричная форма таблицы истинности конкретизируется с учётом реального вида формулы. Значения параметров операции принадлежат множеству {0;1}. Существует множество типов квадра – операций.

Рассмотрим основные из них.

Дважды бинарные логические операции.

Они содержат две внутренние бинарные операции, связанные одной внешней логической операцией, поэтому выражаются формулой:

(2.1)

Каждую часть следует сначала рассмотреть отдельно как бинарную операцию, затем, также отдельно, построить внешнюю бинарную операцию, и лишь после этого соединить все результаты в одну формулу. Рассмотрим сначала первую внутреннюю бинарную операцию:

(2.2).

Для неё получаем таблицу истинности:

Y X	0	1
0
1

и формулу рабочих блоков:

(2.3)

Для взаимной к ней операции получим:

(2.4)

Аналогично строится и вторая внутренняя бинарная операция:

Для неё мы тоже запишем таблицу истинности

T Z	0	1
0
1

и формулу рабочих блоков:

.

(2.5)

Для взаимной к ней операции получаем формулу:

. (2.6)

Теперь строим внешнюю бинарную операцию:

Для этой операции также строим свою таблицу истинности

N M	0	1
0
1

и формулу рабочих блоков:

(2.7).

Обозначим выражения логических блоков квадра – операции в виде матрицы Тогда для этой матрицы получаем таблицу:

j i	1	2	3	4
1
2
3
4

Таким образом, символьный массив квадра – операции можно представить в виде

T Q		0	0	1	1
Z	Y X	0	1	0	1
0	0
0	1
1	0
1	1

Значения выражений определяются как произведения соответствующих высказываний или их отрицаний:

=, =, =, =,

=, =, =, =, (2.8)

=, =, =, =,

=, =, =, =.

Кроме этого вида для квадра – операций применяется структура «поля Канта».

Квадра поле Канта

Q
	= =
		0000	0100	0001	0101
		1000	1100	1001	1101
		0010	0110	0011	0111
		1010	1110	1011	1111

Учитывая выражения для матриц истинности внутренних операций, получим значения матрицы истинности внешней бинарной операции, которую будем структурировать аналогично с приведённым выше символьным массивом. При этом следует учитывать, что при внешнем отрицании во внутренних операциях изменяется сам вид матриц истинности.

Таким образом, теперь мы находим явный вид матрицы истинности квадра – операции, как алгебраической структуры, соответствующей полю Канта (для рабочих блоков значения матрицы истинности равны 1, а для нерабочих они равны 0).

Примечание:

в конкретных задачах изображение поля Канта упрощается, так как четырёхзначные шифры блоков не пишутся.

Матрица определяется через значения матриц истинности двух внутренних и одной внешней бинарных операций:

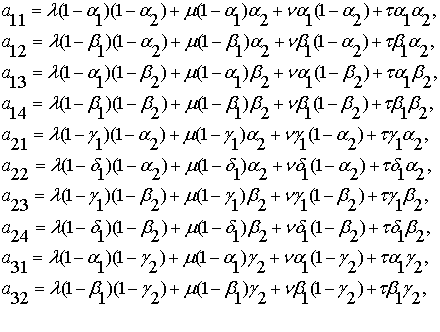(2.9)

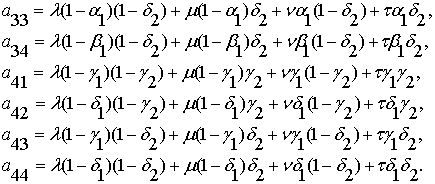
«Цепочные» квадратичные операции.

Существует четыре различных по смыслу случая «цепочных» квадратичных операций:

а) каждое последующее высказывание, кроме первых двух, объединённых внутренней бинарной операцией, является внешним по отношению к предыдущей формуле:

(2.10)

б) два внутренних высказывания объединены в одну операцию, а последнее высказывание является внешним:

(2.11)

в) первое высказывание является внешним, а второе и третье объединены в одну операцию:

(2.12)

г) Первое высказывание является внешним, а внутренняя бинарная операция объединяет два последних высказывания:

(2.13)

Рассмотрим подробно первую из этих формул, а остальные схемы аналогичны.

Итак, пусть известна «цепочная» квадра – операция первого вида.

Для неё получаем последовательность «вложенных» бинарных операций:

Каждую из этих операций анализируем как бинарную.

Мы не будем записывать стандартные виды структуры четырех блоков каждой операции, а сразу укажем виды рабочих блоков заданной и взаимной бинарных операций.

Для первой бинарной операции в этой цепочке получаем:

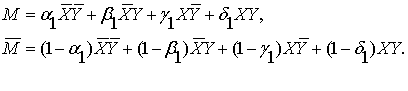(2.14)

Аналогично находим для второй операции этой цепочки:

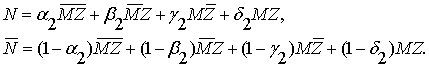(2.15)

Третья операция этой цепочки является финальной и рассматривается условно как внешняя. Для неё получаем исходное выражение:

(2.16)

Промежуточную операцию (N) проанализируем как тернарную операцию первого типа:

(2.17)

Для неё получаем таблицу матрицы истинности:

Z	Y X	0	1
0 0	0
	1
1	0
	1

Аналогично строится таблица истинности для отрицания промежуточной операции (), из которой затем конструируется выражение для всех операции Q. Мы приведём только вид матрицы для отрицания промежуточной операции, а окончательную формулу можно записать в виде значений матрицы истинности всей цепочной квадратичной операции. Взаимная к формуле (14.17) операция имеет матрицу истинности:

Z	Y X	0	1
0 0	0
	1
1	0
	1

Аналогично могут быть проанализированы и другие виды «цепочных» квадратичных операций.

§ 3. ПРЕДСТАВЛЕНИЯ ТЕРНАРНЫХ ОПЕРАЦИЙ

Прежде всего, дадим доказательство уже указанного в первом параграфе критерия представления тернарной операции в виде композиции бинарной и унарной операций. Для этого введем упрощенные обозначения параметров тернарной операции двух видов:

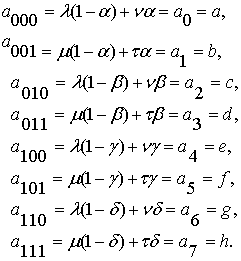(3.1)

Теперь определитель второго порядка для разложимости этой тернарной операции можно представить в двух эквивалентных формах:

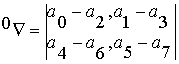(3.2)

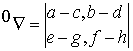(3.3)

Отдадим предпочтение формуле (3.2), и условие разложимости представим в виде:

(3.4)

Раскрывая этот определитель, получаем условие

(3.5)

Здесь введены обозначения:

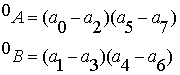(3.6)

Вычислим эти выражения с помощью формул (1.11).

Для первого значения получаем:

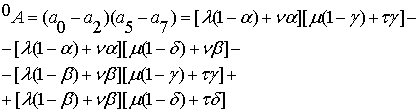(3.7)

После небольших вычислительных преобразований находим:

(3.8)

Аналогично, для второго выражения найдем:

(3.9)

После преобразований получаем:

(3.10)

Равенство этих выражений и показывает справедливость указанного критерия разложимости тернарной операции.

Позволим себе привести один пример. Одна из симметричных тернарных операций имеет вид:

(3.11)

Проверим для нее выполнение критерия разложимости и найдем сам результат. Здесь отличные от нуля параметры операции равны:

. (3.12)

По установленному критерию вычисляем определитель:

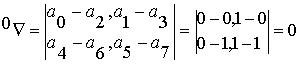(3.13)

При этом легко показать, что реальный вид этой операции представляет собой композицию внутренней и внешней эквиваленций:

(3.14)

Аналогично, можно найти критерий разложимости кадра-операции, этот критерий имеет вполне естественный вид:

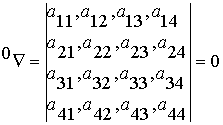. (3.15)

Отметим, что этот критерий также доказывается с помощью формул (2.9), но представляет собой большие вычислительные трудности, так как вычисление этого определителя приводит к построению однородной формы четвертого порядка, основными переменными в которой являются параметры внешней бинарной операции, а параметры внутренних бинарных операций оказываются также внутренними параметрами для самой этой формы. Мы не будем рассматривать это доказательство, хотя в монографии его можно было бы и привести.

ЛИТЕРАТУРА:

1.Ю.Л.Ершов, Е.А.Палютин. Математическая логика. СПб.«Лань».2005.

2. В.И.Евсеев. Логика. Изд – во ТАРИ. Казань. 2001.