Математика/5Математическое моделирование

                            к.ф.-м.н. доц.  В.И. Евсеев  

Казанский  (Приволжский) федеральный университет, Казань, Россия  кафедра прикладной информатики

   УДК 681.32                        1 - vladislaw.evseev@yandex.ru, т.89047610772

 

О МЕТОДАХ   ЛОГИЧЕСКОГО ИНТУИЦИОНИЗМА        

                  

         § 1. ПОСТРОЕНИЕ ФУНКЦИОНАЛЬНОЙ МОДЕЛИ в .                

         1.1. В классической двузначной логике  основными классами истинности являются:

 

                   H – класс ложных высказываний,

                   E – класс истинных высказываний.

 

Для их функциональной характеристики вводится отображение этих классов в двухэлементное множество {0;1} по определению:

 

                  

 

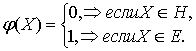
         При этом каждое высказывание может быть записано в функциональном виде:

 

                                                                     (1.1.)

В классической двузначной логике вводятся обозначения:

 

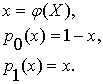                                                                                   (1.2)

 

Для отрицания высказывания Х получаем формулу:

 

                                                                     (1.3)

 

из которой следует, что

 

                                                                                    (1.4)

 

         Особенностью классической двузначной логики является выполнение закона двойного отрицания:

 

                            .                                                             (1.5)

 

1.2.  Для построения бинарных операций рассматриваются два высказывания, заданных в функциональном виде:

 

                                                                     (1.6)

 

Бинарная операция ставит им в соответствие третье высказывание Z, также заданное в функциональной форме:

 

                                                                      (1.7)

 

Для бинарной операции вводится обозначение:

 

                                                                                         

 

Бинарная операция характеризуется значением функции истинности:

 

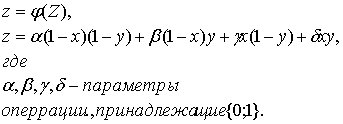                                   (1.8)

Для бинарной операции строятся матрицы арифметической функции истинности и символьного массива, которые затем связываются блочной матрицей всей бинарной операции.

         Матрицы функции истинности и символьного массива таковы:

 

         Y

X

 

     0        

 

      1

   

     0

 

    

 

    

 

      1

 

         

 

      

 

        

    Z

 

             

 

     

   

    

 

    

 

    

 

    

 

        

 

    

 

        

        

 

 

 

 

 

 

 

 

         В логике удобным бывает применение специального умножения этих матриц, которое является обобщением скалярного произведения векторов в аналитической геометрии.

         Для построения «логического» произведения составляется таблица, в которой  строками являются последовательности параметров арифметической матрицы и соответствующих блоков символьного массива.

Затем элементы вертикальных столбцов перемножаются и суммируются, а результатом оказывается формула для функции истинности бинарной операции  (1.8).

         Таблица «логического умножения имеет вид:

 

 

 

 

Z

 

 

 

Здесь через  обозначено декартово произведение универсума высказываний  W  на себя (его логический квадрат).

Теперь для каждой бинарной операции получаем свою структурную формулу, которая затем будет преобразована в функциональную, с помощью введения отделяющих функций логических классов в каждом отдельном случае с учетом специфики построения модели.

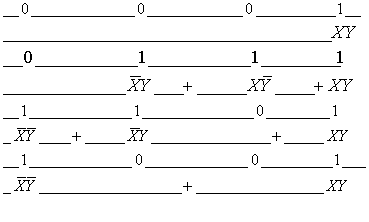
          Таким образом, основные бинарные операции (конъюнкция, дизъюнкция, импликация, эквиваленция) могут быть заданы в виде следующей таблицы:

 

 

 

 

 

 

                  

 

 

 

 

 

 

 

 

 

 

 

 

         Здесь приняты обозначения основных логических операций:

                  

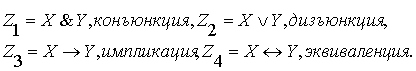
         1.3. Для дальнейшего изложения нам будут необходимы аксиомы и правила вывода, применяемые  при изучении логики.

Аксиомы классической логики проектируют возможности вывода из истинности исходных высказываний их различных композиций:

 

                  

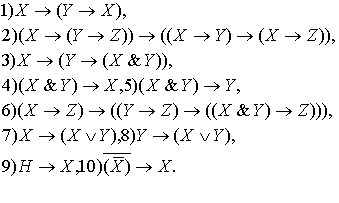
Обратим внимание читателя, что аксиома (10) не эквивалента формуле (1.5), так как по формуле (1.5) получаем:

 

                  

 

 а по аксиоме 10) получаем только нестрогое неравенство:

 

                                                                                  (1.9)

 

Поэтому в классической логике  значение двойного отрицания не превышает значения исходного высказывания.

         Основное правило вывода имеет вид:

 

                                                                                               (1.10)

                  

 

         § 2. ФУНКЦИОНАЛЬНАЯ ИНТЕРПРЕТАЦИЯ

                  ИНТУИЦИОНИСТКОЙ ЛОГИКИ

 

         2.1.  Обобщением классической двузначной логики являются различные варианты логики, развитой на основе интуиционизма как  совокупности математических идей и методов, отрицающих излишне детерминированный подход к построению логических структур.

         Интуиционистская логика была впервые четко сформулирована А. Гейтингом [1],  а затем более глубоко рассмотрена С.Клини [2].

         В данной заметке мы рассмотрим методику построения одной из возможных функциональных моделей подобной логики, в которой будет построена логика первого уровня, или унарная схема.

         Во-первых, введём значения относительных классов лжи и истины, погруженных в основной универсум W, полагая:

а) значения новых классов истинности h,e располагаются в следующем порядке:

 

                                                                                 (2.1)

б) значения функции истинности на новых классах истинности определяются условиями

 

                  

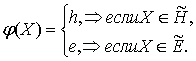
В) классы истинности         характеризуются погружением:

                  

                   

        

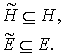
Во-вторых, будем считать функции истинности в исходной формуле (1.1) нелинейными. В данной заметке мы остановимся на параболической модели, полагая квадратичную зависимость:

 

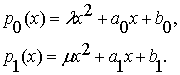                                                                    (2.2)

Здесь - параметры нелинейности определяющих функций классов относительной истинности. Рассматриваемую нами модель интуиционистской логики обозначим  , не уточняя пока её размерность.

         2.2. Рассмотрим сначала случай линейности отделяющих функций, полагая, что параметры нелинейности равны нулю. В этом случае получим по характеризующим свойствам отделяющих функций условия на линейные параметры:

 

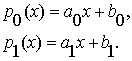                                                                             (2.3)

 

Подставляем в эти формулы значения функции истинности на классах

 и получаем явные выражения для отделяющих функций:

 

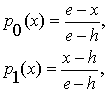                                                                                  (2.4)

 

что указывает на линейность отделяющих функций в этом случае.

         Таким образом, получаем функциональное выражение исходного высказывания через классы относительной истинности:

 

                                                                      (2.5)

        

         Теперь проверим выполнение закона двойного отрицания (1.5) для этого случая. В отличие от классической логики мы будем обозначать отрицание высказывания в логике  символом  , а для двойного отрицания получим:

 

                                                                                (2.6)

 

         В случае линейности отделяющих функций можно записать

 

                            ,                                       (2.7)

 

Поэтому для функции истинности отрицания находим:

 

                            .

 

И после простых вычислений получаем окончательный вид функции истинности отрицания:

 

                                                                         (2.8)

 

Теперь находим для функции истинности двойного отрицания:

 

        

 

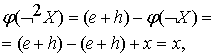
что и является доказательством выполнения закона двойного отрицания.

         2.3. Перейдём теперь к квадратичному заданию отделяющих функций по формулам (2.2). Для функции   запишем граничные условия в виде системы:

 

                  

 

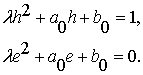
Выразив отсюда значения  через параметр нелинейности , находим:

 

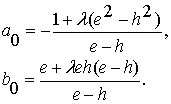
                                                                   (2.9)

 

Значит, сама отделяющая функция имеет вид:

 

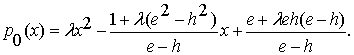                                (2.10)

 

Аналогично находится и отделяющая функция  Для неё получается система граничных условий:

 

                  

 

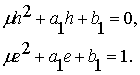
Из этой системы выражаем значения   через параметр :

 

                                                                        (2.11)

 

Так находится вторая отделяющая функция:

 

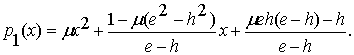                                (2.12)

Если подставить эти функции в формулу для X, то получим функциональное представление общего вида в случае квадратичных отделяющих функций:

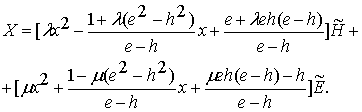                               (2.13)

 

Из этой формулы находим значение самой функции истинности

         ,                                  (2.14)

 

Но по определению    следовательно, должно выполняться условие, связывающее параметры нелинейности:

 

                  

 

Поэтому существует ненулевой параметр , через который выражаются параметры нелинейности:

                                                                                        (2.15)

 

Используя формулы (2.15), найдём окончательный вид для функционального выражения высказывания через отделяющие функции.

Оно получается подстановкой значений параметров нелинейности по формуле (2.15) в формулу (2.13).

          Запишем эту формулу, так как она понадобится нам в дальнейшем:

 

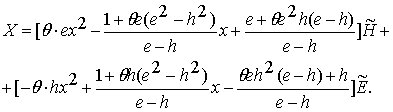                         (2.16)

 

2.4. Теперь укажем  явный вид для отрицания исходного высказывания в логике , с учетом однопараметрического задания.

         При отрицании высказывания Х в формуле (2.16) меняются местами символы классов истинности, поэтому получаем:

        

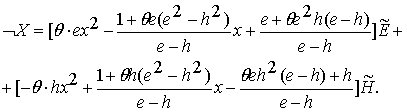                      (2.17)

 

Если для простоты ввести обозначение  , то можно записать выражение для функции истинности отрицания:

 

         .                     (2.18)

 

Таким образом, отрицание для квадратичных отделяющих функций отличается от линейного случая присутствием второго слагаемого, содержащего согласованный параметр нелинейности  .

 

         § 3. ПРОБЛЕМА ДВОЙНОГО ОТРИЦАНИЯ

 

          3.1.Перейдём к вычислению функции истинности для двойного отрицания исходного высказывания, чтобы затем определить возможности выполнения закона двойного отрицания.

         Второе отрицания представим как подстановку в формулу (2.18) значений

                  

 

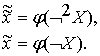
Таким образом, находим:

 

        

Так как из формулы (2.18) получаем

 

  (3.1)

то разность значений до и после двойного отрицания равна:

 

                                     (3.2)

 

Таким образом, при выполнении закона двойного отрицания (1.5) находим два варианта:

 

         а)

         б)  при 

         получаем уравнение

 

                                                               ( 3.3)

 

Отсюда следует:

 

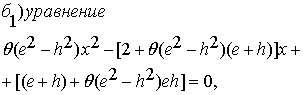                                             (3.4)

        

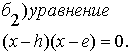                                                                                 (3.5)

 

         Заметим, что дискриминант уравнения (3.4) равен сумме квадратов:

 

                  ,                                           (3.6)

 

поэтому уравнение (3.4) имеет действительные решения.

         Если обозначить значение дискриминанта:

 

         ,                                                                                          (3.7)

 

то получим:

 

                                                                     (3.8)

 

а отсюда следует, что

 

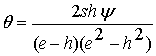                   .                                                       (3.9)

 

Назовем величину   углом нелинейности логики  , при этом получаем выражение отрицания высказывания через угол нелинейности:

 

                                                (3.10)

 

Теперь обозначим корни уравнения  (3.5)

 

                  

Затем найдём корни уравнения (3.4):

 

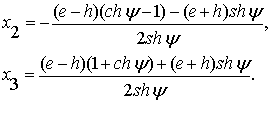                                                 (3.11)

         3.2.Отметим, что в силу положительности гиперболического косинуса получаем

 

                            .                                                (3.12)

 

Таким образом, можно сделать вывод о выполнении аксиомы (10) для квадратичного задания отделяющих функций: уравнение (3.3) можно записать в виде

 

         .                                         (3.13)

Поэтому условие

                                     

выполняется на интервалах

 

                                                                       (3.13)

а в остальных случаях выполняется неравенство противоположного смысла, что и означает, по мнению А.Г.Драгалина (см.[3]), интуиционистский характер системы аксиом (в соответствии с исчислением предикатов Гейтинга). Заметим, что первая часть в этом объединении не входит в область универсума. Поэтому окончательно можно сказать, что реальный интервал выполнения требований интуиционизма:

 

                                                                                         (3.14)

                   §  4.Симметричная модель логики

 

 

Для этой модели определяются отделяющие функции специального вида:

 

                                                                        (4.1)

При этом высказывание может быть записано в функциональном виде:

 

                                                             (4.2)

                                                                                       (4.3)

 

Теперь определяем отрицание истинности:

 

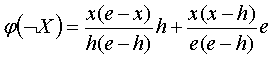                                                 (4.4)

 

Проводим небольшие вычисления, после чего получаем:

 

                                      (4.5)

 

Затем определяем двойное отрицание функции истинности:

 

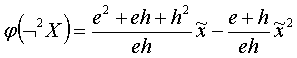                                                      (4.6)

 

После подстановки (4.5) в (4.6),  получаем следующую формулу:

 

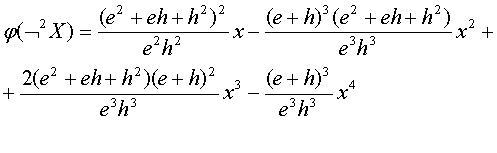            (4.7)

Для упрощения записи обозначим:

 

                  

 

Теперь находим разность между двойным отрицанием истинности и первоначальным значением  истинности:

 

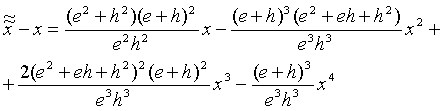                       (4.8)

 

  Чтобы проверить условие (4.9):

                                                                                               (4.9)

 

вводим новую функцию

 

здесь вычисления дают результат:

 

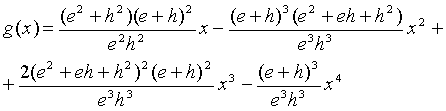                    (4.10)

 

Отсюда получаем:                                                                         

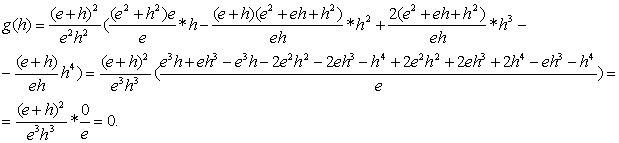
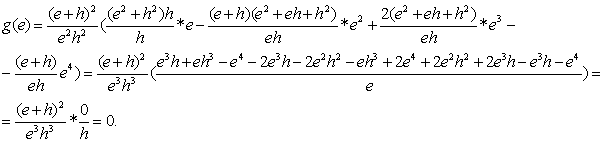
                                                                                                             (4.11)

 

Это означает, что кривая четвёртого порядка, определенная функцией g(x) пересекает ось (Ох) в точках {h,e}.

Так как данное уравнение имеет максимальную степень при x равную 4,   то уравнение имеет количество корней, равное 4. Мы нашли 3 корня из них. Найдем последний корень:

                                                     (4.12)

 

Теперь  находим значения   и  :

 

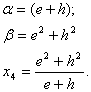                                                                                              (4.13)

 

После этих вычислений мы  определили все корни уравнения. Вследствие того, что выполняется условие (4.9),    выполняется и условие двойственного отрицания стандартной логики .

 

 

                                                                          

 

 

 

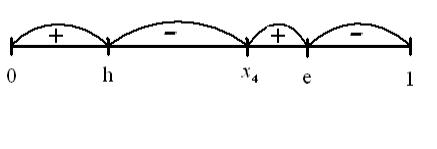
                                     Рис. 1

 

Теперь рассмотрим как себя ведет функция  на необходимых для анализа участках.

 Рабочий  интервал логической модели располагается от h до e. Следовательно из рис.1 у нас получается два случая:

 

         а)                                                                             (4.14)

         б) ,

 

значит, можно сделать вывод,   что  в случае (б)  условия двойного отрицания не выполняются, а в остальных случаях выполняются. Значит, нами найдена область выполнения условий логического интуиционизма для  построенной в случае симметрии    модели логической системы. Заметим, что этот результат (если учесть изменение обозначений) согласуется с полученной ранее формулой (3.14).

         Таким образом, мы изучили одну из проблем двузначной «мягкой» логической системы, связанную с выполнением условия двойного отрицания.

Отсюда можно сделать вывод, что четвертый блок, который в традиционном Аристотелевом универсуме отвергается, в случае «мягкой» модели может быть применен, что приводит к полному двойному покрытию этого универсума.

Этот материал заслуживает отдельного исследования.

 

 

 

                   ЛИТЕРАТУРА:

 

1. Гейтинг А. Интуиционизм. М. «Наука». 1965.

2. Клини С. Введение в метаматематику. М. «Наука».1957.

3. Драгалин А.Г. Математический интуиционизм. М. «Наука». 1979.

4. Евсеев В.И. Логическое обоснование семантических структур. //

  «Феномены природы и экология человека», т.3.  –  Сборник научных трудов и материалов пятого Международного Конгресса (26 – 28 мая 2008 г.) Казань. «Хэтер». 2008 (стр. 94 – 101).

5. Акбашев Р.А., Евсеев В.И. Моделирование аналитической семантики// Труды II Всероссийской научной конференции  «Информационные технологии в системе  социально-экономической безопасности России и ее регионов». Казань.2009 г.(146 – 154).