Математика/5. Математическое моделирование

                                   к.ф.-м.н. доц.  В.И. Евсеев  

Казанский  (Приволжский) федеральный университет, Казань, Россия  кафедра прикладной информатики

   УДК 681.32                        1 - vladislaw.evseev@yandex.ru, т.89047610772

 

О ПРИМЕНЕНИИ ФУНКЦИОНАЛЬНЫХ МЕТОДОВ

 

§ 1. Изучение стандартной конъюнкции в логике .

1.Для изучения конъюнкции введем два  суждения

                                                                              (1.1)                                                            

                                                                               

а также их структурные  симметрии

                                                                                (1.2)

          Стандартная конъюнкция определяется исходно простой формулой:  

                                                                                (1.3)

Матричное задание этой бинарной операции имеет вид:

 

    

 

    

 

                   

 

На основе этой  матрицы можем построить выражение для ее операции:

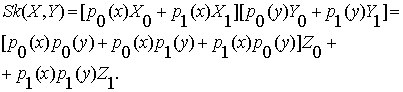                               (1.4)  

Значит, для конъюнкции получаем функцию истинности в логике

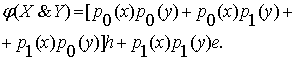                                               (1.5)

Поэтому матрица истинности конъюнкции такова:

    

 

 

 

 

           

                  

         Такая таблица может быть построена для каждой бинарной операции, а с ее помощью находится явное выражение функции истинности для любой из этих операций.

2.Теперь из формулы  (2.2.5) получаем явное выражение функции истинности:

                                                              (1.6)

Позволим себе не приводить все соответствующие вычисления.

Покажем на этом примере,  как в реальности работают функции истинности. Для этого вычислим по формуле (1.6) значения этой функции на конкретных классах истинности исходных аргументов:

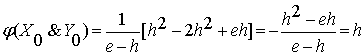,                                           (1.7)

,                                        (1.8)

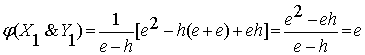.                                         (1.9)

         Эти результаты однозначно соответствуют матрице истинности .

 Поэтому получаем формулу для функции  классов этой конъюнкции:

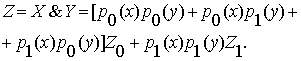                                                   (1.10)

 Аналогичные формулы получаются и для других бинарных операций. Мы сразу выделим операции типа «трап», а также общую истину и ложь, и не будем для них строить бинарные схемы, так как для операций типа «трап» они просто совпадают с соответствующими  унарными выражениями, а для двух последних не представляют интереса. Поэтому в дальнейшем будем рассматривать десять типичных бинарных операций, сохраняя их нумерацию в таблице, а также группы по уровням, что будет удобно ввиду большого информационного объема изложения.

Теперь перейдем к описанию функциональных представлений выделенных десяти бинарных операций.

§2. Функции истинности взаимных поляроидов

Два взаимных поляроида: левый поляроид              

                                                                                  (2.1)

и правый поляроид

                                                                                  (2.2)

отличаются только порядком применения структурной симметрии, поэтому их формулы имеют соответственную аналогию.  Так для левого поляроида найдем его реализующую матрицу:

     

 

    

                           

                  

 

из которой получим формулу

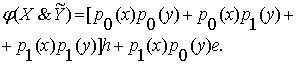                                              (2.3)                                 

         После соответствующих вычислений получаем результат:

                                                                    (2.4)

         По аналогии для правого поляроида сразу запишем результирующую формулу функции истинности:

                                                                  (2.5)

Проведем проверку результатов для левого поляроида:

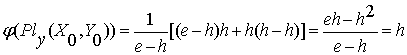,                                       (2.6)

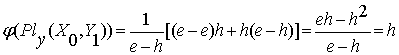,                                        (2.7)

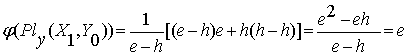,                                      (2.8)

 

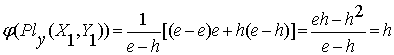.                                            (2.9)

         § 3 . Функции истинности нильюнкции и дизъюнкции

         Нильюнкция и дизъюнкция представляют собой две соинверсных бинарных операции, причем первая из них является конъюнкцией двух отсимметрированных ранее суждений:

,                                                                  (3.1)                               

а вторая операция представляет  ее внешнюю структурную симметрию:     

.                                                         (3.2)

Учитывая формулу (1.1.11), получим:

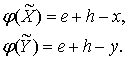                                                                                                  (3.3)

Отсюда непосредственно следует:

                               (3.4)

         После небольших преобразований получим окончательный результат:

 

                                                  (3.5)

         Мы не будем проводить проверку этих результатов, так как они сложностей не представляют.

         Теперь для дизъюнкции, как внешней структурной симметрии нильюнкции, получаем:

         .                    (3.6) 

Проверка здесь также проста, и мы не будем ее проводить. 

§4. Функции истинности взаимных импликаций

Дизъюнкция является бинарной операцией второго уровня, как и уже известная штокъюнкция.

Теперь перейдем к изучению взаимных импликаций.

Левая импликация имеет представление:

 

                                                              (4.1)

Значит, для ее функции истинности имеем:

 ,                     (4.2)

Что после небольших преобразований дает результат:

.                                (4.3)

Проверку проведем только для случая негативного результата:

.                        (4.4)

Для правой импликации по аналогии получаем:

 

                                                              (4.5)

Значит, формула для ее функции истинности такова:

 .                              (4.6)

Проверка здесь примитивна.

§  5. Функции истинности эквиваленции, хартъюнкции и штокъюнкции

 

Эквиваленция – это операция третьего уровня, как и ее структурная симметрия, называемая нами хартъюнкцией (старое название «строгая дизъюнкция»). Для эквиваленции получаем определяющую матрицу классов:

     

 

    

                           

                     = 

 

Отметим, что эквиваленция является конъюнкцией двух взаимных импликаций:

 .                                                         (5.1)

    Согласно таблице значений, получим общую формулу эквиваленции:

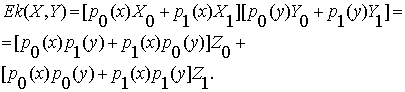                                     (5.2)

Применив функцию истинности, находим:

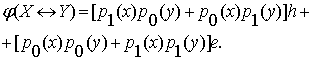                                                (5.3)

Проведя соответствующие преобразования, находим формулу для этой операции:

.                                                  (5.4)

Учитывая, что хартъюнкция – это взаимная операция к изученной уже эквиваленции, получим:

                    .                                                    (5.5)

Формула для ее функции истинности получается почти сразу же:

                                          (5.6)

Примечание: при построении этих формул можно применить свойства дизъюнкции

         а) дизъюнктивное сложение:

,                                                                              (5.7)                                 

б) взаимосвязь между   дизъюнкцией и хартъюнкцией                                                                         

                                                                       (5.8)

         Штокъюнкция, как операция, взаимная с конъюнкцией, имеет следующую функцию истинности:

          .                                       (5.9)

Мы не будем проводить проверку и в этом случае, так как она делается очень просто.

         Таким образом,    мы рассмотрели все основные бинарные операции и нашли для них функции истинности, которые   будут применены   при построении логико-семантической модели стандартной комплементарной структуры.

 

 

 

Литература:

1. Евсеев В.И. Логическое обоснование семантических структур. //

  «Феномены природы и экология человека», т.3.  –  Сборник научных трудов и материалов пятого Международного Конгресса (26 – 28 мая 2008 г.) Казань. «Хэтер». 2008 (стр. 94 – 101).

2. Акбашев Р.А., Евсеев В.И. Моделирование аналитической семантики// Труды II Всероссийской научной конференции  «Информационные технологии в системе  социально-экономической безопасности России и ее регионов». Казань.2009 г.(146 – 154).

3. Евсеев В.И. Семантический анализ комплементарной системы//Труды V международной научной конференции «Развитие и динамика иерархических (многоуровневых) систем». Казань. 20013.(221 – 226).