Математика/5. Математическое моделирование

к.ф.-м.н. доц. В.И. Евсеев

Казанский (Приволжский) федеральный университет, Казань, Россия, кафедра прикладной информатики

УДК 681.32 1 - vladislaw.evseev@yandex.ru, т.89047610772

О моделировании зонального семантического распределения

Аннотация:

Данная работа посвящена моделированию специфических зон, которые возникают в процессе изучения бинарных семантических групп, Построена авторская классификация этих зон и виды распределения групп по этим зонам.

Всюду указаны характеристические уравнения, отделяющие функции и определители построенных зон.

This work is aimed to the modeling of the specific areas that arise in the process of studying binary semantic groups, Built an author's classification of these zones and the types of distribution groups in these areas. Everywhere are the characteristic equation, separating the functions of the determinants of built areas.

Ключевые слова:

зоны сжатия, характеристическое уравнение, отделяющие функции семантических классов, определители групп бинарных операций.

1.1. Основные параметры бинарных операций.

Классификация, проведенная автором в [1], указывает на то, что все бинарные операции с семантической точки зрения подразделяются, прежде всего, на вырожденные и невырожденные. Вырожденные операции еще ждут своего изучения, а о невырожденных уже довольно много сведений дано в нашей монографии [2]. Из приведенной в первой цитированной работе таблицы следует, что часть из этих операций характеризуется различными значениями числа входящих конгруэнций (множеств однотипных аналитических суждений), а у остальных пара или тройка или две пары, или даже все эти значения могут совпадать.

Кроме того, даже условная информационная насыщенность у этих операций различна. Так, в указанной выше монографии на стр. 21 вводится понятие условной информационной загруженности суждений, которое затем, на стр. 50, связывается со значениями числа входящих в суждение конгруэнций.

Чтобы соединить эти два подхода проведем спецификацию этих значений. Будем, как и указано на стр. 21, считать, что - это параметры информационной насыщенности, удовлетворяющие условию:

, (1.1)

а само значение определяется как произведение нумерационных параметров выделенной группы суждений:

, , , ,

которые удовлетворяют соответственно условию:

. (1.2)

Поэтому получаем по данному предположению:

=, (1.3)

а также:

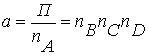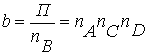, , (1.4)

, .

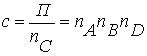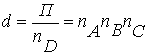В той же монографии на стр. 21 указываются и характеристическое уравнение данной группы, и ее отделяющие функции. Мы адаптируем эти формулы для случая заданных значений вхождения конгруэнций в рассматриваемую группу.

Таким образом, мы получаем уравнение данной семантики:

. (1.5) Отсюда получаются выражения для отделяющих функций конгруэнций, выраженных через нумерационные значения:

,

,

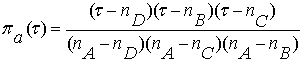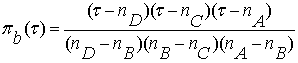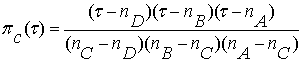, (1.6)

.

Теперь можно записать общее выражение суждения с помощью отделяющих функций и представителей четырех видов конгруэнций:

. (1.7)

Здесь существенную роль начинает играть определитель, определяющий различие входящих в эти формулы нумерационных параметров:

. (1.8)

Этот определитель не равен нулю только в том случае, когда все нумерационные значения различны. Если же среди этих значений есть одинаковые, то определитель становится равным нулю, а формулы (1.6) требуют изменения, так как в них будут входить степени линейных выражений. Значит, в классификации групп появляется новый критерий: различие или частичное совпадение нумерационных элементов, на чем мы и будем строить «зональную» классификацию семантических групп. Когда значения некоторых нумерационных элементов совпадают, мы будем вынуждены уменьшать размерность семантической группы и выделять соответствующий не равный нулю определитель.

Вторым критерием есть будет выступать реальное значение параметра информационной загруженности. В новой классификации для сохранения преемственности будем указывать также сами значения этих параметров и исходный номер группы по уже данной старой классификации.

1.2. Зональная таблица семантической классификации

Таким образом, мы приходим к следующим видам семантических зон, которые удобно будет начинать с нулевой зоны, в которой все нумерационные значения в группах различны.

Зона сжатия «0»:

≠ ≠ ≠, ≠0.

Здесь все отделяющие функции являются активно действующими и различными . Как будет далее показано, в эту зону входят девять групп (из 32).

Укажем сразу таблицу классификации этой нулевой зоны.

ТАБЛИЦА № 1.

Зональная классификация (зона 0).

ТАБЛИЦА № 1.

№ гр.
9	10	3	2	1	60	6	20	30	60
10	9	4	3	1	72	8	18	24	72
11	8	5	2	1	80	10	16	40	80
12	7	6	2	1	84	12	14	42	84
14	8	4	3	1	96	12	24	32	96
15	7	5	3	1	105	15	21	35	105
18	6	5	4	1	120	20	24	30	120
26	7	4	3	2	168	24	42	56	84
27	6	5	3	2	180	30	36	60	90

Когда пара значений совпадает, возможны следующие случаи:

Зона сжатия 1.1. (=).

По этому условию совпадают только выделенные значения количества представителей первой пары конгруэнций. Сюда входит девять семантических групп бинарных операций.

ТАБЛИЦА № 2.

№ гр.
2	12	2	1	1	24	2	12	24	24
3	11	3	1	1	33	3	11	33	33
4	10	4	1	1	40	4	10	40	40
9	9	5	1	1	45	5	9	45	45
6	8	6	1	1	48	6	8	48	48
21	9	3	2	2	108	12	36	54	54
22	8	4	2	2	128	16	32	64	64
23	7	5	2	2	140	20	28	70	70
31	6	4	3	3	216	36	54	72	72

Зональная классификация (зона 1.1.)

Зона сжатия 1.2. (=)

Здесь количественно совпадают только вторая и третья по виду конгруэнции. При этом присутствует шесть групп бинарных операций.

Таблица № 3

Зональная классификация (зона 1.2.).

№ гр.
8	11	2	2	1	44	4	22	22	44
13	9	3	3	1	81	9	27	27	81
17	7	4	4	1	112	16	28	28	112
25	8	3	3	2	144	18	48	48	144
28	6	4	4	2	192	32	48	48	96
33	5	4	4	3	240	48	60	60	80

Зона сжатия 1.3. (=)

В этой зоне одинаковые значения имеют третий и четвертый вид конгруэнций.

Этим свойством обладает две семантические группы бинарных операций.

Таблица № 4

Зональная классификация (зона 1.3.).

№ гр.
16	6	6	3	1	108	18	18	36	108
29	5	5	4	2	200	40	40	50	100

Зона сжатия 2.2

В эту зону входят семантические группы, у которых две пары конгруэнций одинаковы по значениям: одновременно

=, =.

Таких всего три группы.

Таблица № 4

Зональная классификация (зона 1.3.).

№ гр.
7	7	7	1	1	49	7	7	49	49
24	6	6	2	2	144	24	24	72	72
32	5	5	3	3	225	45	45	75	75

Зона сжатия 3.1

В эту зону входят те группы, у которых ==,

Такого типа также имеется три группы:

Таблица № 5

Зональная классификация (зона 3.1.).

№ гр.
1	13	1	1	1	13	1	13	13	13
20	10	2	2	2	60	6	30	30	30
30	7	3	3	3	189	27	63	63	63

Зона сжатия 3.2

Осталось рассмотреть один случай совпадения значений

==, для которого получаем:

Таблица № 6

Зональная классификация (зона 3.2).

№ гр.
19	5	5	5	1	125	25	25	25	125

Зона сжатия 4.1

Кроме того, для предельной группы №34 также нужно построить таблицу классификации, учитывая, что здесь:

====4.

Таблица № 7

Зональная классификация (зона 4.1).

№ гр.
34	4	4	4	4	256	64	64	64	64

1.3. Уравнения и функции зон бинарных операций.

Укажем в каждой зоне (для нулевой зоны это уже сделано) вид характеристического уравнения и отделяющих функций, а также вида соответствующего определителя зоны с учетом проведенной классификации. Мы начинаем, таким образом, с первой зоны сжатия.

Зона сжатия 1.1. (=).

Здесь характеристическое уравнение принимает вид:

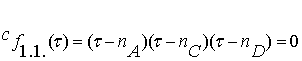(3.1)

Значит, отделяющие функции при этом таковы:

,

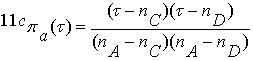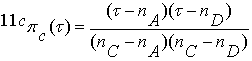, (3.2)

.

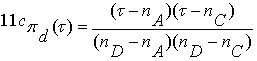Определитель этой семантической группы принимает вид: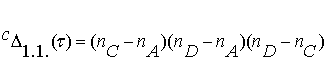. (3.3)

Зона сжатия 1.2. (=).

Для этой зоны получаем характеристическое уравнение: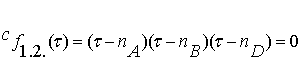 (3.4)

Следовательно, здесь отделяющие функции таковы:

,

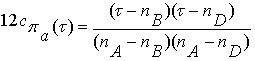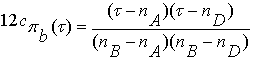, (3.5)

.

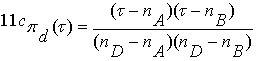Следовательно, находится и сам определитель этого типа групп: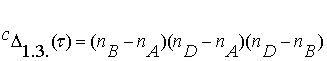. (3.6)

Зона сжатия 1.3. (=)

В этом случае характеристическое уравнение принимает вид: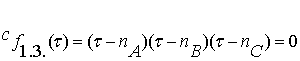 (3.7)

Также получаем по известной уже методике отделяющие функции конгруэнций в этих группах:

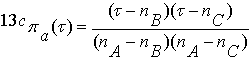
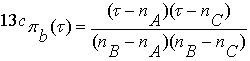, (3.8)

.

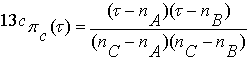Определитель этого вида групп получается следующим:

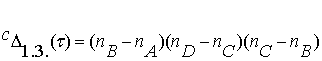. (3.9)

Зона сжатия 2.2. (=, =).

В этой зоне характеристическое уравнение становится квадратным:,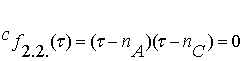

поэтому отделяющие функции становятся линейными:

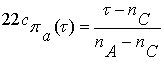, (3.10)

.

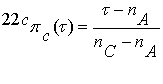Соответственно, определитель этого вида групп:

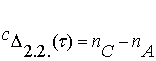. (3.11)

Зона сжатия 3.1.

Здесь получаем условия: ==,

Поэтому характеристическое уравнение также является квадратным:

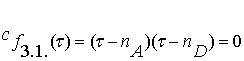, (3.12)

а отделяющие функции – линейные:

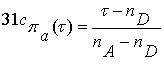, (3.13)

.

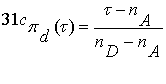При этом здесь находится определитель:

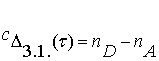. (3.14)

Зона сжатия 3.2. (==).

Здесь мы сразу же получаем квадратное характеристическое уравнение: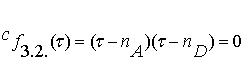, (3.15)

отделяющие функции классов:

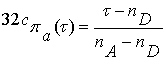, (3.16)

.

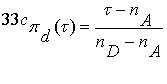Определитель этой системы групп следующий:

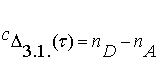. (3.17)

Зона сжатия 4.1. (====4).

У предельной группы характеристическое уравнение оказывается линейным:

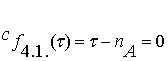, (3.18)

А отделяющая функция – простейшей:

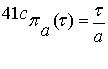. (3.19)

Определитель этого вида групп:

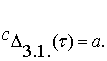(3.20)

Таким образом, мы изучили семантические зоны сжатия для всех невырожденных групп бинарных операций.

Литература:

1. Евсеев В.И. О методике моделирования логических систем// Материалы международной научно-практической конференции»ИТОН 2012, Казань (222 – 231).

2. Евсеев В.И. Основы аналитической семантики. Изд. «Lambert». 2014 г.

(165 стр.).

3. Евсеев В.И. О системе семантических бинарных операций//Ученые записки Казанского института гуманитарных и социальных знаний,

№ 2(10), Казань, 2012 г.(29 – 39).