Математика/математическое
моделирование
УДК 593.3
К.ф.-м.н.
Т.И. Некипелова
Бурятский
государственный университет, inltavo@mail.ru
К.ф.-м.н.,
д.п.н. В.Б. Цыренова
Бурятский
государственный университет, v.ts@mail.ru
КОНТАКТНОЕ ВОЗДЕЙСТВИЕ
ЖЕСТКОГО ЭЛЕМЕНТА НА УПРУГОЕ ПОЛОЕ ЦИЛИНДРИЧЕСКОЕ ТЕЛО
В работе вычисляются максимальные
локальные напряжения, возникающие в зоне контакта цилиндра с жестким элементом.
Начальное решение производится в перемещениях. Для решения задачи используется
равномерная сетка по каждому из трех координатных направлений.
Ключевые слова: контактное воздействие, упругие перемещения точек,
обобщенный закон Гука, касательные и нормальные напряжения, метод простой
итерации, центральная аппроксимация.
Рассмотрим уравнения равновесия в перемещениях в цилиндрической системе координат:
(1)
, (2)
(3)
где
- окружное,
радиальное и осевое смещения; 
- цилиндрические координаты; 
- плотность
среды; 
- проекции массовой силы на оси выбранной системы
координат; 
- модуль упругости при сдвиге; 
- коэффициент Пуассона; 
- модуль Юнга; 
- оператор Лапласа; 
- объемная деформация. Рассмотрим случай 
. В уравнениях (1)-(3) подставим 
, раскроем оператор 
. Умножив каждое из уравнений (1)-(3) на 
и применив центральную аппроксимацию, получим следующие уравнения в перемещениях: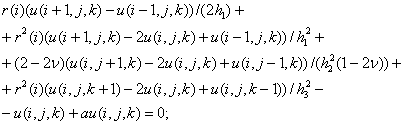 
(4)
(5)
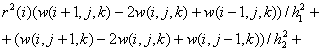
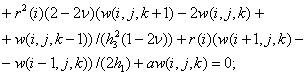(6)
где
- шаги сетки соответственно по 
,
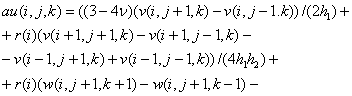
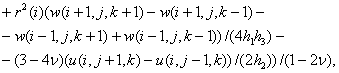
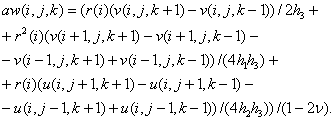
Из
соотношений (4)-(6) найдем 
Введем
следующие обозначения:
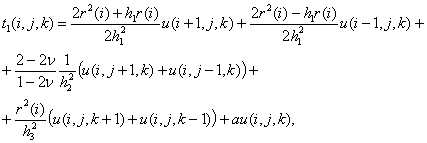
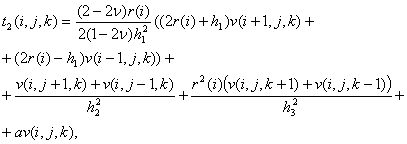
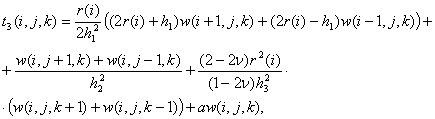
Запишем
формулы для определения значений перемещений во внутренних точках: 
(7)
Рассмотрим
полый цилиндр следующих размеров: 
- внешний радиус цилиндра, 
- внутренний радиус цилиндра, 
- высота
цилиндра, 
-коэффициент
Пуассона, 
Внешнее
воздействие на цилиндр зададим осевым смещением 
. Найдем максимальные напряжения, возникающие в зоне
контакта. Зададим начальные граничные условия. Для точек верхнего основания 
Для других
граничных точек цилиндра 
Пусть
, где 
- число делений
соответственно по радиусу, окружности и оси цилиндра. Приведем формулы,
позволяющие производить итерационный перерасчет значений 
для поверхностных
точек цилиндра. Для точек верхнего основания
Для
точек внутренней боковой поверхности
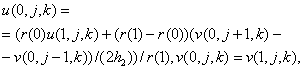
Для точек внешней боковой поверхности:
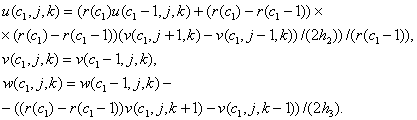
Для точек нижнего основания:
Для
внутренних точек цилиндра итерационный перерасчет производится по формулам (7).Условие
периодичности выражено следующими соотношениями: 
Получив
числовые массивы окружного, радиального и осевого смещений
, найдены числовые массивы напряжений из обобщенного
закона Гука 
Максимальные
напряжения в зоне контакта: max(
)=124; max(
)=263; max(
)=112. На рис.1- рис.3 представлены напряжения соответственно
и их осевые сечения в зоне контакта.
Рис.1
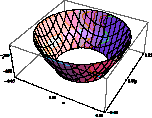
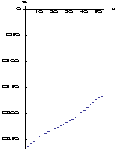
Рис.2
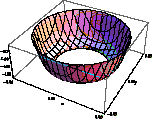
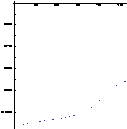
Рис.3
ЛИТЕРАТУРА
1.
Демидов С.П. Теория упругости. – М.: Высшая школа, 1979. – 340 с.
2.
Бубенчиков А.М., Бубенчиков М.А., Некипелова Т.И., Цыренова В.Б., Щербаков Н.Р.
Контактное воздействие жесткого элемента на упругое тело цилиндрической
формы.// Вестн. Томск. гос. ун-та. Матем. и мех. 2012, номер 3, стр. 41-48.
Tatjana I.
Nekipelova
Institute
of Mathematics and Informatics, Buryat
State University,
Ulan-Ude, Russia,
inltavo@mail.ru
Valentina B.
Tsyrenova
Institute
of Mathematics and Informatics, Buryat
State University,
Ulan-Ude, Russia, v.ts@mail.ru
CONTACT
IMPACT OF HARD ON THE ELASTIC HOLLOW CYLINDRICAL BODY
We propose a computation technology that realizes the problem of the
lineal theory of elasticity in cylindrical coordinates. Particular attention is
paid to the area of contact between two bodies. To expand it a uniform grid for
each of the three coordinate directions is used.
Keywords: contact action, the elastic displacement of the
points, generalized Hooke’s law, the tangential and normal stresses, a simple
iteration.