А. И. Федотов д.т.н., С.К. Лисин к.т.н.

СПб государственный политехнический университет, СПб национальный минерально-сырьевой университет «Горный», Россия

НЕЛИНЕЙНЫЕ МЕТОДЫ МИНИМИЗАЦИИ ТЕОРИИ ИЗМЕРЕНИЙ

Направления исследований теории минимизации представляют широко используемую и эффективную систему методов определения и оптимизации параметров опытов. В процессе восстановления опытов возникает необходимость формализации представления процедур измерений с целью сокращения формы записи экспериментальной информации, например в задаче сопоставления функции шкалы прибора с полученными результатами измерений.

Такие процедуры связаны с рассмотрением моделей невязок, обусловленных отклонениями экспериментальных данных. Для описания _{свойств ряда технических объектов, с помощью их приближенных моделей используется линейный вариант метода наименьших квадратов, позволяющий минимизировать сумму квадратов отклонений искомых параметров. В рамках конкретных метрологических задач экспериментальные зависимости строятся с целью установления связи между независимыми переменными и неизвестными параметрами функций воспроизведения отклонений опытов [1,2] и др.}

В теории измерений повторяемых опытов возникает необходимость построения системы уравнений, содержащей сравнительно небольшое число неизвестных величин по сравнению с числом уравнений соответствующих процедур измерений. Для применения метода наименьших квадратов исходная система результатов опытов приводится к нормальной системе, число уравнений которой равно числу неизвестных исходной системы [1,3]. В этом случае система уравнений относительно неизвестных исследуемого объекта, процесса или опыта имеет вид

y₁ = а₁₁х₁ + а₁₂х₂ + … + а_1n х_n ,

y₂ = а₂₁х₁ + а₂₂х₂ + … + а_2nх_n , (1)

………………………………...

y_m = а_m1х₁ + а_m2х₂ + … + а_mnх_n .

Матричные преобразования (1) становятся необходимыми при оценке свойств измеряемых объектов [4,5]. _{При этом общей задачей регрессионного анализа является определение связи между неизвестными величинами и контролируемыми переменными, определяемыми по результатам прямых измерений.}

В практике измерений и контроля чаще всего неизвестные величины входят или в трансцендентные выражения, или имеют степени высших порядков. При этом можно выделить два варианта применения нелинейного метода наименьших квадратов: нелинейная аппроксимация (преобразование исследуемой функции в более простую функцию) и оценивание нелинейных параметров. Естественно предположить, что второй вариант чаще всего используется в прикладных задачах теории измерений.

Следовательно, проблема восстановления нелинейных функций является актуальной и важной. Рассмотрим, например, типовую задачу восстановления функциональной зависимости, теоретическая модель которой имеет вид

y = f(x; u).

Исследуемая функция f(x; u) является нелинейной зависимостью от значений u_i вектора u = (u₁ … u_m)_t, которые подлежат определению. Будем полагать, что при заданных контролируемых переменных x = x_i , i = 1 … n производится отдельное измерение у_i, обусловленное его случайной погрешностью s_i

y_i = f(x_i ; u) +s_i .

В общем виде система нелинейных уравнений отдельных измерений будет иметь вид

A(u) = Y - s. (2)

В процессе определения и анализа параметров (2) становятся актуальными задачи восстановления функций или систем уравнений, устанавливающих связь между контролируемыми переменными и результатами измерений. При этом естественно полагать, что достижению поставленной цели, то есть построению системы уравнений только на основе результатов опытов, адекватно отражающих свойства исследуемых объектов, будет предшествовать анализ априорной информации и соответствующих локальных моделей. С другой стороны может оказаться важнейшим рассмотрение двух направлений:

- установление источников наиболее вероятных нерегламентированных в нормативно-технической документации погрешностей;

- выявление механизма отказов, нарушений функционирования приборов или появления непредсказуемых результатов измерений.

В конечном итоге подобная совокупность соблюдения условий, статистических ограничений, требований к качеству продукции приводит к необходимости поиска путей повышения точности и качества продукции.

Рассмотрим в качестве примера характерную для теории измерений задачу определения оценок неизвестных параметров и восстановления нелинейной функции экспериментальной системы. Подобная теоретическая модель плотности распределения вероятности отдельных измерений имеет вид

.

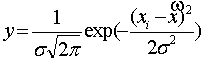В этом случае система уравнений относительно неизвестных σ и исследуемого опыта записывается в виде:

,

,

. . .

.

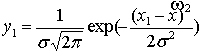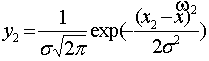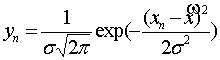Теоретическая модель восстанавливаемой функции имеет вид

y = f(x; z).

В рассматриваемом случае f(x; z) является нелинейной зависимостью от значений z_i вектора z = (z₁ … z_m)_t, которые подлежат определению. Будем полагать, что с учетом контролируемых переменных x = x_i , i = 1 … n производится отдельное измерение у_i, обусловленное его случайной погрешностью δ_i

y_i = f(x_i ; z) +δ_i.

В матричном представлении система нелинейных уравнений данной задачи имеет вид

A(z) = Y - δ. (9)

Элементы матрицы векторного пространства можно представить зависимостями A(z) = (f(x₁, z) … f(x_n, z)); Y = (y₁ … y_m); δ = (δ₁ … δ_m).

Предположим, что погрешность δ_i не имеет статистической связи. Определим оценку искомого вектора z (9) с помощью типового равенства

z = arg min ||A(z) – Y ||² . (10)

Оценка z характеризуется невязкой вида (10) и может быть представлена функционалом L(z)

L(z) = (A_i (z) – y_i)².

Здесь A_i(z) является одной из компонент вектор - функции A(z).

Предположим, что по условию опыта мы имеем n уравнений, связывающих результат измерения y_i контролируемую переменную x_i и неизвестные параметры модели z₁, z₂, …, z_m

Y_i = f (z₁, z₂, … , z_m; x_i), i = 1,…, n .

Неизвестные параметры z₁, z₂, …, z_m находятся из условия минимума квадратичного функционала L

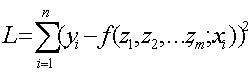. (11)

В качестве начальных приближений оцениваемых параметров выберем значения и разложим нелинейную функцию f(z₁, z₂, …, z_m; x_i) в ряд Тейлора в окрестности выбранной точки z⁰, ограничив разложение линейными членами. При этом исходный функционал L будет представлен функционалом L₁

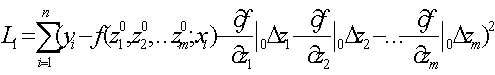. (12)

Разрешив нормальную систему уравнений подобную (7) методом обратной матрицы, определим приращения параметров Δz₁, Δz₂, … , Δz_m. Процесс нахождения решений системы определяется выбором начальных приближений параметров по аналогичному алгоритму

z_i^k+1 = z_i^k + Δz_i^k .

Итерационный процесс нахождения решений будет сходящимся, если функционалы L и L₁ эквивалентны относительно их общего минимума, а разложение функции f(z₁,z₂, …, z_m; x_i) в ряд Тейлора будет выполнено в линейном приближении.

Реализация предложенных математических моделей позволяет с одной стороны минимизировать отклонения восстанавливаемых по результатам наблюдений функций исследуемых объектов, а с другой стороны определить погрешности искомых параметров и системы с помощью эквивалентных функционалов оценок.

Л и т е р а т у р а:

1. Линник Ю. В. Метод наименьших квадратов и основы математико–статистической теории обработки наблюдений. Л. Физматгиз, 1962. – 352 с. 2. Феллер В. Введение в теорию вероятностей и ее приложения (т.2).- М.: Изд-во «Мир», 1967. – 752 с.

3. Шишкин, И.Ф. Теоретическая метрология. Ч.1. Общая теория измерений: учеб-метод. комплекс: (учеб. пособие), /И.Ф. Шишкин (3-е изд., перераб. и доп.). – СПб.: Изд–во СЗТУ, 2008. – 189 с.

4. Лисин С.К., Федотов А.И. Научно – технические ведомости № 3 –СПбГПУ, 2009, с. 181-184.

5. Лисин С.К. Теория и средства измерений / С.К. Лисин, А.И. Федотов. – СПб. : Изд-во Политехн. ун-та. 2010. – 260 с.

6. Федотов, А.И. Теория измерений / А.И. Федотов, С.К. Лисин, Г.С. Морокина. – СПб.: Изд-во Политех. ун-та, 2013. – 325 с.

_{Авторы: А.И. Федотов}

_{С.К. Лисин}