3

К. ф.-м. н. Д.И. Масленников.

Харьковский национальный аграрный университет им. В.В. Докучаева, Украина

Распад мощной неоднородной волны накачки в плазме с ионами одного сорта на две нижнегибридные волны.

Аннотация. Рассмотрен распад нижнегибридной волны накачки на две нижнегибрижные волныв плазме с ионами одного сорта в случае, когда осцилляторные скорости частиц плазмы в поле волны накачки сравнимы с тепловыми скоростями. На основе метода, предложенным автором ранее, определены механизмы возбуждения неустойчивости в зависимости от длины волны возникающих колебаний. Сделана оценка инкремента неустойчивости. Установлен возможный уровень насыщения неустойчивости вследствие нелинейного сдвига частоты.

Ключевые слова: плазма, распадная неустойчивость, нижнегибридные волны, инкремент, нелинейный сдвиг частоты, насыщение неустойчивости.

Постановка проблемы в общем виде. Воздействие на плазму мощной электромагнитной волны (поля накачки) является одной из центральной задач в физике плазмы. Практическое значение в исследовании этих явлений определяется их связью с проблемой нагрева и создания плазмы электромагнитными волнами, с рядом задач плазменной электроники (например, коллективное ускорение частиц плазмы), с исследованием волновых явлений в ионосфере. В многочисленных экспериментах по нагреву плазмы электромагнитными волнами (см., например, [1-3]) были зафиксированы параметрические неустойчивости плазмы. Теория параметрических неустойчивостей была развита во многих работах, однако, ряд важных проблем все еще остается не решенными.

Анализ последних достижений и публикаций. Теория параметрических неустойчивостей в случае мощного поля накачки основывается на двух методах. В первом методе, который использует дипольное приближение (, где -волновой вектор волны накачки) [4], неустойчивости возбуждаются вследствие относительного колебательного движения компонентов плазмы в поле волны накачки. В этом приближении исследование распадных неустойчивостей ограничено распадом волны накачки на две волны, которые распространяются в противоположных направлениях и удовлетворяют условию . Второй метод (см. [5,6]) основывается на формализме слабых нелинейных взаимодействий волн. Волна накачки и волны, возбуждающиеся вследствие параметрической связи, являются величинами первого порядка малости по амплитуде колебаний, параметрическая связь обеспечивается учетом слагаемых второго порядка малости. Этот подход подразумевает слабую волну накачки, когда скорость осцилляторного движения частиц плазмы, которая пропорциональна амплитуде волны накачки, меньше тепловой скорости частиц плазмы.

Формулировка целей статьи. В работах [7,8] развит новый метод обобщающий оба вышеуказаных метода на случай мощных волн накачки с конечной длиной волны (). В настоящей работе на основе этого метода проводится исследование линейной и нелинейной стадий распада волны накачки на две нижнегибридные волны.

Изложение основного материала. Рассматривается плазма с ионами одного сорта, находящуюся в постоянном магнитном поле и переменном электрическом .

Условие распада имеет вид:

, где обозначено . (1)

Собственные частоты волн, участвующих в распаде определяются уравнением , (2)

где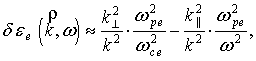

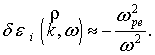
При уравнение (2) дает

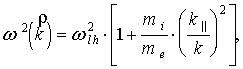где (3)

Индекс || означает составляющую, параллельную магнитному полю.

Условие резонансного распада приобретает вид

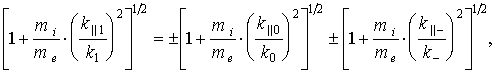
В работе [7] получена нелинейная система уравнений для амплитуд потенциала и волн распада мощной волны накачки с конечной длиной волны:

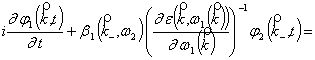
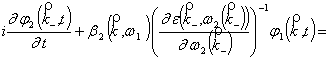
, (4)

где коэффициенты параметрической связи и состоят из двух слагаемых:

. (6)

Первое слагаемое описывает возбуждение распадной неустойчивости в результате относительного движения компонентов плазмы в поле волны накачки, второе – вследствие нелинейного отклика компонентов плазмы на волну накачки.

Величины и определяются известными выражениями (см., например, [7])

, где

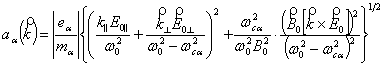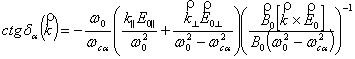Громоздкие выражения для величин и коэффициентов (=1,2,3,4), описывающих явление нелинейного сдвига частоты, приведены в работах [7,8].

Из системы (4) при =0 получается система уравнений, описывающая линейную стадию развития неустойчивости, из которой находится инкремент распадной неустойчивости [8].

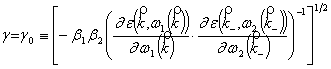(7)

Оценки величин, входящих в коэффициенты параметрической связи β, показывают, что

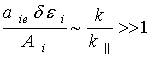То есть, вклад ионов в коэффициенты та в (6) несущественен. Если волновые вектора такие, что

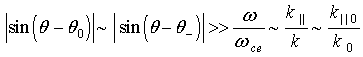, (8)

для электронных коэффициентов получаем соотношение:

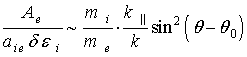. (9)

Из (9) следует, что возбуждение нижнегибридных волн в интервале углов , для которых выполняется неравенство

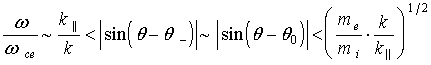, (10)

возникает преимущественно вследствие колебаний электронов относительно практически неподвижных ионов. В этом случае

(11)

и инкремент возбуждения неустойчивости оценивается как

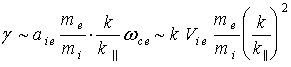. (12)

В интервале углов , где выполняются неравенство (8) и неравенство

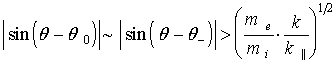, (13)

основным механизмом возбуждения донного распада является нелинейный отклик электронной компоненты плазмы на нижнегибридную волну накачки. В этом случае получаем для коэффициентов та

. (14)

И инкремент неустойчивости оценивается следующим образом:

. (15)

Если же волны і распространяются в направлениях, где

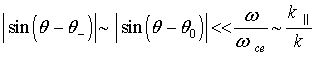, (16)

то получаем оценку коэффициентов параметрической связи β

И инкремент неустойчивости оценивается следующим образом:

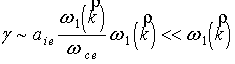. (17)

Рассмотрим возможность насыщения нижнегибридной распадной неустойчивости вследствие нелинейного сдвига частоты волн распада. Как показано в [7,8], состояние насыщения неустойчивости определяется условием

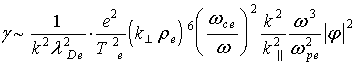, (18)

где - большая из і амплитуд волн распада. Из (18) получаем оценку для плотности энергии колебаний (где ) в состоянии насыщения:

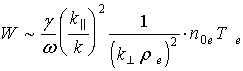. (19)

Заключение. Построена линейная теория распада волны накачки на две нижнегибридные волны в случае соизмеримых длин волн распада, . Показано, что наряду с нелинейным коллективным откликом плазмы на волну накачку, не менее важным источником возбуждения распада является осцилляторное движение электронов относительно ионов в поле накачки конечной длины волны .Получены выражения для коэффициентов параметрической связи и инкрементов в случае , определены области параметров, для которых преимущественным оказывается один из двух вышеуказанных механизмов возбуждения распадной неустойчивости.

Выяснена роль нелинейного сдвига частоты в насыщении данной распадной неустойчивости, сделана оценка плотности энергии неустойчивых колебаний в состоянии насыщения.

Литература.

1. Porkolab M. Nuclear fusion, 1978. Vol.18, P.367.

2. Ono M., Porkolab M., Chang R.P.H. Phys. rev. Lett., 1977, Vol.38, P. 962.

3. Ono M., Porkolab M., Chang R.P.H. Phys.Fluids, 1980, Vol.23, P.1656.

4. Kitsenko A.B., Stepanov K.N. Zh. Exper. Teor.Fiz. 1973, Vol.64, P.1606.

5. Ораевский В.Н., Сагдеев Р.З. Об устойчивости установившихся продольных колебаний плазмы. // ЖТФ. - 1962. - Т.32, № 1. - С. 1291-1296.

6. Liu C.S., Tripathi V.K. // Phys. Reports. 1986. V. 130. P. 143.

7. Масленников Д.И., Михайленко В.С., Степанов К.Н. Нелинейная теория ионной циклотронной параметрической распадной неустойчивости плазмы с ионами одного сорта // Физика плазмы. - 1995. - Т. 21, № 9. - С. 791-805.

8. Масленников Д.И., Михайленко В.С., Степанов К.Н. Ионные циклотронные распадные неустойчивости плазмы с ионами двух сортов в поле сильной неоднородной волны накачки // Физика плазмы. - 1997. - Т. 23, № 12. - С. 1088-1103.