Кошимбаев Ш.К. , Иманбекова У.Н.

Казахский национальный технический университет имени К.И.Сатпаева, г. Алматы, Республика Казахстан

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КОНВЕРТОРНОЙ ПЛАВКОЙ МЕДНЫХ КОНЦЕНТРАТОВ

В данной статье описывается оптимальное управление конверторной плавкой технологического процесса электроплавки медных концентратов. Такая модель позволит решать задачи технологического проектирования процесса, выбора наилучших конструктивных и режимных параметров электропечи. В работе проводится анализ основных статистических показателей оптимальных систем управления процессами шихтовки и плавления медных концентратов, при плавке обеспечивающих уменьшение потерь металла и энергозатрат. В данной статье на основании использования особенностей технологии процесса конвертирования и задачи управления получены эффективные в вычислительном плане алгоритмы управления конверторной плавкой, обеспечивающие достижение желаемого технологического эффекта при оптимальном управлении плавкой. Множество стехиометрических уравнений, описывают процесс конвертирования, а моделирование параллельно протекающих реакций системой алгебраических уравнений основано на учете приоритетности протекания реакций, которая выбрана на основе термодинамических закономерностей.

В последние годы развитие металлургии меди характеризуется повышением использования сырья, применения кислорода, автоматизированием управляемых процессов шихтовки и плавления медных концентратов. Это можно решить с помощью неопределенной математической постановки. Промышленные опыты показали, что температура плавящейся шихты в печи изменяется с некоторой инерцией. Шихта в печи плавится электродами под высоким напряжением и температура шихты с низкого показателя на более высокий не сразу переходит и соответственно наоборот.

Содержательная и математическая постановка задачи управления плавкой. Задача оптимального управления конверторной плавкой заключается в формировании оптимального графика плавки и оперативной корректировке его в ходе процесса. Необходимость корректировки графика определяется величиной отклонения достигнутого состояния процесса за очередную продувку от заданного состояния, , т. е. если отклонение ∆X после n-ой продувки больше допустимого ∆x , то производится корректировка (формирование) графика на оставшиеся продувок, где количество продувок в q-ой плавке [1].

Таким образом, основное содержание задачи управления плавкой составляет задача формирования оптимального графика плавки, заключающееся в определении количества продувок на q-ую плавку, распределении по продувкам количества штейна дутья руды и длительность продувок для всех обеспечивает переработку заданного план графиком работы конверторного отделения количества штейна на q-ую плавку минимальным отклонением от заданного времени плавки , а также с минимальным количеством меди в шлаке , отклонением содержания кремнезема в шлаке и температуры расплава от величины, установленных технологическими нормами.

Здесь и далее будем использовать следующие обозначения:

- соответственно количество i-го материала, j-го вещества в i-ом материале, загруженном или образовавшемся в конверторе в n-ую продувку (т. е. на интервале ;

- среднее значение величины расхода i -го материала в n-ой продувке;

- соответственно температура i -го материала и доля у -го вещества в i -ом материале,

загруженном в n-ую продувку или полученном в n-ой продувке;

{i} - множество индексов {i}= {1,2,..., 8}, которым обозначено: 1-штейн; 2 - дутье; 3 - руда; 4 - заливаемый конверторный шлак; 5 - холодные обороты; 6 - шлак в ванне конвертора; 7 - отходящий конверторный газ; 8- сульфидная масса в ванне конвертора;

{j} - множество индексов {j} = {1,2,..., 15}, которым обозначено: 1 - Си (общая); 2 - Fe; 3 - S; 4 -0₂; 5 - N₂; 6 -S0₂; I - Cu₂S, 8 - FeS; 9 - Cu₂0; 10 - FeO; 11- Fe₃0₄; 12 - Si0₂, 13 - (FeO)SiO₂ 14 - прочие вещества; 15 - Cu (металлическая);

- длительность n-ой продувки.

В приведенной формулировке графика конверторной плавки представляет собой задачу оптимального управления многостадийным периодическим процессом. Решение подобной задачи является весьма сложным [2].

Одним из возможных подходов к решению этой задачи является подход, основанный на анализе технологических особенностей объекта управления и позволяющий заменить решение исходной задачи решением нескольких, но существенно менее сложных задач.

Сформулируем ряд положений, основанных на изучении технологических особенностей существующей практики конвертирования медных штейнов и физико-химических закономерностей процесса.

По отработанной технологии ведения процесса конвертирования распределение штейна по продувкам осуществляется не более чем в одном двух вариантах. Возможные варианты распределения штейна по продувкам (в ковшах штейна на продувку) фиксируются, как правило; картой технологического режима. Для условий работы конверторного отделения медь завода ДГМК ЖМЗ характерной является следующая практика: в первую продувку (на зарядку) загружается два три ковша штейна, в каждую последующую загружается по одному ковшу, при этом последняя продувка первого периода (продувка на "белый матт") является "холостой", т.е. производится без загрузки штейна. Заключительная продувка плавки ("варка меди")также осуществляется без загрузки штейна. Таким образом, число продувок конверторной плавки и распределение штейна по продувкам для принятого числа ковшей штейна на первую продувку и определенного графиком конверторного отделения числа ковшей штейна являются известными величинами.

Анализ физико-химических закономерностей процесса позволяет разделить выделенные выше критерии оптимального управления плавкой на две группы: первой отнесем и , а ко второй и . Такое разделение основано на существенно различном влиянии искомых управлений [n], [n] и на эти показатели [3].

Для первой группы характерно незначительное влияние относительно небольших (вследствие стабилизации температуры на уровнях управления плавкой и процессом) колебаний температуры расплава на содержание меди и кремнезема в конверторном шлаке. Содержание меди в шлаке и, в конечном итоге, общее количество меди в шлаке за плавку зависит, главным образом, от глубины продувки (степени обогащения) сульфидной массы в ванне конвертора в каждой продувке, т. е. от количества дутья [n] и руды [n], подаваемых в каждой продувке. Эту особенность можно условно выразить следующей зависимостью:

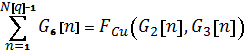, (1)

Если учесть, что количество загружаемой кремнистой руды в первую очередь определяется необходимостью получения определенного химического состава шлака, то можно принять количество руды на продувку [n] пропорциональным количеству дутья [n], т.е. пропорциональным количеству образующихся окислов железа, подлежащих ошлаковыванию, где с учетом стехиометрических соотношений реакций окисления и шлакообразования и содержания кислорода и кремнезема соответственно в дутье и руде можно представить в следующем виде:

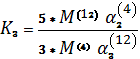* (2)

здесь коэффициент, определяющий долю избыточного (свободного кремнезема в конверторном шлаке).

Используя этот прием, можно считать, что содержание кремнезема в шлаке будет находится в необходимых по технологии процесса пределах, вследствие чего критерий удовлетворяется в достаточной мере (справедливость этого предложения подтвердилась экспериментальных исследований).

Анализ связи второй группы критериев с переменными состояния процесса показывает, что температура расплава в ванне конвертора зависит от количества поданных на продувку дутья, руды и длительности продувки, в общем, виде эту зависимость можно выразить соотношением:

(3)

С учетом приведенных особенностей видно, что исходная задача формирования оптимального графика конверторной плавки распадается на решение двух и белее простых задач: распределение количества дутья по продувкам и определения длительности продувок, при этом последовательность решения задач определяется характером зависимостей (3.1.1) и (3.1.2): для заданных условий (количество штейна на плавку, химсоставов штейна, дутья и руды) определяются оптимальные в смысле критерия величины , затем с учетом найденных величин и заданной длительности плавки τ[q] определяются значения оптимальные в смысле критерия, учитывающего показатели и .

Задача распределения дутья должна обеспечить переработку заданного на q-ую плавку количества штейна G₁[q] последовательным обогащением сульфидной массы в ванне конвертора по меди и отработкой шлака путем задания на каждую продувку определенного количества дутья и руды, обеспечивающих практически полное удаление железа из массы в N[q]-1-ой продувке (продувке на белый матт), которое может быть выражено условием

[N[q]-1]≤ (4)

здесь - заданное по технологическим нормам содержание железа в белом матте, и получение а последней продувке (при "варке" меди) черновой меди с содержанием серы менее заданного (а⁽³⁾) по технологическим нормам, т.е.

[N[q]]-≤

с минимальным суммарным количеством меди в конверторных шлаках, слитых во всех продувках первого периода.

В этом случае формально задача распределения дутья по продувкам сводится к задаче перевода дискретного динамического объекта из заданного начального состояния (определяемого количеством, химическим составом и температурой загружаемого на первую продувку штейна) через. N[q] промежуточных стадий (продувок) с "подпиткой" процесса на них штейном в- конечное состояние, определяемое условием (4) с ограничением на траекторию процесса на (N[q] - l) -ой стадии в виде условия (5) путем задания последовательности минимизирующей критерий и удовлетворяющий ограничению:

(5)

где - количество дутья, необходимое для окисления сульфидов железа и меди, загружаемого за плавку штейна G₁[q].

Воспользуемся некоторыми технологическими особенностями процесса для упрощения постановки задачи без изменения ее сущности.

Вследствие того, что за n-ю (произвольную продувку может быть окислено не все FeS сульфидной массы, то оставшееся его количество вместе с сульфидным железом штейна, загружаемого в n+1-ой продувке), образует исходное количество FeS, подлежащее окислению в n+1 -ой продувке.

Обозначая долю окисляющегося за n-ю продувку сульфидного железа от общего количества сульфидного железа в n-ой продувке, или, что эквивалентно, долю подаваемого за n-ю продувку дутья от общего количества дутья, необходимого для окисления всего сульфидного железа, находящегося в ванне n-ой продувке; - количество дутья, эквивалентное не окислившемуся в n- ой продувке сульфидному железу, процесс распределения дутья и руды по продувкам конверторной плавки (при известном распределении штейна по продувкам) можно описать следующей системой рекуррентных уравнений:

(6)

для при следующих начальных и конечных условиях:

(7)

количество дутья на второй период определяется из условия:

(8)

и в соответствии с технологией процесса:

Здесь - количество дутья, необходимое для окисления всего сульфидного железа штейна С учетом стехиометрических соотношений реакций окисления содержания FeS в штейне и кислорода в дутье , коэффициентов потерь дутья в воздухоподводящей системе (K_Ф) и использовании кислорода в ванне конвертора можно определить из выражения

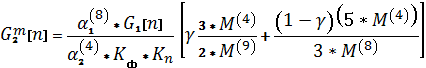(9)

для n=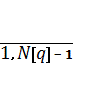

Аналогично определяем - количество дутья, необходимое для окисления всей сульфидной меди во втором периоде

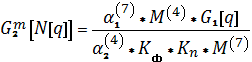(10)

где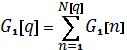

При такой форме записи процедура распределения дутья по продувкам эквивалентно замена определением последовательности , связанной с однозначной зависимостью. В этом случае упрощается задание начальных значений последовательности ими могут быть любые значения из интервала 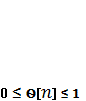, при этом выполнение условия (9) обеспечивается структурой рекуррентных уравнений (10), а выполнение условий (7) и (8) - соответственно условиям (6) и (5), но в существенно более простой форме учета при решении задачи [4].

Для компактности записи будем обозначать математическую модель процесса, описывающую изменение состояния процесса конвертирования на интервалах следующим выражением:

где - вектор переменных состояния процесса конвертирования, включающий в себя следующие компоненты:

- вектор входных переменных процесса, включающий следующие компоненты: [n];

(11)

В зависимости от конкретной задачи управления, те или иные компоненты вектора могут не использоваться при решении задачи (их значения равны нулю), а отдельные компоненты могут быть использованы в качестве управляющих (варьируемых) переменных [5].

С учетом введенных обозначений напишем математическую формулировку задачи распределением дутья по продувкам:

(12)

;

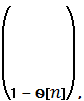
n=1, N[q]; 0≤Ѳ[n]≤1, n=

Сформулированная задача является задачей оптимального управления дискретным динамическим объектом, изменения состояния которого Х[n] под воздействием входных (управляемых и неуправляемых) воздействий W[n] описывается разностным управлением (3.1.11), начальное состояние которого задано условием Х[0]=Х₀ и [0]= 0 ограничение на изменение управляемой переменной условием 0≤Ѳ[n]≤1, конечное состояние фиксируется условиями Ѳ[N[q]-1]=1 и .

Задача определения длительности продувок конверторной плавки, описываемой разностным уравнением (11), заключается в нахождении τ[n]∀n=1,N[q] f₁ и f₂ при фиксированных значениях

полученные при решении задачи (12) и при ограничениях на температуру расплава и величину расхода дутья.

Принимая во внимание большую важность требования выполнения заданного времени плавки, введем его в математическую формулировку задачи в виде ограничения

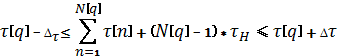
где - допустимое отклонение от заданного времени плавки;

- нормативная продолжительность операций времени слива шлака и загрузки материалов между продувками.

В таком случае, задача определения длительности продувок математически формируется в следующем виде:

(13)

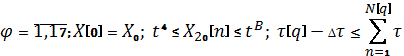[n]=‾(N[q]-1)*

где – соответственно нижнее и верхнее допустимые значения температуры расплава;

- заданное по технологии процесса значения температуры расплава;

- соответственно нижнее и верхнее допустимые значения расхода дутья.

Для решения задач рассмотренного класса широко используется методы динамического программирования и дискретного принципа максимума, а также подход, основанный на приведении исходной задачи оптимального управления к задаче математического программирования и ее решение с помощью одного из методов поиска экстремума функции многих переменных.

Сравним вычислительные затраты, необходимые при решении задачи указанными методами, поскольку именно они практической реализации разработанных алгоритмов управления.

В этом случае важными особенностями задачи, влияющими на выбор метода ее решения, являются число стадий и размерность векторов состояния и управления. Для рассматриваемой задачи число продувок (стадий) практически не превышает восьми (N≤8), состояние процесса описывается двенадцатью переменными (ξ=), размерность вектора управления равна единице (φ=1) [6].

Для приближенной оценки необходимого количества вычислений положим, что состояние процесса при использовании метода динамического программирования задается по каждой переменной на сетке с S узлами, поиск оптимального управления во всех методах производится, прямым перебором S узлов диапазона изменения управляющих переменных, поиск оптимальных начальных (или конечных) значений сопряженных переменных (или переменных состояния) при решении двухточечной граничной задачи, в случае использования принципа максимума, также осуществляется перебором на сетке с S узлами.

При сравнении затрат необходимых вычислений становится видны основные отличия методов в вычислительном плане: при применении методов динамического программирования и принципа максимума в выражении для требуемого объема вычислений в показатель степени при S входит размерность вектора состояния процесса, а в случае применения прямого метода - число стадий. Тогда становится очевидным, что для случая ξ>N рациональным является применение прямого метода для решения данного класса задач оптимального управления. Действительно, принимая величину S=10, получим 8-10¹⁺20>>8*10¹⁺⁸.

Естественно, что применяя более эффективные методы поиска, чем перебор по сетке, можно существенно сократить число необходимых вычислений: однако можно предположить, что соотношение числа необходимых вычислений для рассмотренных методов остается, примерно, тем же.

С учетом изложенных доводов, задача распределения дутья к продувкам плавки в настоящей работе решалось с использованием прямого метода, при этом задача (12), принимается во внимание нелинейность функции f₂F, формулируется как задача нелинейного программирования при наличии ограничений в виде неравенств [7].

Для решения этой задачи воспользуемся методом штрафных функций , позволяющего перейти от нахождения условного экстремума f₂ к поиску безусловного экстремума вспомогательной функции .

где (13)

здесь С-достаточно большое положительное число.

Представим ограничения задачи (14) в следующем виде:

------------------------- (14)

Тогда с учетом (12) и (13) при достаточно большом значении числа решение задачи

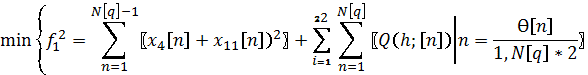
достаточно близко искомому решению задачи (12). Решение задачи (13) т.е. поиск безусловного минимума функции осуществляется с использованием метода вращающихся координат .

Вследствие того. Что алгоритм метода вращающихся координат является алгоритмом поиска, при решении задачи (14) не гарантируется нахождение глобального экстремума функции . Учитывая, однако, что начальные значения задаются по данным практики (по данным многократного решения задачи в процессе эксплуатации), можно считать, что «хорошее» начальное приближение параметра обеспечит необходимую в практических целях точность решения задачи. Результаты исследования алгоритма, проведенные, в последующем на имитационной модели в промышленных условиях подтверждают этот вывод [8].

Как видно из (12), определение длительности продувок, как и задача (14), также сводится к решению задачи нелинейного программирования с ограничениями в виде неравенства. Обозначим ограничения задачи (15) следующим образом:

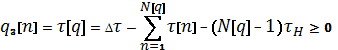
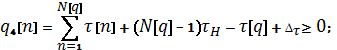
Тогда, вводя функцию аналогичную (13), преобразуем задачу (14) в задачу безусловной минимизации функции f₄ решение которой сводится к решению задачи (15) при большом достаточном значении С.

Вычисление значений

Вычисление значений

Формирование критерия

Поиск оптимальных

значений

Поиск оптимальных

значений

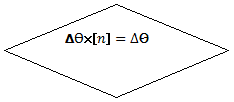
Рис. 1 - Оптимальный график плавки

+

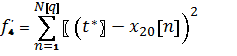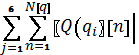
,X[0]=

Для решения задачи используется тот же поисковый алгоритм, что и для задачи.

С учетом изложенного, подхода к решению задачи формирования оптимального графика конверторной плавки разработан алгоритм, блок-схема которого приведена на рисунке 3.1. Приведем описание алгоритма в соответствии с его блок-схемой [9].

Блок 1. Вводится: коэффициенты математической модели; коэффициент распределения кислорода исходные значения заданные план графиком конверторного отделения продолжительностью плавки , количество штейна данные химических анализов заданные технологом число продувок и распределение штейна по продувкам . В соответствии с выражениями определяется значения.

Блок 2. Для заданных значений и получаемые в процессе решения задачи значений здесь τ обозначает шаг решения задачи) с использованием математической модели процесса производится вычисление значений .

Блок 3. С помощью полученных значений , выражений и формируется критерий задачи .

Блок 4. С использованием поискового алгоритма в цикле с блоками 2 и 3 определяются оптимальные значения .

Блок 5. Проверяется условие окончания поиска оптимальных значений . Если , то выполняется блок 6, в противном случае - блок 2 (здесь - шаг по переменной на r-ой итерации поиска, - предельное значение величины шага).

Блок 6. Для заданных значений W[n], значений на r-ом шаге решения с использованием математического описания процесса (3.1.11) вычисляются значения

Блок 7. С помощью полученных значений выражений и формируется критерий задачи (3.2.5).

Блок 8. С использованием поискового алгоритма в цикле с блоками 6 и 7 определяются оптимальные значения

Блок 9. Проверяется условие окончания поиска оптимальных значений . Если , , то выполняется блок 11, в противном случае -блок 7.

Блок 10. Из заданных величин и найденных и найденных формируется график конверторной плавки, который выводится на печь.

Выводы. Решение задачи управления процессом электроплавки медных концентратов сводится к определению и поддержанию оптимальных технологических режимов. Высокая размерность задачи управления, неполнота информации о состоянии процесса, различная инерционность по каналам управления объектом обуславливает целесообразность построения системы управления процессом электроплавки в классе иерархических систем управления. В данной работе включены двадцати суточные наблюдения и регистрацию входных технологических переменных: количествам химических составов загруженных гранул, оборотов флюсов, конвертерного шлака, электрической мощности и выходных: количества и химического состава штейна, отвального шлака, отходящих газов и расхода электроэнергии. Для всех переменных были определены математические ожидания, среднеквадратические отклонения.

Список использованных источников:

1. Ш.К. Кошимбаев, Войцик Вольдемар, Ж.Б. Шегебаева, Г.С.Баяндина. Постановка задач многомерного управления технологическими процессами медеплавильного производства на основе модели с оптимизацией. – Алматы: Вестник КазНТУ №5(99), 2013

2. Ш.К. Кошимбаев Оптимальное управление технологическими процессами металлургического цеха медеплавильного производства.-Алматы: Вестник КазНТУ №4, 2004

3. Новак В., Перфильева И., Мочкрож И. Математические принципы нечёткой логики = Mathematical Principles of Fuzzy Logic. — Физматлит, 2006. — 352 с. — ISBN 0-7923-8595-0

4. Рутковский Лешек Искусственные нейронные сети. Теория и практика. — М.: Горячая линия - Телеком, 2010. — 520 с.

5. Усков А. А., Кузьмин А. В. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. – М.: Горячая Линия – Телеком, 2004. – 143 с.

6. Дьяконов А. П., Круглов В. В. MATLAB. Математические пакеты расширения. Специальный справочник. СПб.: Питер, 2001. 480с (имеются главы по нечёткой логике и нейронным сетям).

7. Производство цветных металлов. – 2-е изд. Уткин Н.И. – М.: Интермет Инжиниринг, 2004. – 442с.

8. Бородин И.Ф., Судник Ю.А. Автоматизация технологических процессов. М.: Интермет Инжиниринг, 2004. – 262с.

9. Фафурин В.А. Автоматизация технологических процессов и производств. М.: Интермет Инжиниринг, 2008. – 317с.