Технические науки/3. Отраслевое машиностоение

К.т.н. Логвиненко Е.А., Николин С.А., Дудченко Д.А.

Днепропетровский национальный университет, Украина

Методика расчета параметров резонансного грохота с асимметричными колебаниями

Экспериментальные исследования резонансных грохотов, реализующих симметричные колебания, показали, что их искусственный перевод на асимметричный цикл вибрации резко увеличивает скорость движения материала на ситах, уменьшает их забиваемость клиновидными зернами, улучшает эффективность процесса рассева угля, щебня [1].

Учитывая перспективность использования асимметричного цикла колебаний и для других вибротехнологий, требующих одностороннего вибровоздействия на обрабатываемый материал, в Днепропетровском национальном университете была разработана динамическая теория нелинейных асимметричных вибросистем [2], на основе которой ниже приводится методика расчета жесткостных и динамических параметров резонансного грохота.

На рис. 1 представлена схема грохота, в которой колеблющимися массами являются короб 1 и противовес 2, соединенные между собой линейными упругими связями 3, блок-шарнирными стойками 4 и нелинейными буферными подвесками 5, имеющими асимметричную упругую характеристику. Число верхних буферов больше нижних, причем буфера разделены кронштейнами 6 короба зазорами е₁ и е₂. Для возбуждения колебаний применен кривошипно-шатунный вибровозбудитель 7, соединенный приводными упругими связями 8 с коробом. Для снижения динамических нагрузок на фундамент грохот установлен на виброизоляторы 9 небольшой жёсткости, которые практически не влияют на динамические параметры. Асимметричный цикл вибрации достигается за счет соударения разного количества верхних и нижних буферов нелинейной подвески.

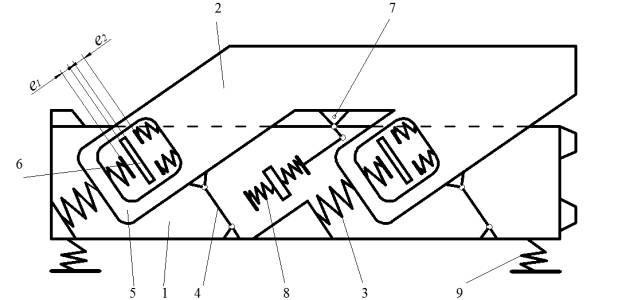Рисунок 1- Схема грохота

Расчет жесткостных и динамических параметров грохота проводится в следующем порядке.

1. При выборе исходных данных в результате конструкторской проработки определяются величины масс короба m_1, противовеса m₂ и задаются конкретные значения амплитуды короба а₁ и его несимметричных ускорений при ходе вверх W'₁ и вниз W''₁.

2. Учитывая малую жесткость опорных виброизоляторов, амплитуда противовеса

3. Относительная амплитуда масс а = а₁ + а₂

4. Эксцентриситет приводного вала ρв режиме осцилляторного резонанса необходимо принять ρ=а.

5. Учитывая динамическое смещение d противовеса вверх, целесообразно е₂ = 0, тогда d=a-Δ, где Δ- предельная деформация упругого буфера.

6. Из условия равнопрочности деформируемых на одинаковую величину верхних и нижних буферов, запишем равенство a- Δ = e₁-d = e₂+d. Отсюда e₁ = e₂ + 2d .

7. Жесткость линейных поддерживающих связей К₁ выбирается таким образом, чтобы их деформация под действием силы тяжести противовеса была несколько больше максимальной динамической деформации a_max, то есть чтобы исключалось размыкание связей

где a_max = a+d

α ‒ угол между плоскостью сита и направлением колебаний;

g ‒ ускорение свободного падения, 9,81 Н/м² .

На основе экспериментальных исследований оптимально α = 35° .

Из условия равенства потенциальной энергии в крайних положениях грохота при e₂= 0, получаем уравнение

где

K_Б1 ‒ жесткость нижних буферов;

K_Б2 ‒ жесткость верхних буферов.

8. Жесткость буферов K_Б1 и K_Б2 определяется соотношениями

где

m‒ приведенная масса системы

W_H ‒ максимальное относительное ускорение системы при движении рабочего органа вниз («нижнее» ускорение)

W_В ‒ максимальное относительное ускорение системы при движении рабочего органа вверх («верхнее» ускорение)

9. Учитывая, что деформация приводных упругих связей в осцилляторном резонансе равна нулю, определим рабочую частоту вынужденных колебаний

где

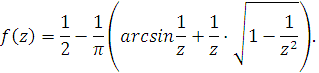
10. Жесткость приводных упругих связей

где ξ ≈1,1 ‒ коэффициент возможного изменения частоты, массы, жесткости системы.

11. Резонансная собственная частота колебаний

Численные расчеты параметра асимметричного грохота.

Исходные данные:

m₁ = 5800 кг; m₂ = 3700 кг; a₁ = 9·10^-3м; е₂= 0; W'₁=31м/с²; W''₁ =56м/с².

Результаты расчета жесткостных и динамических параметров грохота сведены в табл 1.

Таблица 1

Результаты расчета жесткостных и динамических параметров грохота

a2, м	a=ρ, м	d, м	e1, м	K1,	m,	WH,	WВ,
1	2	3	4	5	6	7	8
1,4	2,3	1,8	3,6	0,51	2260	79,6	14,38

Продолжение

KБ1,	KБ2,	z	f(z)	ν,	K0,	ω,
9	10	11	12	13	14	15
32	64,5	1,28	0,059	54,4	1,3	57,6

На основании представленных в таблице расчетов рекомендуется изготовить приводные и поддерживающие связи в виде пружин, а в качестве нелинейных связей использовать серийные резиновые буфера ГРО82-45. Так как жесткость каждого буфера составляет 8·10⁶ Н/м, то в нижней части основной подвески необходимо закрепить 4 буфера, а в верхней - 8.

Выводы. Приведенные зависимости и результаты расчета позволяют синтезировать основные характеристики грохота, реализующего заданный асимметричный закон ускорений, и могут быть использованы при расчете и выборе аналогичных параметров вибромашин иного назначения.

Литература:

1. Логвиненко Е.А. Экспериментальные исследования грохота с ассиметричным циклом колебания // Динамика и прочность тяжелых машин. ‒ 1984. ‒ С.57-61

2. Звіт про науково-дослідну роботу. Розрозробка теоретичних засад динаміки вібросистем з асиметричним циклом коливань. Дніпропетровський національний університет. Номер державної реєстрації НДР №0111U001141. ‒ Д., 2013. С-90

3. Логвиненко Е.А., Силич-Балгабаева В.Б. Динамика вибросистемы с нелинейностью ассиметричного типа в вибровозбудителе. // Вібрації в техніці та технологіях. №4(64). ‒ 2011. С.49-53